Óvalo de Cassini
En matemáticas, el óvalo de Cassini es un conjunto de puntos en un plano, de tal manera que es constante el producto de las distancias desde cada punto en el óvalo a otros dos puntos fijos y , que se encuentran a una distancia de , llamados focos de óvalo. Esta constante viene dada por . Los óvalos de Cassini llevan ese nombre por el astrónomo Giovanni Doménico Cassini.
Ecuaciones
Si los focos son (a, 0) y (−a, 0), la ecuación en forma cartesiana del óvalo de Cassini es:
La ecuación polar de los Óvalos de Cassini es:
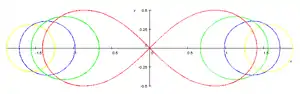
La forma del óvalo depende de la proporción e = b/a, llamada excentricidad. Cuando e > 1, el lugar geométrico es una única vuelta conectada. Si e < 1, el lugar comprende dos vueltas desconectadas. Si e = 1 la curva se denomina lemniscata de Bernoulli.
Los óvalos de Cassini se pueden considerar como secciones planas de un toro, o como curvas de nivel de una superficie de Cassini.
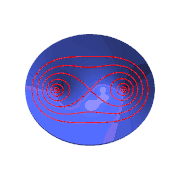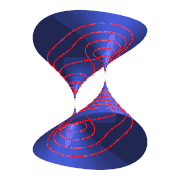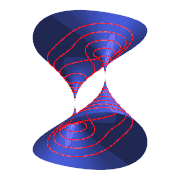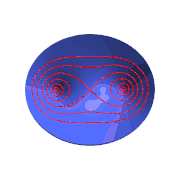 Óvalos de Cassini como curvas de nivel de una superficie de Cassini.
Óvalos de Cassini como curvas de nivel de una superficie de Cassini. Óvalos de Cassini como secciones planas de un toro.
Óvalos de Cassini como secciones planas de un toro.
Véase también
- Anexo:Lista de curvas
- Toro (geometría)
- Lemniscata
- Hipopoda
- Spira de Perseo
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Óvalo de Cassini.
Wikimedia Commons alberga una categoría multimedia sobre Óvalo de Cassini.- Hazewinkel, Michiel, ed. (2001), «Cassini oval», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
- Weisstein, Eric W. «Cassini Ovals». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.