Spira de Perseo
La spira de Perseo es un caso particular de sección tórica, en la que el plano de corte es paralelo al eje del toro (intuitivamente, una spira es cualquier sección transversal que se obtiene al cortar una rosquilla con un cuchillo verticalmente). El resultado de estas intersecciones es la familia de curvas denominadas secciones espíricas, entre las que figuran curvas como las hipopodas, los óvalos de Cassini o la lemniscata de Bernouilli.

Su ecuación cartesiana característica toma la forma general:
Su nombre deriva de la palabra griega spira, que utilizaban los antiguos griegos para referirse a la figura geométrica del toro. Fue descubierta por el geómetra de la Grecia antigua Perseo.[1][2]
Historia
Unos 200 años después de que Menecmo construyera las secciones cónicas cortando un cono con un plano, alrededor del año 150 a. C. el matemático griego Perseo investigó las curvas obtenidas al cortar un toro por un plano paralelo al eje de revolución del toro.
Geometría
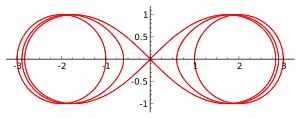
a = 1, b = 2, c = 0 (dos circunferencias)
a = 1, b = 2, c = 0.8 (dos óvalos)
a = 1, b = 2, c = 1 (lemniscata)

Notación polinómica
(En las ecuaciones de este apartado se utilizan coeficientes polinómicos, indirectamente relacionados con las dimensiones del toro).
Partiendo de la ecuación general del toro:
se intercambian y y z, de modo que el eje de revolución esté ahora en el plano xy. Tomando z = c (un plano vertical distante c del origen), se obtiene la curva de intersección, que resulta
En esta fórmula, el toro se forma girando una circunferencia de radio a con su centro siguiendo otra circunferencia de radio b (no necesariamente más grande que a, se permite la autointersección). El parámetro c es la distancia desde el plano de intersección al eje de revolución. No hay secciones espíricas con c > b + a, ya que no hay intersección; el plano queda demasiado lejos del toro para cortarlo.
Al expandir la ecuación se obtiene la forma que se ve en la definición
donde
En coordenadas polares esto se convierte en
- ; o también en:
Notación geométrica
(En las ecuaciones de este apartado se utilizan directamente como parámetros las dimensiones del toro)
La ecuación cartesiana de estas curvas viene dada por
donde r es el radio del tubo circular, R es la distancia entre el centro del tubo y el centro del toro, y c es la distancia entre el centro del toro y el plano cortante.
Dado que tanto x como y solo aparecen en la ecuación cartesiana elevados a potencias pares, estas curvas son simétricas respecto de ambos ejes coordenados (simetría par).
Según las relaciones entre R, r y c se obtienen diferentes curvas:
- Si c = 0 la curva consiste en dos circunferencias de radio r centradas en (-R, 0) y (R, 0). La ecuación cartesiana se reduce a
- Si 0 < c < R - r entonces la curva tiene dos ramas cerradas.
- Si c = R - r la curva resultante es una lemniscata. En el caso particular en el que R = 2r se obtiene la lemniscata de Bernouilli, utilizada como signo del infinito matemático desde que John Wallis ideara esta notación en 1655. La ecuación cartesiana que se obtiene así para la lemniscata de Bernouilli es
- Si R - r < c < R entonces la curva tiene solo una rama cerrada, parecida a una elipse estrechada por su parte central.
- Si R <= c < R + r la curva pierde el estrechamiento en su parte central.
- Si c = R + r la curva consiste en un único punto, denominado el origen.
- Si c > R + r la curva no tiene ningún punto.
Ejemplos de secciones espíricas
Los ejemplos incluyen la hipopoda y el óvalo de Cassini y las curvas de su familia, como la lemniscata de Bernoulli. El óvalo de Cassini tiene la notable propiedad de que el producto de las distancias a dos focos es constante. De forma homóloga, en una elipse es la suma la que es constante, en una hipérbola lo es la diferencia, y en una circunferencia es la proporción entre las dos distancias la que se conserva fija.
Véase también
Referencias
- John Stillwell: Mathematics and Its History, Springer-Verlag, 2010, ISBN 978-1-4419-6053-5, p. 33.
- Wilbur Richard Knorr:The Ancient Tradition of Geometric Problems, Dover-Publ., New York, 1993, ISBN 0-486-67532-7, p. 268 .
Enlaces externos
- O'Connor, John J.; Robertson, Edmund F., «Spiric sections» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/Curves/Spiric.html.
- Spiric Section (work in progress) de Xah Lee
- Lemniscate of Bernouilli de Xah Lee
- Weisstein, Eric W. «Lemniscate». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Scientific Symbols and Icons de Gérard P. Michon, Ph. D.