Algoritmo de Levenberg-Marquardt
En matemáticas y computación, el algoritmo de Levenberg-Marquardt (LMA o simplemente LM), también conocido como el método de mínimos cuadrados amortiguados (DLS), se utiliza para resolver problemas de mínimos cuadrados no lineales. Estos problemas de minimización surgen especialmente en el ajuste de curvas de mínimos cuadrados.
El LMA se usa en muchas aplicaciones de software para resolver problemas genéricos de ajuste de curvas. Sin embargo, como ocurre con muchos algoritmos de ajuste, el LMA solo encuentra un mínimo local, que no es necesariamente el mínimo global. El LMA interpola entre el algoritmo de Gauss-Newton (GNA) y el método de descenso de gradiente. El LMA es más robusto que el GNA, lo que significa que en muchos casos encuentra una solución incluso si comienza muy lejos del mínimo final. Para funciones de buen comportamiento y parámetros de inicio razonables, el LMA tiende a ser un poco más lento que el GNA. El LMA también se puede ver como Gauss-Newton utilizando un enfoque de región de confianza.
El algoritmo fue publicado por primera vez en 1944 por Kenneth Levenberg,[1] mientras trabajaba en el Arsenal del Ejército de Frankford. Fue redescubierto en 1963 por Donald Marquardt,[2] quien trabajó como estadístico en DuPont, e independientemente por Girard[3] Wynne[4] y Morrison.[5]
El problema
La aplicación principal del algoritmo de Levenberg-Marquardt se encuentra en el problema de ajuste de curvas de mínimos cuadrados: dado un conjunto de pares de datos empíricos ( x i , y i ) de variables independientes y dependientes, encuentre los parámetros β de la curva del modelo f ( x , β ) de modo que la suma de los cuadrados de las desviaciones S ( β ) se minimice:
- que se supone que no está vacío.
La solución
Al igual que otros algoritmos de minimización numérica, el algoritmo de Levenberg-Marquardt es un procedimiento iterativo. Para iniciar una minimización, el usuario debe proporcionar una estimación inicial del vector de parámetros β. En los casos con solo un mínimo, una conjetura estándar no informada como β T = (1, 1, ..., 1) funcionará bien; en los casos con múltiples mínimos, el algoritmo converge al mínimo global solo si la estimación inicial ya es algo cercana a la solución final.
En cada paso de iteración, el vector parámetro β se reemplaza por una nueva estimación β + δ. Para determinar δ , la función se aproxima por su linealización:
donde
es el gradiente (fila-vector en este caso) de f con respecto a β .
La suma de desviaciones cuadradas tiene su mínimo en un gradiente de cero con respecto a β . La anterior aproximación de primer orden de da
o en notación vectorial,
Tomando la derivada de con respecto a δ y establecer el resultado a cero da
donde es la matriz jacobiana, cuya fila i es igual a , y donde y son vectores con i-componente y respectivamente. Este es un conjunto de ecuaciones lineales, que se pueden resolver para δ .
La contribución de Levenberg es reemplazar esta ecuación por una "versión amortiguada":
donde I es la matriz de identidad, dando como incremento δ al vector de parámetros estimado β.
El factor de amortiguamiento (no negativo) λ se ajusta en cada iteración. Si la reducción de S es rápida, se puede usar un valor más pequeño, acercando el algoritmo al algoritmo de Gauss-Newton, mientras que si una iteración produce una reducción insuficiente del residual, λ puede aumentarse, dando un paso más cerca del descenso del gradiente dirección. Tenga en cuenta que el gradiente de S con respecto a β es igual a . Por lo tanto, para valores grandes de λ, el paso se tomará aproximadamente en la dirección del gradiente. Si la longitud del paso calculado δ o la reducción de la suma de cuadrados del último vector de parámetros β + δ cae por debajo de los límites predefinidos, la iteración se detiene, y el último vector de parámetros β se considera la solución.
Si el valor del factor de amortiguamiento λ es grande en relación con la norma de JTJ, no es necesario resolver el sistema con matriz JTJ + λI , dado que esta matriz se puede aproximar mediante λI. En este caso el algoritmo realiza una actualización en la dirección del gradiente, con un paso pequeño:
R. Fletcher proporcionó la idea de que podemos escalar cada componente del gradiente según la curvatura, de modo que haya un movimiento más grande a lo largo de las direcciones donde el gradiente es más pequeño. Esto evita la convergencia lenta en la dirección del gradiente pequeño. Por lo tanto, Fletcher en su artículo de 1971 "Una subrutina de Marquardt modificada para mínimos cuadrados no lineales", reemplazó la matriz de identidad I con la matriz diagonal que consiste en los elementos diagonales de JTJ, lo que hace que la escala de la solución sea invariante:
Un factor de amortiguación similar aparece en la regularización de Tikhonov, que se utiliza para resolver problemas lineales mal planteados, así como en la regresión de crestas, una técnica de estimación en estadística.
Elección del parámetro de amortiguación
Se han presentado varios argumentos más o menos heurísticos para la mejor opción para el parámetro de amortiguación λ. Existen argumentos teóricos que muestran por qué algunas de estas opciones garantizan la convergencia local del algoritmo; sin embargo, estas elecciones pueden hacer que la convergencia global del algoritmo sufra de las propiedades indeseables del descenso más pronunciado, en particular, una convergencia muy lenta cerca del óptimo.
Los valores absolutos de cualquier elección dependen de qué tan escalada esté el problema inicial. Marquardt recomendó comenzar con un valor λ 0 y un factor ν>1. Configurando inicialmente λ = λ0 y calculando la suma residual de cuadrados S (β) después de un paso desde el punto de inicio con el factor de amortiguamiento de λ = λ0 y en segundo lugar con λ0/ν. Si ambos de estos son peores que el punto inicial, entonces la amortiguación se incrementa por multiplicación sucesiva por ν hasta que se encuentra un punto mejor con un nuevo factor de amortiguación de λ0νk para algunos k .
Si el uso del factor de amortiguación λ / ν da como resultado una reducción en el residuo al cuadrado, esto se toma como el nuevo valor de λ (y la nueva ubicación óptima se toma como la obtenida con este factor de amortiguación) y el proceso continúa; si el uso de λ/ν resultó en un peor residuo, pero el uso de λ resultó en un mejor residual, entonces λ se mantiene sin cambios y el nuevo óptimo se toma como el valor obtenido con λ como factor de amortiguamiento.
Ejemplo

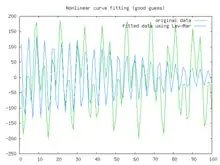
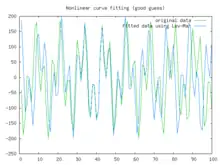
En este ejemplo tratamos de ajustar la función utilizando el algoritmo de Levenberg-Marquardt implementado en Octave GNU como la función leasqr. Las gráficas muestran una mejor adaptación progresiva para los parámetros a = 100, b = 102 utilizados en la curva inicial. Solo cuando los parámetros en el último gráfico son elegidos más cercanos al original, las curvas se ajustan exactamente. Esta ecuación es un ejemplo de condiciones iniciales muy sensibles para el algoritmo de Levenberg-Marquardt. Una de las razones de esta sensibilidad es la existencia de múltiples mínimos: la función tiene mínimos en el valor del parámetro y .
Véase también
- Región de confianza
- Método Nelder – Mead (también conocido como simplex)
- Las variantes del algoritmo de Levenberg-Marquardt también se han utilizado para resolver sistemas de ecuaciones no lineales.[6]
Referencias
- Levenberg, Kenneth (1944). «A method for the solution of certain non-linear problems in least squares». Quarterly of Applied Mathematics (en inglés) 2 (2): 164-168. ISSN 0033-569X. doi:10.1090/qam/10666.
- Marquardt, Donald W. (1 de junio de 1963). «An Algorithm for Least-Squares Estimation of Nonlinear Parameters». Journal of the Society for Industrial and Applied Mathematics 11 (2): 431-441. ISSN 0368-4245. doi:10.1137/0111030.
- Girard, André (1958). «Excerpt from Revue d'optique théorique et instrumentale». Revue d'optique théorique et instrumentale 37: 225-241, 397-424.
- Wynne, C G (1 de mayo de 1959). «Lens Designing by Electronic Digital Computer: I». Proceedings of the Physical Society (en inglés) 73 (5): 777-787. ISSN 0370-1328. doi:10.1088/0370-1328/73/5/310.
- Morrison, David (1960). «Methods for nonlinear least squares problems and convergence proofs». Proceedings of the Jet Propulsion Laboratory Seminar on Tracking Programs and Orbit Determination: 1-9.
- Christian Kanzow, Nobuo Yamashita, Masao Fukushima "Levenberg-Marquardt methods with strong local convergence properties for solving nonlinear equations with convex constraints," JCAM, 172(2):375-97, Dec. 2004, doi 10.1016/j.cam.2004.02.013.
Otras lecturas
- Moré, Jorge J.; Sorensen, Daniel C. (1983). «Computing a Trust-Region Step». SIAM J. Sci. Stat. Comput. (4): 553-572.
- Gill, Philip E.; Murray, Walter (1978). «Algorithms for the solution of the nonlinear least-squares problem». SIAM Journal on Numerical Analysis 15 (5): 977-992. doi:10.1137/0715063.
- Pujol, Jose (2007). «The solution of nonlinear inverse problems and the Levenberg-Marquardt method». Geophysics (SEG) 72 (4): W1-W16. doi:10.1190/1.2732552. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- Nocedal, Jorge; Wright, Stephen J. (2006). Numerical Optimization (2nd edición). Springer. ISBN 0-387-30303-0.
Enlaces externos
Descripciones
- Detailed description of the algorithm can be found in Numerical Recipes in C, Chapter 15.5: Nonlinear models
- C. T. Kelley, Iterative Methods for Optimization, SIAM Frontiers in Applied Mathematics, no 18, 1999, ISBN 0-89871-433-8. Online copy
- History of the algorithm in SIAM news
- A tutorial by Ananth Ranganathan
- Methods for Non-Linear Least Squares Problems by K. Madsen, H. B. Nielsen, O. Tingleff is a tutorial discussing nonlinear least-squares in general and the Levenberg–Marquardt method in particular
- T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). 2nd edition, Springer Vieweg, 2016, ISBN 978-3-658-11455-8.
- H. P. Gavin, The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems (MATLAB implementation included)
Implementaciones
Levenberg-Marquardt es un algoritmo incorporado en entornos de computación numérica SciPy, Octave GNU, Scilab, Mathematica, Matlab, NeuroSolutions, Origin, Fityk, IGOR Pro, LabVIEW y SAS. También existen numerosas bibliotecas de software que permiten utilizar el algoritmo LM en aplicaciones independientes. Algunos de ellos admiten solo la optimización básica sin restricciones, mientras que otros admiten diferentes combinaciones de restricciones de caja y lineales.
Caja e implementaciones linealmente restringidas:
- ALGLIB tiene una implementación limitada y lineal de LM mejorada en C # y C++. Algoritmo mejorado toma menos tiempo para converger y puede usar Jacobian o Hessian exacto.
- Artelys Knitro es un solucionador no lineal con una implementación del algoritmo Levenberg-Marquardt restringido por caja. Está escrito en C y tiene interfaces con C ++ / C # / Java / Python / MATLAB / R.
- ceres es una biblioteca de minimización no lineal con una implementación del algoritmo Levenberg-Marquardt restringido por cuadros. Está escrito en C ++ y usa eigen .
- IDL , el complemento MPFIT admite restricciones de cuadro.
- levmar es una implementación en C/C++ con soporte para restricciones de caja y lineales generales, distribuida bajo la Licencia Pública General de GNU .
- levmar incluye una interfaz de archivo MEX para MATLAB .
- Perl (PDL), python , Haskell y . Las interfaces NET para levmar están disponibles: vea PDL :: Fit :: Levmar o PDL :: Fit :: LM , levmar (para python) , HackageDB levmar y LevmarSharp .
- R (lenguaje de programación) tiene el paquete minpack.lm (cuadro restringido).
Implementaciones sin restricciones:
- La implementación más antigua aún en uso es lmdif , de MINPACK, en Fortran , en el dominio público . Ver también:
- lmfit , una implementación en C autocontenida del algoritmo MINPACK, con una envoltura fácil de usar para el ajuste de curvas, licencia liberal (freeBSD).
- eigen , una biblioteca de álgebra lineal de C ++, incluye una adaptación del algoritmo minpack en el módulo "NonLinearOptimization".
- La Biblioteca Científica de GNU tiene una interfaz en C para MINPACK.
- C / C ++ Minpack incluye el algoritmo de Levenberg-Marquardt.
- Python library scipy , módulo
scipy.optimize.leastsqproporciona un contenedor para las rutinas de MINPACK .
- sparseLM es una implementación de C destinada a minimizar funciones con grandes jacobianos arbitrariamente dispersos. Incluye una interfaz de MATLAB MEX. Sólo sin restricciones.
- SMarquardt.m es una rutina independiente para Matlab u Octave.
- La biblioteca InMin contiene una implementación en C ++ del algoritmo basada en la biblioteca de álgebra lineal eigen C ++. Tiene una API de lenguaje C puro, así como un enlace de Python.
- NMath tiene una implementación para NET Framework .
- gnuplot utiliza su propia implementación gnuplot.info .
- Implementaciones de lenguaje de programación Java: 1) Javanumerics , 2) Apache Commons Math , 3) finmath lib .
- OOoConv implementa el algoritmo L – M como una hoja de cálculo de OpenOffice.org Calc.
- La caja de herramientas LMAM/OLMAM Matlab implementa Levenberg-Marquardt con un impulso adaptativo para el entrenamiento de redes neuronales avanzadas.
- GADfit es una implementación de adaptación global de Fortran basada en un Levenberg-Marquardt modificado. Utiliza la diferenciación automática. Permite ajustar funciones de complejidad arbitraria, incluyendo integrales.