Algoritmo de Euclides

En matemáticas, el algoritmo de Euclides, o algoritmo euclidiano, es un método eficiente para calcular el máximo común divisor (MCD) de dos números enteros, el número más grande que los divide a ambos sin dejar resto. Lleva el nombre del antiguo matemático griego Euclides, quien lo describió por primera vez en Elementos (ca. 300 a. C.). Es un ejemplo de un algoritmo, un procedimiento paso a paso para realizar un cálculo de acuerdo con reglas bien definidas, y es uno de los algoritmos más antiguos que se siguen utilizando. Se puede usar para reducir fracciones a su forma más simple y es parte de muchos otros cálculos teórico-numéricos y criptográficos.

El algoritmo euclidiano se basa en el principio de que el máximo común divisor de dos números no cambia si el número más grande se reemplaza por su diferencia con el número más pequeño. Por ejemplo, 21 es el MCD de 252 y 105 (ya que 252 = 21 × 12 y 105 = 21 × 5), y el mismo número 21 también es el MCD de 105 y 252 − 105 = 147. Dado que este reemplazo reduce el más grande de los dos números, al repetir este proceso se obtienen pares de números sucesivamente más pequeños hasta que los dos números se vuelven iguales. Cuando eso ocurre, son el MCD de los dos números originales. Al invertir los pasos o usar el algoritmo de Euclides extendido, el MCD se puede expresar como una combinación lineal de los dos números originales, es decir, la suma de los dos números, cada uno multiplicado por un número entero (por ejemplo, 21 = 5 × 105 + (−2) × 252). El hecho de que el MCD siempre se pueda expresar de esta manera se conoce como la identidad de Bézout.

La versión del algoritmo euclidiano descrita anteriormente (y por Euclides) puede requerir muchos pasos de resta para encontrar el MCD cuando uno de los números dados es mucho más grande que el otro. Una versión más eficiente del algoritmo acorta estos pasos, en lugar de reemplazar el más grande de los dos números por su resto al dividirlo por el más pequeño de los dos (con esta versión, el algoritmo se detiene al alcanzar un resto cero). Con esta mejora, el algoritmo nunca requiere más pasos que cinco veces el número de dígitos (base 10) del número entero más pequeño. Esto fue demostrado por Gabriel Lamé en 1844 (teorema de Lamé),[1][2] y marca el comienzo de la teoría de la complejidad informática. Se desarrollaron métodos adicionales para mejorar la eficiencia del algoritmo en el siglo XX.

El algoritmo euclidiano tiene muchas aplicaciones teóricas y prácticas. Se utiliza para reducir fracciones a su forma más simple y para realizar divisiones en aritmética modular. Los cálculos que utilizan este algoritmo forman parte de los protocolos criptográficos que se usan para proteger las comunicaciones de Internet, y en los métodos para romper estos sistemas criptográficos mediante la factorización de grandes números compuestos. El algoritmo euclidiano se puede usar para resolver ecuaciones diofánticas, como encontrar números que satisfagan múltiples congruencias de acuerdo con el teorema chino del resto, para construir fracciones continuas y para encontrar aproximaciones racionales precisas a números reales. Finalmente, se puede utilizar como una herramienta básica para demostrar teoremas en la teoría de números, como el teorema de los cuatro cuadrados de Lagrange y la unicidad de las factorizaciones primas.

Algoritmo original de Euclides

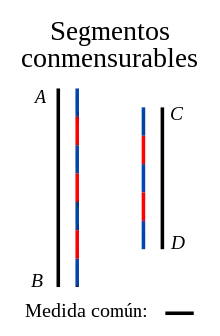
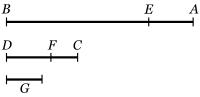
AB y CD los segmentos conmensurables.

Ejemplo del algoritmo original de Euclides.

En la concepción griega de la matemática, los números se entendían como magnitudes geométricas. Un tema recurrente en la geometría griega es el de la conmensurabilidad de dos segmentos: dos segmentos (números) AB y CD son conmensurables cuando existe un tercer segmento PQ que cabe exactamente un número entero de veces en los primeros dos; es decir, PQ «mide» (mensura: medida) a los segmentos AB y CD.

No cualquier par de segmentos es conmensurable, como encontraron los pitagóricos cuando establecen que el lado y la diagonal de un cuadrado no son conmensurables, pero en el caso de dos segmentos conmensurables se desea hallar la mayor medida común posible.

Euclides describe en la proposición VI I.2 de sus Elementos un método que permite hallar la mayor medida común posible de dos números (segmentos) que no sean primos entre sí, aunque de acuerdo a la época tal método se explica en términos geométricos, lo que se ilustra en la siguiente transcripción.

Para encontrar la máxima medida común de dos números que no sean primos entre sí.

Sean AB y CD los dos números que no son primos uno al otro. Se necesita entonces encontrar la máxima medida común de AB y CD.

Si CD mide AB entonces es una medida común puesto que CD se mide a sí mismo. Y es manifiesto que también es la mayor medida pues nada mayor a CD puede medir a CD. Pero si CD no mide a AB entonces algún número quedará de AB y CD, el menor siendo continuamente restado del mayor y que medirá al número que le precede. Porque una unidad no quedará pues si no es así, AB y CD serán primos uno del otro [Prop. VII.1], lo cual es lo contrario de lo que se supuso.

Por tanto, algún número queda que medirá el número que le precede. Y sea CD midiendo BE dejando EA menor que sí mismo y sea EA midiendo DF dejando FC menor que sí mismo y sea FC medida de AE. Entonces, como FC mide AE y AE mide DF, FC será entonces medida de DF. Y también se mide a sí mismo. Por tanto también medirá todo CD. Y CD mide a BE. Entonces CF mide a BE y también mide a EA. Así mide a todo BA y también mide a CD. Esto es, CF mide tanto a AB y CD por lo que es una medida común de AB y CD.

Afirmo que también es la mayor medida común posible porque si no lo fuera, entonces un número mayor que CF mide a los números AB y CD, sea éste G. Dado que G mide a CD y CD mide a BE, G también mide a BE. Además, mide a todo BA por lo que mide también al residuo AE. Y AE mide a DF por lo que G también mide a DF. Mide también a todo DC por lo que mide también al residuo CF, es decir el mayor mide al menor, lo cual es imposible.
Por tanto, ningún número mayor a CF puede medir a los números AB y CD. Entonces CF es la mayor medida común de AB y CD, lo cual se quería demostrar.

Euclides. Elementos VII.2

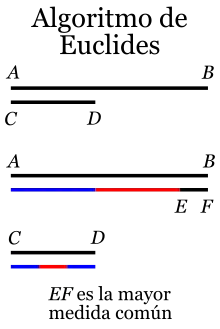
En lenguaje moderno, el algoritmo se describe como sigue:

Dados dos segmentos AB y CD (con AB>CD), restamos CD de AB tantas veces como sea posible. Si no hay residuo, entonces CD es la máxima medida común.
Si se obtiene un residuo EA, este es menor que CD y podemos repetir el proceso: restamos EA tantas veces como sea posible de CD. Si al final no queda un residuo, EA es la medida común. En caso contrario obtenemos un nuevo residuo FC menor a EA.
El proceso se repite hasta que en algún momento no se obtiene residuo. Entonces el último residuo obtenido es la mayor medida común.

El hecho de que los segmentos son conmesurables es clave para asegurar que el proceso termina tarde o temprano

Algoritmo de Euclides tradicional

Al dividir $a$ entre $b$ (números enteros), se obtiene un cociente $q$ y un resto $r$ . Es posible demostrar que el máximo común divisor de $a$ y $b$ es el mismo que el de $b$ y $r$ . Sea c el máximo común divisor de $a$ y $b$ , como $a=bq+r$ y $c$ divide a $a$ y a $b$ , divide también a $r$ . Si existiera otro número mayor que $c$ que divide a $b$ y a $r$ , también dividiría a $a$ , por lo que $c$ no sería el mcd de $a$ y $b$ , lo que contradice la hipótesis). Este es el fundamento principal del algoritmo. También es importante tener en cuenta que el máximo común divisor de cualquier número $a$ y $0$ es precisamente $a$ . Para fines prácticos, la notación $\mathrm {mcd} (a,b)$ significa máximo común divisor de $a$ y $b$ .

Según lo antes mencionado, para calcular el máximo común divisor de 2366 y 273 se puede proseguir de la siguiente manera:

Paso	Operación	Significado
1	2366 dividido entre 273 es 8 y sobran 182	$\mathrm {mcd} (2366,273)=\mathrm {mcd} (273,182)$
2	273 dividido entre 182 es 1 y sobran 91	$\mathrm {mcd} (273,182)=\mathrm {mcd} (182,91)$
3	182 dividido entre 91 es 2 y sobra 0	$\mathrm {mcd} (182,91)=\mathrm {mcd} (91,0)$

La secuencia de igualdades $\mathrm {mcd} (2366,273)=\mathrm {mcd} (273,182)=\mathrm {mcd} (182,91)=\mathrm {mcd} (91,0)$ implican que $\mathrm {mcd} (2366,273)=\mathrm {mcd} (91,0)$ . Dado que $\mathrm {mcd} (91,0)=91$ , entonces se concluye que $\mathrm {mcd} (2366,273)=91$ . Este mismo procedimiento se puede aplicar a cualesquiera dos números naturales. En general, si se desea encontrar el máximo común divisor de dos números naturales $a$ y $b$ , se siguen las siguientes reglas:

Si $b=0$ entonces $\mathrm {mcd} (a,b)=a$ y el algoritmo termina
En otro caso, $\mathrm {mcd} (a,b)=\mathrm {mcd} (b,r)$ donde $r$ es el resto de dividir $a$ entre $b$ . Para calcular $\mathrm {mcd} (b,r)$ se utilizan estas mismas reglas

Asuma que llamamos $a=r_{0}$ y $b=r_{1}$ . Aplicando estas reglas se obtiene la siguiente secuencia de operaciones:

Paso	Operación	Significado
1	$r_{0}$ dividido entre $r_{1}$ es $q_{1}$ y sobran $r_{2}$	$\mathrm {mcd} (r_{0},r_{1})=\mathrm {mcd} (r_{1},r_{2})$
2	$r_{1}$ dividido entre $r_{2}$ es $q_{2}$ y sobran $r_{3}$	$\mathrm {mcd} (r_{1},r_{2})=\mathrm {mcd} (r_{2},r_{3})$
3	$r_{2}$ dividido entre $r_{3}$ es $q_{3}$ y sobran $r_{4}$	$\mathrm {mcd} (r_{2},r_{3})=\mathrm {mcd} (r_{3},r_{4})$
$\vdots$	$\vdots$	$\vdots$
$n$	$r_{n-1}$ dividido entre $r_{n}$ es $q_{n}$ y sobran $r_{n+1}$	$\mathrm {mcd} (r_{n-1},r_{n})=\mathrm {mcd} (r_{n},r_{n+1})$
$n+1$	$r_{n}$ dividido entre $r_{n+1}$ es $q_{n+1}$ y sobra $0$	$\mathrm {mcd} (r_{n},r_{n+1})=\mathrm {mcd} (r_{n+1},0)$

Como la sucesión de residuos va disminuyendo, al final un residuo tiene que ser cero y es en ese momento cuando el algoritmo termina. El máximo común divisor es precisamente $r_{n+1}$ (el último residuo que no es cero).

Generalización

En realidad, el algoritmo de Euclides funciona no sólo para los números naturales, sino para cualquier elemento en el que exista una "división con residuo". A este tipo de divisiones se les llama divisiones euclidianas y a los conjuntos donde se puede definir dicha división se les llama dominios euclídeos. Por ejemplo, el conjunto de los números enteros y el de los polinomios con coeficientes racionales son dominios euclídeos porque podemos definir una división con residuo (véase División polinomial). De esta manera, se puede calcular el máximo común divisor de dos números enteros o de dos polinomios.

Por ejemplo, para calcular el máximo común divisor de los polinomios $P(x)=x^{5}+2x^{3}+x$ y $Q(x)=x^{4}-1$ el algoritmo de Euclides sugiere la siguiente secuencia de operaciones:

Paso	Operación	Significado
1	$x^{5}+2x^{3}+x$ dividido entre $x^{4}-1$ es $x$ y sobra $2x^{3}+2x$	$\mathrm {mcd} (x^{5}+2x^{3}+x,x^{4}-1)=\mathrm {mcd} (x^{4}-1,2x^{3}+2x)$
2	$x^{4}-1$ dividido entre $2x^{3}+2x$ es $\textstyle {{\frac {1}{2}}x}$ y sobra $-x^{2}-1$	$\mathrm {mcd} (x^{4}-1,2x^{3}+2x)=\mathrm {mcd} (2x^{3}+2x,-x^{2}-1)$
3	$2x^{3}+2x$ dividido entre $-x^{2}-1$ es $-2x$ y sobra 0	$\mathrm {mcd} (2x^{3}+2x,-x^{2}-1)=\mathrm {mcd} (-x^{2}-1,0)$

De esta manera se concluye que su máximo común divisor es $-x^{2}-1$ .

Descripción formal

Se puede expresar este algoritmo de manera más formal usando pseudocódigo. En este caso la expresión " $x\;{\bmod {\;}}y$ " significa "el residuo de dividir $x$ entre $y$ " (véase Aritmética modular).

Algoritmo 1 de Euclides
Entrada: Valores $a$ y $b$ pertenecientes a un dominio euclídeo Salida: Un máximo común divisor de $a$ y $b$ $r_{0}\gets a$ , $r_{1}\gets b$ $i\gets 1$ Mientras $r_{i}\neq 0$ haga lo siguiente: $r_{i+1}\gets r_{i-1}\;{\bmod {\;}}r_{i}$ $i\gets i+1$ El resultado es: $r_{i-1}$

Vale la pena notar que este algoritmo no es eficiente ser implementado directamente en una computadora, ya que requeriría memorizar todos los valores de $r_{i}$ .

Algoritmo de Euclides extendido

El algoritmo de Euclides extendido permite, además de encontrar un máximo común divisor de dos números enteros $a$ y $b$ , expresarlo como la mínima combinación lineal de esos números, es decir, encontrar números enteros $s$ y $t$ tales que $\mathrm {mcd} (a,b)=as+bt$ . Esto se generaliza también hacia cualquier dominio euclidiano.

Fundamentos

Existen varias maneras de explicar el algoritmo de Euclides extendido, una de las más comunes consiste en la siguiente:

Usar el algoritmo tradicional de Euclides. En cada paso, en lugar de " $a$ dividido entre $b$ es $q$ y de resto $r$ " se escribe la ecuación $a=bq+r$ (véase algoritmo de la división).
Se despeja el resto de cada ecuación.
Se sustituye el resto de la última ecuación en la penúltima, y la penúltima en la antepenúltima y así sucesivamente hasta llegar a la primera ecuación, y en todo paso se expresa cada resto como combinación lineal.

Sin embargo, en aras de la comprensión y memorización de este algoritmo, es conveniente conocer la siguiente caracterización. Para multiplicar dos matrices de tamaño $2\times 2$ se usa la siguiente fórmula (véase Producto de matrices):

(1) ${\begin{bmatrix}e&f\\g&h\end{bmatrix}}\times {\begin{bmatrix}a&b\\c&d\end{bmatrix}}={\begin{bmatrix}ea+fc&eb+fd\\ga+hc&gb+hd\end{bmatrix}}$

Supóngase que se utiliza el algoritmo de Euclides tradicional para calcular los valores $q_{i}$ y $r_{i}$ que ahí se describen. Por cada valor $q_{i}$ calculado se puede formar la matriz $\textstyle Q_{i}={\begin{bmatrix}0&1\\1&-q_{i}\end{bmatrix}}$ . Usando la ecuación (1) de manera repetida se puede calcular el producto de las primeras $i$ matrices de este tipo:

${\begin{bmatrix}s_{i}&t_{i}\\s_{i+1}&t_{i+1}\end{bmatrix}}={\begin{bmatrix}0&1\\1&-q_{i}\end{bmatrix}}\times {\begin{bmatrix}0&1\\1&-q_{i-1}\end{bmatrix}}\times \cdots \times {\begin{bmatrix}0&1\\1&-q_{1}\end{bmatrix}}$

Resulta ser que los valores $s_{i}$ y $t_{i}$ tienen la propiedad de que $r_{i}=as_{i}+bt_{i}$ , es decir, expresan a $r_{i}$ como una combinación lineal de $a$ y $b$ . Particularmente, como $\mathrm {mcd} (a,b)=r_{n+1}$ entonces se tiene $\mathrm {mcd} (a,b)=as_{n+1}+bt_{n+1}$ , lo cual es la solución del problema. Esta propiedad no debería ser sorprendente, pues esta multiplicación de matrices equivale al método antes descrito donde se substituye cada ecuación en la anterior. Es importante calcular $Q_{i}\times \cdots \times Q_{3}\times Q_{2}\times Q_{1}$ en ese mismo orden. La matriz $Q_{1}$ aparece en el extremo derecho y la matriz $Q_{i}$ en el izquierdo.

Regresando al primer ejemplo, la sucesión de cocientes es $q_{1}=8$ , $q_{2}=1$ y $q_{3}=2$ . Entonces se puede calcular

${\begin{bmatrix}-1&9\\3&-26\end{bmatrix}}={\begin{bmatrix}0&1\\1&-2\end{bmatrix}}\times {\begin{bmatrix}0&1\\1&-1\end{bmatrix}}\times {\begin{bmatrix}0&1\\1&-8\end{bmatrix}}$

Utilizando el primer renglón de esta matriz se puede leer que $91=2366(-1)+273(9)$ , es decir, se ha encontrado la manera de expresar al máximo común divisor de 2366 y 273 como una combinación lineal.

Descripción formal

Para expresar el algoritmo de Euclides extendido es conveniente notar la manera en que se calculan los valores $s_{i}$ y $t_{i}$ con la multiplicación de matrices:

${\begin{bmatrix}s_{i}&t_{i}\\s_{i+1}&t_{i+1}\end{bmatrix}}={\begin{bmatrix}s_{i}&t_{i}\\s_{i-1}-q_{i}s_{i}&t_{i-1}-q_{i}t_{i}\end{bmatrix}}={\begin{bmatrix}0&1\\1&-q_{i}\end{bmatrix}}\times {\begin{bmatrix}s_{i-1}&t_{i-1}\\s_{i}&t_{i}\end{bmatrix}}$

De esta manera $s_{i+1}=s_{i-1}-q_{i}s_{i}$ y además $t_{i+1}=t_{i-1}-q_{i}t_{i}$ . Por lo tanto el algoritmo en pseudocódigo se puede expresar como sigue:

Algoritmo 2 de Euclides extendido
Entrada: Valores $a$ y $b$ pertenecientes a un dominio euclídeo Salida: Un máximo común divisor de $a$ y $b$ , y valores $s$ y $t$ tales que $\mathrm {mcd} (a,b)=as+bt$ $r_{0}\gets a,r_{1}\gets b,s_{0}\gets 1,t_{0}\gets 0,s_{1}\gets 0,t_{1}\gets 1$ $i\gets 1$ Mientras $r_{i}\neq 0$ haga lo siguiente: Divida $r_{i-1}$ entre $r_{i}$ para obtener el cociente $q_{i}$ y el residuo $r_{i+1}$ $s_{i+1}\gets s_{i-1}-q_{i}s_{i}$ $t_{i+1}\gets t_{i-1}-q_{i}t_{i}$ $i\gets i+1$ El resultado es: $r_{i-1}$ es un máximo común divisor de $a$ y $b$ y se expresa $r_{i-1}=as_{i-1}+bt_{i-1}$

Aplicaciones

Simplificar fracciones

Al momento de hacer cálculos con fracciones, es de gran importancia saber cómo simplificarlas. Por ejemplo, la fracción $\textstyle {\frac {65}{91}}$ es equivalente con $\textstyle {\frac {5}{7}}$ (véase Número racional). De manera más general, $\textstyle {\frac {a}{b}}={\frac {ca}{cb}}$ siempre que $c\neq 0$ . Para reducir una fracción cualquiera $\textstyle {\frac {a}{b}}$ , sólo se necesita dividir $a$ y $b$ entre su máximo común divisor.

Por ejemplo, si se desea reducir $\textstyle {\frac {166}{249}}$ , primero se usa el algoritmo de Euclides para encontrar $\mathrm {mcd} (166,249)=83$ . Se hacen las divisiones $\textstyle 166\div 83=2$ y $\textstyle 249\div 83=3$ . Luego entonces se concluye que $\textstyle {\frac {166}{249}}={\frac {2}{3}}$ .

Fracciones continuas

La sucesión de divisiones que se efectúan al seguir el algoritmo de Euclides puede ser utilizada para expresar una fracción cualquiera $\textstyle {\frac {a}{b}}$ como fracción continua. Esto se debe a que si $a=bq+r$ y $r\neq 0$ , entonces

(3) ${\frac {a}{b}}=q+{\frac {1}{\frac {b}{r}}}$

Por ejemplo, para encontrar el máximo común divisor de $93164$ y $5826$ el algoritmo genera la siguiente secuencia de divisiones:

Paso	Operación	Significado
1	93164 dividido entre 5826 es 15 y sobran 5774	$93164=5826\times 15+5774$
2	5826 dividido entre 5774 es 1 y sobran 52	$5826=5774\times 1+52$
3	5774 dividido entre 52 es 111 y sobran 2	$5774=52\times 111+2$
4	52 dividido entre 2 es 26 y sobra 0	$52=2\times 26+0$

Todas estas ecuaciones las podemos hacer parecidas a la ecuación (3 3):

$\textstyle {\frac {93164}{5826}}=15+{\frac {1}{\frac {5826}{5774}}}$
$\textstyle {\frac {5826}{5774}}=1+{\frac {1}{\frac {5774}{52}}}$
$\textstyle {\frac {5774}{52}}=111+{\frac {1}{\frac {52}{2}}}$
$\textstyle {\frac {52}{2}}=26$

Si se sustituye la segunda ecuación en la primera, se obtiene

${\frac {93164}{5826}}=15+{\frac {1}{1+{\frac {1}{\frac {5774}{52}}}}}$

Si se repite este proceso de substitución entonces se obtiene la expresión deseada:

${\frac {93164}{5826}}=15+{\frac {1}{1+{\frac {1}{111+{\frac {1}{26}}}}}}$

De manera más general, la fracción continua encontrada con este algoritmo siempre es de la forma

${\frac {a}{b}}=q_{1}+{\frac {1}{q_{2}+{\frac {1}{q_{3}+{\frac {1}{\ddots q_{n-1}+{\frac {1}{q_{n}}}}}}}}}$

Inversos módulo m

Decimos que dos números enteros son congruentes módulo $m$ (aunque también se puede generalizar para cualquier otro dominio euclídeo) si al dividirlos entre $m$ obtenemos el mismo residuo (véase Congruencia). Por ejemplo, 7 es congruente con 12 módulo 5 porque al dividir 7 entre 5 y 12 entre 5, en ambos casos obtenemos el mismo residuo (que es 2). Cuando $a$ es congruente con $b$ módulo $m$ se escribe $a\equiv b{\pmod {m}}$ , en el ejemplo anterior se tiene $7\equiv 12{\pmod {5}}$ . Supóngase que se conocen los valores de $a$ , $b$ y $m$ , pero que se desconoce el valor $x$ en la siguiente congruencia:

(2) $ax\equiv b{\pmod {m}}$

Basta encontrar un valor $a^{-1}$ que satisfaga: $a^{-1}a\equiv 1{\pmod {m}}$ , pues de esta manera al multiplicar la ecuación (2) por $a^{-1}$ se tendrá la solución deseada:

$x\equiv a^{-1}b{\pmod {m}}$

Al elemento $a^{-1}$ se le llama "inverso módulo $m$ " de $a$ . Desafortunadamente este valor no siempre existe. Por ejemplo, con $a=4$ y $m=6$ no existe ningún número entero $a^{-1}$ tal que $a^{-1}4\equiv 1{\pmod {6}}$ . De hecho este valor existe si y sólo si $\mathrm {mcd} (a,m)=1$ (la existencia de soluciones depende de la condición $\mathrm {mcd} (a,m)|b$ , mientras que la unicidad depende de que el $\mathrm {mcd} (a,m)=1$ ). Más aún, si al usar el algoritmo de Euclides extendido (ahora con $b=m$ ) se obtiene $1=as+mt$ , entonces el valor $s$ es el inverso módulo $m$ de $a$ . Por ejemplo, se desea resolver la ecuación

$5x\equiv 2{\pmod {9}}$

Entonces con el algoritmo de Euclides extendido se obtiene que $\mathrm {mcd} (5,9)=1=5(2)+9(-1)$ . Como $\mathrm {mcd} (5,9)=1$ entonces 5 tiene un inverso módulo $9$ . Más aún, como $1=5(2)+9(-1)$ , entonces ese inverso es 2. Entonces

$x\equiv 2(2){\pmod {9}}$

Es decir que el valor de $x$ es $4$ .

Complejidad del algoritmo

Gráfica del número de divisiones efectuadas en el algoritmo de Euclides. El rojo indica pocas operaciones, mientras que los colores más azules representan mayor número de operaciones.

El teorema de Lamé afirma que el caso peor para este algoritmo es cuando se le pide calcular el máximo común divisor de dos números consecutivos de la sucesión de Fibonacci. Por ejemplo, si se desea calcular el máximo común divisor de $f_{10}=55$ y $f_{11}=89$ se obtiene la siguiente secuencia de operaciones:

Paso	Operación	Significado
1	89 dividido entre 55 es 1 y sobran 34	$\mathrm {mcd} (89,55)=\mathrm {mcd} (55,34)$
2	55 dividido entre 34 es 1 y sobran 21	$\mathrm {mcd} (55,34)=\mathrm {mcd} (34,21)$
3	34 dividido entre 21 es 1 y sobran 13	$\mathrm {mcd} (34,21)=\mathrm {mcd} (21,13)$
4	21 dividido entre 13 es 1 y sobran 8	$\mathrm {mcd} (21,13)=\mathrm {mcd} (13,8)$
5	13 dividido entre 8 es 1 y sobran 5	$\mathrm {mcd} (13,8)=\mathrm {mcd} (8,5)$
6	8 dividido entre 5 es 1 y sobran 3	$\mathrm {mcd} (8,5)=\mathrm {mcd} (5,3)$
7	5 dividido entre 3 es 1 y sobran 2	$\mathrm {mcd} (5,3)=\mathrm {mcd} (3,2)$
8	3 dividido entre 2 es 1 y sobran 1	$\mathrm {mcd} (3,2)=\mathrm {mcd} (2,1)$
9	2 dividido entre 1 es 2 y sobra 0	$\mathrm {mcd} (2,1)=\mathrm {mcd} (1,0)$

En este ejemplo se observa que con estos dos números de dos dígitos decimales, se necesita hacer 9 divisiones. En general, el número de divisiones efectuadas por el algoritmo nunca supera 5 veces el número de dígitos que tienen estos números. En términos de complejidad computacional, esto significa que se requieren $O(\log n)$ divisiones para calcular el máximo común divisor de $n$ y $m$ donde $n>m$ .

El número promedio de divisiones efectuadas por el algoritmo se estuvo investigando desde 1968, pero solo hasta apenas el año 2002, Brigitte Vallée demostró que si los dos números se pueden representar con $n$ bits, entonces el número promedio de divisiones necesarias es $\textstyle {{\frac {\pi ^{2}}{6}}n}$ .

Sin embargo, no basta con saber el número de divisiones. Hay que recordar que el algoritmo de Euclides funciona tanto para polinomios como para números enteros, y en general, cualquier dominio Euclídeo. En cada caso, la complejidad del algoritmo depende del número de divisiones efectuadas y del costo de cada división. En el caso de los polinomios, el número de divisiones es $O(\log n)$ donde $n$ es el grado de los polinomios.

Implementación en pseudocódigo

En general, los algoritmos 1 y 2 no son muy apropiados para implementarse directamente en un lenguaje de programación, especialmente porque consumen mucha memoria. Si no se necesitan los valores intermedios, y sólo se desea calcular el máximo común divisor de dos números enteros, conviene usar estas variantes:

Algoritmo de Euclides tradicional implementado de manera recurrente
Función $\mathrm {mcd} (a,b)$ : Si $b=0$ entonces: El resultado es $a$ En otro caso: El resultado es $\mathrm {mcd} (b,a\;{\bmod {\;}}b)$

Algoritmo de Euclides tradicional implementado de manera iterativa
Función $\mathrm {mcd} (a,b)$ : Mientras $b\neq 0$ haga lo siguiente: $(a,b)\gets (b,a\;{\bmod {\;}}b)$ El resultado es $a$

Algoritmo de Euclides extendido implementado de manera recurrente
Función ${\rm {Euclides}}(a,b)$ : Si $b=0$ entonces: El resultado es $(a,1,0)$ En otro caso: $(d,s,t)\gets {\rm {Euclides}}(b,a\;{\bmod {\;}}b)$ El resultado es $(d,t,s-(a\div b)t)$

Algoritmo de Euclides extendido implementado de manera iterativa
Función ${\rm {Euclides}}(a,b)$ : $(s,t,s^{\prime },t^{\prime })\gets (1,0,0,1)$ Mientras $b\neq 0$ haga lo siguiente: Divida $a$ entre $b$ para obtener un cociente $q$ y un residuo $r$ $(a,s,t,b,s^{\prime },t^{\prime })\gets (b,s^{\prime },t^{\prime },r,s-s^{\prime }q,t-t^{\prime }q)$ El resultado es $(a,s,t)$

Algoritmo de Euclides extendido implementado de manera iterativa con matrices
Función ${\rm {Euclides}}(a,b)$ : $Q\gets {\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ Mientras $b\neq 0$ haga lo siguiente: Divida $a$ entre $b$ para obtener un cociente $q$ y un residuo $r$ $Q\gets {\begin{pmatrix}0&1\\1&-q\end{pmatrix}}\times Q$ $(a,b)\gets (b,r)$ El resultado es $(a,Q_{11},Q_{12})$

Acerca de la notación empleada:

$x\gets y$ significa "asigne a la variable $x$ el valor actual de $y$ ". En lenguajes como C, Java, C#, Python y Visual Basic esto significa simplemente x = y. En otros lenguajes como Pascal se traduce en a := b, en Maxima es a : b, en R, S y Ocaml es x <- y, e inclusive se utiliza la flecha x ← y como el caso de APL.
$(x,y,z)\gets (a,b,c)$ significa que primero se evalúan los valores $a,b,c$ y luego se asigna $x\gets a,y\gets b,z\gets c$ , etc. En lenguajes como Python, Ruby o Maxima esta instrucción tiene una estructura muy similar, como por ejemplo en Python: (x,y,z) = (a,b,c). En otros lenguajes es necesario el uso de variables auxiliares, como por ejemplo en lenguaje C: aux1 = b; aux2 = c; x = a; y = aux1; z = aux2;.
$a\div b$ significa "el cociente de dividir $a$ entre $b$ ". A esta operación se le conoce también como la división truncada porque trunca la parte fraccionaria del número. En muchos lenguajes de programación esto se implementa simplemente como a/b. Otras maneras son a\b (Visual Basic) , a div b (Pascal) o bien a//b (Python 3).
$a\;{\bmod {\;}}b$ significa "el residuo de dividir $a$ entre $b$ ". A esta operación se le conoce simplemente como módulo. En muchos lenguajes de programación se implementa como a % b, mientras que en otros es a mod b (Visual Basic o Pascal) o bien a rem b (Ada).

Véase también

Implementaciones en lenguajes en la parte de discusión

Referencias

Lamé, Gabriel (1844). «Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers». Actas de las sesiones de la Academia de Ciencias (en francés) 19: 867-870.
Ballester Niebla, Claudia (2017). Números primos. Algunas cuestiones históricas, polinomios ciclotómicos y tests de primalidad.. Universidad de La Laguna. Consultado el 4 de julio de 2023.

Bibliografía

von zur Gathen, Joachim; Gerhard, Jürgen (2003). «The Euclidean Algorithm». Modern Computer Algebra. Cambridge University Press. ISBN 0-521-82646-2.
Shoup, Victor (2008). «Euclid’s algorithm». A Computational Introduction to Number Theory and Algebra. Cambridge University Press. ISBN 978-0-521-85154-1.
Johnsonbaugh, Richard (2005). «Introducción a la teoría de números». Matemáticas Discretas. México: PEARSON EDUCACIÓN. ISBN 970-26-0637-3.
Ralph P. Grimaldi (1998). «Propiedades de los números enteros: Inducción matemática». Matemáticas Discreta y Combinatoria. México: Addison Wesley Longman de México. ISBN 968-444-324-2.
Lipschutz, Seymour; Lipson, Marc (2009). «Propiedades de los enteros». Matemáticas Discretas. McGraw-Hill. ISBN 978-970-10-7236-3.
Brassard, Gilles; Bratley, Paul (1997). «Análisis de algoritmos». Fundamentos de Algoritmia. Madrid: PRENTICE HALL. ISBN 84-89660-00-X.
Vallée, Brigitte (2002). «Dynamical Analysis of $\alpha$ -Euclidean Algorithms». Journal of Algorithms 44 (1). ISSN 0196-6774 , pp. 246-285. Archivado desde el original el 2 de octubre de 2006.
Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford (2009). «Number-Theoretic Algorithms». Introduction to Algorithms. The MIT Press. ISBN 978-0-262-53305-8.
Barrera Mora, Fernando (2005). «Definiciones y resultados generales». Introducción a la Teoría de Grupos. Publicaciones Electrónicas de la Sociedad Matemática Mexicana. p. 16-17. ISBN 968-9161-02-4. Consultado el 2 de julio de 2017.
Cárdenas, Humberto; Lluis, Emilio; Raggi, Francisco; Tomás, Francisco (2004). «Divisibilidad». Álgebra Superior. México: Trillas. ISBN 968-24-3783-0.
Pérez Seguí, María Luisa (2006). «Divisibilidad». Teoría de Números. Instituto de Matemáticas, UNAM. ISBN 970-32-1170-0.
Sánchez Velázquez, Jesús (1998). «Algoritmos para números grandes». Introducción al análisis de algoritmos. México: Trillas. ISBN 968-24-4341-5.
Baldor, Aurelio (2008). «Máximo común divisor». Álgebra. México: Grupo Editorial Patria. ISBN 978-970-817-000-0.

Enlaces externos

Wikilibros alberga un libro o manual sobre implementaciones del algoritmo de Euclides.
Divisibilidad. El algoritmo de Euclides.
Algoritmo de Euclides.
Weisstein, Eric W. «Euclidean Algorithm». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Explicación dinámica del máximo común divisor en este vídeo de YouTube.
En gaussianos se pueden ver explicaciones y ejemplos un poco más avanzados de este algoritmo.

Datos: Q230848
Multimedia: Euclidean algorithm / Q230848

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Lamé, Gabriel (1844). «Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers». Actas de las sesiones de la Academia de Ciencias (en francés) 19: 867-870.

[2] Ballester Niebla, Claudia (2017). Números primos. Algunas cuestiones históricas, polinomios ciclotómicos y tests de primalidad.. Universidad de La Laguna. Consultado el 4 de julio de 2023.