Apolonio de Perge
Apolonio de Perge o Perga (en griego Ἀπολλώνιος) (Perge, c. 262 a. C. - Alejandría, c. 190 a. C.)[1] fue un matemático y astrónomo griego famoso por su obra Sobre las secciones cónicas. Él fue quien dio el nombre de elipse, parábola e hipérbola, a las figuras que conocemos. Logró solucionar la ecuación general de segundo grado por medio de la geometría cónica.[2]
| Apolonio de Perga (Griego antiguo: Ἀπολλώνιος) | ||
|---|---|---|
 Detalle de una obra de 1537 representanto a Apolonio de Perge | ||
| Información personal | ||
| Nombre en griego antiguo | Ἀπολλώνιος ὁ Περγαῖος | |
| Nacimiento |
262 a. C. Perge | |
| Fallecimiento |
190 a. C. (72 años) Alejandría | |
| Información profesional | ||
| Área | Matemático y Astrónomo | |
| Conocido por |
Teoría de los epiciclos Problema de Apolonio | |

También se le atribuye la hipótesis de las órbitas excéntricas o teoría de los epiciclos para intentar explicar el movimiento aparente de los planetas y de la velocidad variable de la Luna.
Sus extensos trabajos sobre geometría tratan de las secciones cónicas y de las curvas planas y la cuadratura de sus áreas.[3] Recopiló su obra en ocho libros y fue conocido con el sobrenombre de El Gran Geómetra.[4]
Biografía
Nació alrededor del 262 a. C. en la ciudad de Perge o Perga (Turquía) y falleció alrededor del 190 a. C. en Alejandría, Egipto.
Se sabe que permaneció en la ciudad de Perge durante los reinados de Ptolomeo Evergetes y Ptolomeo Filopátor, a la vez que fue tesorero general de Ptolomeo Filadelfo. Por las fuentes se puede afirmar que era entre veinticinco y cuarenta años más joven que Arquímedes, de ahí la estimación de sus años de nacimiento y muerte. Aparte de eso, lo poco que se sabe de su vida es que estudió en Alejandría y en esta ciudad se dedicó a la enseñanza.
Obra
Apolonio estudió las secciones cónicas utilizando como herramienta las proporciones, relacionando las magnitudes de cada elemento que conforman cada sección cónica en el caso de la parábola, elipse e hipérbola donde utilizó este método para definir las propiedades de cada corte con el cono, como lo demuestra Heath (1896), además propuso y resolvió el problema de hallar las circunferencias tangentes a tres círculos dados, conocido como problema de Apolonio. El problema aparece en su obra, hoy perdida, Las Tangencias o Los Contactos, conocida gracias a Pappus de Alejandría. Respecto a sus obras, se han perdido muchas:
- Reparto rápido (Ὠκυτόκιον), en el que se enseñaban métodos rápidos de cálculo y se daba una aproximación del número π.
- Secciones en una razón dada (Λόγου ἀποτομή, De Rationis Sectione) , trataba sobre los problemas derivados de trazar una recta que pase por un punto dado y que corte a otras dos rectas dadas en segmentos (medidos desde sendos puntos situados en dichas rectas) que estén en una razón dada (este problema es equivalente a resolver la ecuación).
- Secciones en un área dada (Χωρίου ἀποτομή, De Spatii Sectione), problema parecido al anterior, pero ahora se pide que los segmentos determinados por las intersecciones formen un rectángulo equivalente a otro (este problema es equivalente a resolver la ecuación).
- Secciones determinadas (Διωρισμένη τομή, De Sectione Determinata), dados cuatro puntos A, B, C, D, sobre una recta, encontrar un quinto punto P, tal que el rectángulo construido sobre AP y CP esté en una razón dada con el rectángulo construido sobre BP y DP.
- Tangencias (Ἐπαφαί, De Tactionibus), resuelve los problemas de construir una circunferencia tangente a tres elementos cualesquiera elegidos entre un punto, una recta y una circunferencia (este problema se conoce como el problema de Apolonio).
- Lugares planos (Τόποι ἐπίπεδοι, De Locis Planis), los griegos clasificaban las curvas en tres tipos: lugares planos, eran las rectas y las circunferencias, lugares sólidos eran las secciones cónicas y lugares lineales el resto de las curvas; Inclinaciones, trataba del problema de trazar una circunferencia dada una cuerda de longitud dada pasando por un punto dado.

Solo dos obras de Apolonio han llegado hasta nuestros días: Secciones en una razón dada (no se conserva el original sino una traducción al árabe) y Las Cónicas (únicamente se conserva el original de la mitad de la obra, el resto es una traducción al árabe). Esta última es la obra más importante de Apolonio, es más, junto con los Elementos de Euclides es uno de los libros más importantes de matemáticas.

Las Cónicas está formado por 8 libros.[5] Fue escrito cuando Apolonio estaba en Alejandría pero posteriormente, ya en Pérgamo (hoy Bergama en Turquía), lo mejoró.
- El libro I: trata de las propiedades fundamentales de estas curvas.
- El libro II trata de los diámetros conjugados y de las tangentes de estas curvas.
- El libro III: trata de los tipos de conos.
- El libro IV: trata de las maneras en que pueden cortarse las secciones de conos.
- El libro V: estudia segmentos máximos y mínimos trazados respecto a una cónica.
- El libro VI: trata sobre cónicas semejantes.
- El libro VII: trata sobre los diámetros conjugados.
- El libro VIII: se ha perdido, se cree que era un apéndice.
Los métodos que utiliza Apolonio (uso de rectas como sistemas de referencia) son muy parecidos a los utilizados por Descartes en su Geometría y se considera una anticipación de la Geometría analítica actual. De hecho ya utilizaba las coordenadas rectangulares. Con ayuda de estas, Apolonio definió curvas que eran bien conocidas en su tiempo: la parábola, la hipérbola y la elipse mediante las ecuaciones:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle y^2 = p \cdot x } ( parábola)
- (hipérbola)
- (elipse)
- donde p y a son números positivos .[6]
Obras documentadas de Apolonio
Apolonio fue un geómetra prolífico, con un gran número de obras. Sólo se conserva una, Cónicas. De los ocho libros que la componen, sólo los cuatro primeros pueden considerarse verosímiles a partir de los textos originales de Apolonio. Los libros 5-7 sólo están disponibles en una traducción árabe de Thābit ibn Qurra encargada por los Banū Mūsā. El original griego se ha perdido.[7] Se desconoce el estado del Libro VIII. Existió un primer borrador. Se desconoce si se llegó a producir el borrador final. Existe una "reconstrucción" de Edmond Halley en latín. No hay manera de saber cuánto de él, si es que hay algo, se parece a Apolonio. Halley también reconstruyó De Rationis Sectione y De Spatii Sectione. Más allá de estas obras, salvo un puñado de fragmentos, termina la documentación que de algún modo podría interpretarse como descendiente de Apolonio.
Muchas de las obras perdidas son descritas o mencionadas por comentaristas. Además, hay ideas atribuidas a Apolonio por otros autores sin documentación. Creíbles o no, son rumores. Algunos autores identifican a Apolonio como autor de ciertas ideas, a las que por consiguiente se da su nombre. Otros intentan expresar a Apolonio en notación o fraseología moderna con grados indeterminados de fidelidad.
Cónicas
El texto griego de Cónicas utiliza la disposición de Euclidesa de definiciones, figuras y sus partes; es decir, los "dados", seguidos de proposiciones "a demostrar". Los libros I-VII presentan 387 proposiciones. Este tipo de disposición puede verse en cualquier libro de texto moderno de geometría de la materia tradicional. Como en cualquier curso de matemáticas, el material es muy denso y su estudio, necesariamente lento. Apolonio tenía un plan para cada libro, que se describe en parte en los Prefacios. Los epígrafes, o indicadores del plan, son algo deficitarios, ya que Apolonio se ha basado más en el flujo lógico de los temas.
Se crea así un nicho intelectual para los comentaristas de todas las épocas. Cada uno debe presentar a Apolonio de la manera más lúcida y pertinente para su época. Utilizan diversos métodos: anotaciones, amplio material de introducción, diferentes formatos, dibujos adicionales, reorganización superficial mediante la adición de cápitas, etc. Hay sutiles variaciones en la interpretación. Hay sutiles variaciones en la interpretación. El angloparlante moderno se encuentra con una falta de material en inglés debido a la preferencia por el neolatín por parte de los eruditos ingleses. Gigantes intelectuales ingleses como Edmund Halley e Isaac Newton, descendientes propios de la tradición helenística de las matemáticas y la astronomía, sólo pueden ser leídos e interpretados traducidos por poblaciones de angloparlantes no familiarizados con las lenguas clásicas; es decir, la mayoría.
Las presentaciones escritas íntegramente en inglés nativo comienzan a finales del siglo XIX. Cabe destacar el Treatise on Conic Sections de Heath. Su extenso comentario preliminar incluye elementos tales como un léxico de términos geométricos apolíneos que dan el griego, los significados y el uso.[8] Comentando que "el volumen aparentemente portentoso del tratado ha disuadido a muchos de intentar conocerlo",[9] promete añadir encabezamientos, cambiando superficialmente la organización, y aclarar el texto con notación moderna. Así pues, su obra hace referencia a dos sistemas de organización, el suyo y el de Apolonio, a los que se dan concordancias entre paréntesis.
La obra de Heath es indispensable. Enseñó durante todo el principio del siglo XX, falleciendo en 1940, pero mientras tanto se desarrollaba otro punto de vista en el John's College (Annapolis/Santa Fe), que había sido una escuela militar desde la época colonial, precediendo a la United States Naval Academy en Annapolis, Maryland, a la que es adyacente, en 1936 perdió su acreditación y estaba al borde de la quiebra. Desesperado, el consejo llamó a Stringfellow Barr y Scott Buchanan de la Universidad de Chicago, donde habían estado desarrollando un nuevo programa teórico para la enseñanza de los clásicos. Aprovechando la oportunidad, en 1937 instituyeron el "nuevo programa" en St. John's, más tarde denominado programa de Grandes Libros, un plan de estudios fijo que enseñaría las obras de algunos contribuyentes clave a la cultura de la civilización occidental. En St. John's, Apolonio llegó a ser enseñado como él mismo, no como un adjunto a la geometría analítica.
El tutor de Apolonio fue R. Catesby Taliaferro, recién doctorado en 1937 por la Universidad de Virginia. Fue tutor hasta 1942 y después durante un año en 1948, proporcionando él mismo las traducciones al inglés, traduciendo el Almagesto de Ptolomeo y las Cónicas de Apolonio. Estas traducciones pasaron a formar parte de la serie Grandes libros del mundo occidental de la Encyclopædia Britannica. Sólo se incluyen los libros I-III, con un apéndice para temas especiales. A diferencia de Heath, Taliaferro no intentó reorganizar a Apolonio, ni siquiera superficialmente, ni reescribirlo. Su traducción al inglés moderno se ajusta bastante al griego. Utiliza en cierta medida la notación geométrica moderna.
Al mismo tiempo que la obra de Taliaferro, Ivor Thomas, un don de Oxford de la época de la Segunda Guerra Mundial, se interesaba intensamente por las matemáticas griegas. Planeó un compendio de selecciones, que vio la luz durante su servicio militar como oficial del Regimiento Real de Norfolk. Tras la guerra encontró un hogar en la Loeb Classical Library, donde ocupa dos volúmenes, todos traducidos por Thomas, con el griego a un lado de la página y el inglés al otro, como es habitual en la serie Loeb. La obra de Thomas ha servido de manual para la edad de oro de las matemáticas griegas. Para Apolonio sólo incluye principalmente las partes del Libro I que definen las secciones.
Heath, Taliaferro y Thomas satisficieron la demanda pública de Apolonio en traducción durante la mayor parte del siglo XX. El tema avanza. Traducciones y estudios más recientes incorporan nueva información y puntos de vista, además de examinar lo antiguo.
Libro I
El libro I presenta 58 proposiciones. Su contenido más destacado son todas las definiciones básicas relativas a los conos y las secciones cónicas. Estas definiciones no son exactamente iguales a las modernas de las mismas palabras. Etimológicamente las palabras modernas derivan de las antiguas, pero el etimónimo a menudo difiere en significado de su reflejo.
Una superficie cónica es generada por un segmento de recta girado alrededor de un punto de bisección tal que los puntos extremos trazan circunferencias, cada una en su propio plano. Un cono, una rama de la superficie cónica doble, es la superficie con el punto (ápice o vértice), el círculo (base), y el eje, una línea que une el vértice y el centro de la base.
Una "sección transversal" (latín sectio, griego tome) es un "corte" imaginario de un cono por un plano.
- Proposición I.3: "Si un cono es cortado por un plano que pasa por el vértice, la sección es un triángulo". En el caso de un cono doble, la sección son dos triángulos tales que los ángulos en el vértice son ángulos verticales.
- La proposición I.4 afirma que las secciones de un cono paralelas a la base son circunferencias con centro en el eje.[10]
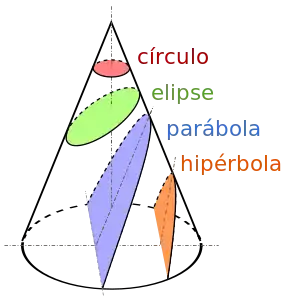
- La proposición I.13 define la elipse, que se concibe como el corte de un cono simple por un plano inclinado respecto al plano de la base y que interseca a ésta en una línea perpendicular al diámetro extendido de la base fuera del cono (no se muestra). El ángulo del plano inclinado debe ser mayor que cero, o la sección sería un círculo. Debe ser menor que el correspondiente ángulo de la base del triángulo axial, en el que la figura se convierte en una parábola.
- La proposición I.11 define una parábola. Su plano es paralelo a un lado de la superficie cónica del triángulo axial.
- La proposición I.12 define una hipérbola. Su plano es paralelo al eje. Corta a las dos cónicas del par, adquiriendo así dos ramas distintas (sólo se muestra una).
Los geómetras griegos estaban interesados en disponer figuras selectas de su inventario en diversas aplicaciones de la ingeniería y la arquitectura, como acostumbraban a hacer los grandes inventores, como Arquímedes. La demanda de secciones cónicas existía entonces y existe ahora. El desarrollo de la caracterización matemática había movido a la geometría en la dirección del álgebra geométrica griega, que presenta visualmente fundamentos algebraicos como la asignación de valores a segmentos de recta como variables. Utilizaban un sistema de coordenadas intermedio entre una cuadrícula de medidas y el sistema de coordenadas cartesianas. Las teorías de la proporción y la aplicación de áreas permitieron el desarrollo de ecuaciones visuales. (Véase más adelante Métodos de Apolonio).
Reconocimientos
- El cráter lunar Apollonius lleva este nombre en su memoria.[11]
Véase también
Referencias
- McElroy, Tucker (2005). A to Z of Mathematicians (en inglés). Nueva York: Facts on File. pp. 8-9. ISBN 0-8160-5338-3. Archivado desde el original el 18 de junio de 2022. Consultado el 24 de abril de 2022.
- Cecil Dampier, William. Historia de la ciencia y sus relaciones con la filosofía y la religión. Tecnos. p. 79. ISBN 84-309-0359-3.
- Biografías y Vidas. «Apolonio de Perga». Consultado el 15 de marzo de 2005.
- Boyer, Carl B. (julio de 1996). «Cap. IX: Apolonio de Perga». Historia de la matemática. Traducido por Mariano Martínez Pérez (5º edición). Alianza Editorial. pp. 189-208. ISBN 978-84-206-8094-1.
- Moreno Castillo, Ricardo (2005). Plücker y Poncelet. Dos modos de entender la geometría, pág. 22. Nivola libros y ediciones S. L. ISBN 84-95599-92-9.
- L. S. Pontriaguin Método de coordenadas URSS Moscú (2011) ISBN 978-5-396-00054-4
- Toomer, Gerald J. (1990). Apollonius: Conics Books V to VII : the Arabic Translation of the Lost Greek Original in the Version of the Banū Mūsā. New York, NY: Springer New York. pp. xvi-xviii. ISBN 1461389879.
- Apollonius of Perga y Heath, 1896, pp. clvii-clxx
- Apollonius of Perga y Heath, 1896, p. vii
- Nótese que los geómetras griegos no definían el círculo, la elipse y otras figuras como secciones cónicas. Esto sería una definición circular, ya que el cono se definió en términos de un círculo. Cada figura tiene su propia definición geométrica y, además, se está demostrando que es una sección cónica.
- «Apollonius». Gazetteer of Planetary Nomenclature (en inglés). Flagstaff: USGS Astrogeology Research Program. OCLC 44396779.