Asociaedro

En matemáticas, un asociaedro Kn es un politopo convexo (n-2)-dimensional en el que cada vértice corresponde a una forma de insertar correctamente la apertura y el cierre de un conjunto de paréntesis en una cadena de n letras, y las aristas corresponden a una aplicación única de la propiedad asociativa. De manera equivalente, los vértices de un asociaedro corresponden a las triangulaciones de un polígono regular con n + 1 aristas, y las aristas corresponden a cambios de arista en los que se elimina una única diagonal de una triangulación y se reemplaza por una diagonal diferente. Los asociaedros también se denominan politopos de Stasheff en honor al trabajo de Jim Stasheff, quien los redescubrió a principios de la década de 1960[1] con posterioridad a un trabajo anterior sobre el tema de Dov Tamari.[2]

Asociaedro K5 (parte delantera)
Asociaedro K5 (parte trasera)
K5 es el diagrama de Hasse del retículo de Tamari T4
Las 9 caras del asociaedro K5.
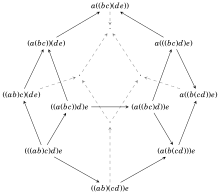
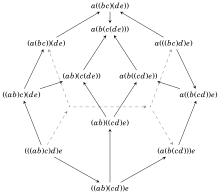
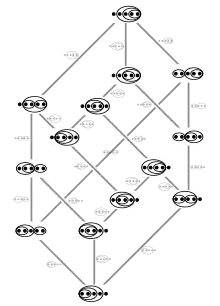
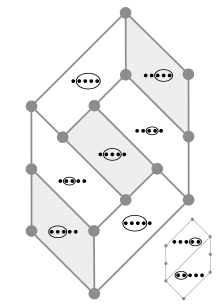
Cada vértice en el diagrama de Hasse anterior tiene los óvalos de las 3 caras adyacentes. Las caras cuyos óvalos se cruzan no se tocan

Ejemplos

El asociaedro unidimensional K3 representa los dos niveles de paréntesis ((xy)z) y (x(yz)) de tres símbolos, o las dos triangulaciones de un cuadrado. Es en sí mismo un segmento de línea recta.

El asociaedro bidimensional K4 representa los cinco niveles de paréntesis de cuatro símbolos, o las cinco triangulaciones de un pentágono regular. Es en sí mismo un pentágono y está relacionado con el diagrama pentagonal de una categoría monoidal.

El asociaedro tridimensional K5 es un eneaedro con nueve caras (tres cuadriláteros disjuntos y seis pentágonos) y catorce vértices, y su dual es el prisma triangular triaumentado.

Realización

Inicialmente Jim Stasheff consideró estos objetos como politopos curvilíneos. Posteriormente, se les dieron coordenadas como politopos convexos de varias maneras diferentes (véase la introducción sobre el tema de Ceballos, Santos y Ziegler (2015)).[3]

Un método para realizar un asociaedro es como un politopo secundario de un polígono regular.[3] En esta construcción, cada triangulación de un polígono regular con n + 1 lados corresponde a un punto en el espacio euclídeo (n + 1)-dimensional, cuya i-ésima coordenada es el área total de los triángulos incidentes en el i-ésimo vértice del polígono. Por ejemplo, las dos triangulaciones del cuadrado unidad dan lugar de esta manera a dos puntos de cuatro dimensiones con coordenadas (1, 1/2, 1, 1/2) y (1/2, 1 , 1/2, 1). La envolvente convexa de estos dos puntos es la realización del asociaedro K3. Aunque está definido en un espacio de 4 dimensiones, forma un segmento de recta (un politopo de dimensión 1) dentro de ese espacio. De manera similar, el asociaedro K4 se puede realizar de esta manera como un pentágono en un espacio euclídeo de cinco dimensiones, cuyas coordenadas de vértice son las permutaciones cíclicas del vector (1, 2 + f, 1 , 1 + f, 1 + f), donde f denota el número áureo. Debido a que los posibles triángulos dentro de un hexágono tienen áreas que son múltiplos enteros entre sí, esta construcción se puede utilizar para dar coordenadas enteras (en seis dimensiones) al asociaedro tridimensional K5. Sin embargo (como ya muestra el ejemplo de K4) esta construcción en general conduce a números irracionales como coordenadas.

Otra realización, debida a Jean-Louis Loday, se basa en la correspondencia de los vértices del asociaedro con un árbol binario de n hojas, y produce directamente coordenadas enteras en un espacio de (n − 2) dimensiones. La coordenada i de la realización de Loday es aibi, donde ai es el número de hojas descendientes del hijo izquierdo del nodo interno i del árbol (en orden de izquierda a derecha) y bi es el número de descendientes de hojas del hijo derecho.[4]

Es posible realizar el asociaedro directamente en el espacio (n − 2)-dimensional como un politopo para el cual todos los vectores normales a caras tienen coordenadas que son 0, +1 o −1. Hay exponencialmente muchas formas combinatoriamente distintas de hacer esto.[3][5]

Debido a que K5 es un poliedro con vértices en los que se juntan 3 aristas exclusivamente, es posible que exista un hidrocarburo (similar a los hidrocarburos platónicos) cuya estructura química está representada por el esqueleto de K5.[6] Este "asociaedrano" C14H14 tendría la notación SMILES: C12-C3-C4-C1-C5-C6-C2-C7-C3-C8-C4-C5-C6-C78. Sus aristas tendrían aproximadamente la misma longitud, pero los vértices de cada cara no serían necesariamente coplanares.

De hecho, K5 es un sólido casi coincidente de Johnson: parece que podría construirse a partir de cuadrados y pentágonos regulares, pero no lo es. O los vértices no serán del todo coplanares o las caras tendrán que distorsionarse ligeramente alejándose de la regularidad.

Número de caras k

 
   k= 1    2    3    4    5
n
1      1                               1
2      1    2                          3
3      1    5    5                    11
4      1    9   21   14               45
5      1   14   56   84   42         197

El número de caras (n − k)-dimensionales del asociaedro de orden n (Kn+1) viene dado por la posición (n,k) de la tabla triangular que se muestra a la derecha.[7]

El número de vértices en Kn+1 es el n-ésimo número de Catalan (diagonal derecha en el triángulo).

El número de facetas en Kn+1 (para n=2) es el n-ésimo número triangular menos uno (segunda columna del triángulo), porque cada faceta corresponde a un 2-subconjunto de los n objetos cuyas agrupaciones forman el retículo de Tamari Tn, excepto el 2-subconjunto que contiene el primer y el último elemento.

El número de caras de todas las dimensiones (incluido el asociaedro mismo como cara, pero sin incluir el conjunto vacío) es un número de Schröder-Hiparco (las sumas de las filas del triángulo).[8]

Diámetro
K5 como una bipirámide triangular de orden-4 truncada

A finales de la década de 1980, en relación con el problema de la distancia de rotación, Daniel Sleator, Robert Tarjan y William Thurston proporcionaron una prueba de que el diámetro del asociaedro n-dimensional Kn + 2 es como máximo 2n.  − 4 para una cantidad infinita de n y para todos los valores "suficientemente grandes" de n.[9] También demostraron que este límite superior es ajustado cuando n es lo suficientemente grande y conjeturaron que "suficientemente grande" significa "estrictamente mayor que 9". Esta conjetura fue demostrada en 2012 por Lionel Pournin.[10]

Amplitudes de dispersión
Véase también: Amplituedro

En 2017, Mizera[11] y Arkani-Hamed et al.[12] demostró que el asociaedro juega un papel central en la teoría de amplitudes de dispersión para la teoría del escalar cúbico bijunto. En particular, existe un asociaedro en el espacio de la cinemática de dispersión, y la amplitud de dispersión a nivel del árbol es el volumen del asociaedro dual.[12] El asociaedro también ayuda a explicar las relaciones entre las amplitudes de dispersión de cuerdas abiertas y cerradas en la teoría de cuerdas.[11]

Véase también
  • Cicloedro, un politopo cuya definición permite que los paréntesis se ajusten en orden cíclico.
  • Grafo de Flip, una generalización del 1-skeleton del asociaedro.
  • Permutoedro, un politopo que se define a partir de conmutatividad de forma similar a la definición del asociaedro a partir de la asociatividad.
  • Permutoasociaedro, un politopo cuyos vértices son permutaciones entre corchetes.
  • Retículo de Tamari, un retículo cuyo grafo es el esqueleto de un asociaedro.

Referencias
  1. Stasheff, James Dillon (1963), «Homotopy associativity of H-spaces. I, II», Transactions of the American Mathematical Society 108: 293-312, MR 0158400, doi:10.2307/1993609.. Revised from a 1961 Ph.D. thesis, Princeton University, MR 2613327.
  2. Tamari, Dov (1951), Monoïdes préordonnés et chaînes de Malcev, Thèse, Université de Paris, MR 0051833..
  3. Ceballos, Cesar; Santos, Francisco; Ziegler, Günter M. (2015), «Many non-equivalent realizations of the associahedron», Combinatorica 35 (5): 513-551, arXiv:1109.5544, doi:10.1007/s00493-014-2959-9..
  4. Loday, Jean-Louis (2004), «Realization of the Stasheff polytope», Archiv der Mathematik 83 (3): 267-278, MR 2108555, arXiv:math/0212126, doi:10.1007/s00013-004-1026-y..
  5. Hohlweg, Christophe; Lange, Carsten E. M. C. (2007), «Realizations of the associahedron and cyclohedron», Discrete & Computational Geometry 37 (4): 517-543, MR 2321739, arXiv:math.CO/0510614, doi:10.1007/s00454-007-1319-6..
  6. IPME document about mini-fullerenes - page 30 (page 9 in this PDF) shows in chapter “7. Fullerene of fourteen carbon atoms C14” under “b) Base-truncated triangular bipyramid (Fig. 16)” a K5 polyhedron
  7. (sucesión A033282 en OEIS)
  8. Holtkamp, Ralf (2006), «On Hopf algebra structures over free operads», Advances in Mathematics 207 (2): 544-565, MR 2271016, arXiv:math/0407074, doi:10.1016/j.aim.2005.12.004..
  9. Sleator, Daniel; Tarjan, Robert; Thurston, William (1988), «Rotation distance, triangulations, and hyperbolic geometry», Journal of the American Mathematical Society 1 (3): 647-681, MR 0928904, doi:10.1090/S0894-0347-1988-0928904-4..
  10. Pournin, Lionel (2014), «The diameter of associahedra», Advances in Mathematics 259: 13-42, MR 3197650, arXiv:1207.6296, doi:10.1016/j.aim.2014.02.035..
  11. Mizera, Sebastian (2017). «Combinatorics and topology of Kawai-Lewellen-Tye relations». Journal of High Energy Physics 2017: 97. arXiv:1706.08527. doi:10.1007/JHEP08(2017)097.
  12. Arkani-Hamed, Nima; Bai, Yuntao; He, Song; Yan, Gongwang (2018), «Scattering Forms and the Positive Geometry of Kinematics, Color and the Worldsheet», Journal of High Energy Physics 2018: 96, arXiv:1711.09102, doi:10.1007/JHEP05(2018)096..

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.