Autómata finito determinista
Un autómata finito determinista (abreviado AFD) es un autómata finito que además es un sistema determinista; es decir, para cada estado en que se encuentre el autómata, y con cualquier símbolo del alfabeto leído, existe siempre no más de una transición posible desde ese estado y con ese símbolo.
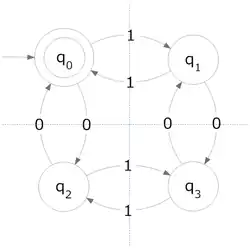
Autómata finito determinista que reconoce el lenguaje regular conformado exclusivamente por las cadenas con un número par de ceros y un número par de unos.
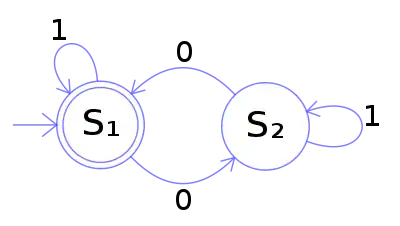
Ejemplo de AFD con dos estados. En nodo de la izquierda es inicial y de aceptación.
Definición formal
Formalmente, se define como una 5-tupla (Q, Σ, q0, δ, F) donde:[1]
- es un conjunto de estados;
- es un alfabeto;
- es el estado inicial;
- es una función de transición;
- es un conjunto de estados finales o de aceptación.
En un AFD no pueden darse ninguno de estos dos casos:
- Que existan dos transiciones del tipo δ(q,a)=q1 y δ(q,a)=q2, siendo q1 ≠ q2;
- Que existan transiciones del tipo δ(q, ε), donde ε es la cadena vacía, salvo que q sea un estado final, sin transiciones hacia otros estados.
Véase también
- Autómata finito
- Autómata finito no determinista
- Trie, un ejemplo de autómata finito determinista.
Referencias
- Chakraborty, Samarjit (17 de marzo de 2003). «Formal Languages and Automata Theory. Regular Expressions and Finite Automata». Computer Engineering and Networks Laboratory. Swiss Federal Institute of Technology (ETH) Zürich (en inglés): 17. Consultado el 30 de marzo de 2010.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.