Bitangentes de una cuártica
En geometría algebraica real, una curva cuártica general tiene 28 rectas bitangentes, rectas que son tangentes a la curva en dos lugares. Estas líneas existen en el plano proyectivo complejo, pero es posible definir curvas para las que todas estas 28 rectas bitangentes cuyas coordenadas son números reales, y por lo tanto pertenecen un espacio bidimensional.
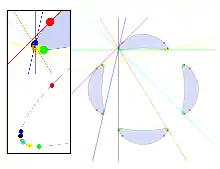

Una cuártica explícita con veintiocho bitangentes reales fue hallada por primera vez por (txt,)[1] Como Plücker demostró, el número de bitangentes reales de cualquier cuártica debe ser 28, 16, o un número inferior a 9. Otra cuártica con 28 bitangentes reales puede ser formada por el locus de los centros de elipses con longitudes de eje fijas, tangentes a dos líneas no paralelas.[2] Shioda (1995) dio una construcción diferente de una cuártica con veintiocho bitangentes, formado por la proyección de una superficie cúbica; veintisiete de las bitangentes de la curva de Shioda son reales, mientras que la vigésimo octava es la línea del infinito en el plano proyectivo.
Ejemplo
La curva de Trott, otra curva con 28 bitangentes reales, es el conjunto de puntos (x, y) que satisface la ecuación polinomial de cuarto grado:
Estos puntos forman una curva cuártica no singular, que tiene genus tres y que posee veintiocho bitangentes reales.[3]
Como los ejemplos de Plücker y de Blum y Guinand, la curva de Trott tiene cuatro óvalos separados, el número máximo para una curva de grado cuatro, y por lo tanto es una curva-M. Los cuatro óvalos pueden agruparse en seis pares diferentes de óvalos; para cada par de óvalos existen cuatro bitangentes que tocan ambos óvalos en el par: dos que los separan, y otras dos que no lo hacen. Además, cada óvalo limita una región no convexa del plano y tiene una bitangente que abarca la porción no convexa de su límite.
Conexiones con otras estructuras
La curva dual de una curva cuártica tiene 28 puntos dobles ordinarios reales, duales a las 28 bitangentes de la curva primaria.
Las 28 bitangentes de una cuártica también pueden colocarse en correspondencia con símbolos de la forma
Donde a, b, c, d, e y f son todos cero o uno y donde
- ad + be + cf = 1 (mod 2).[4]
Existen 64 opciones para a, b, c, d, e y f, pero solo 28 de estas opciones producen una suma impar. También se puede interpretar a, b y c como las coordenadas homogéneas de un punto del plano de Fano y d, e y f como las coordenadas de una línea en el mismo plano proyectivo finito; la condición de que la suma es impar, equivale a exigir que el punto y la línea no se toquen entre sí, y hay 28 pares diferentes formados por un punto y una línea que no se tocan.
Los puntos y líneas del plano de Fano disjuntos de un par de puntos no incidentales forman un triángulo, y las bitangentes de una cuártica han sido considerados en correspondencia con los 28 triángulos del plano de Fano.[5] El grafo de Levi del plano de Fano es el grafo de Heawood, en el que los triángulos del plano de Fano están representados por 6-ciclos. Los 28 6-ciclos del gráfico de Heawood a su vez corresponden a los 28 vértices del Grafo de Coxeter.[6]
Las 28 bitangentes de una cuártica también corresponden a pares de las 56 líneas de una superficie de del Pezzo de grado-2,[5] y a las 28 características theta impares.
Las 27 rectas de una cúbica y las 28 bitangentes en una cuártica, junto con los 120 planos tritangentes de una curva séxtica canónica de género 4, forman una "trinidad" en el sentido de Vladímir Arnold, específicamente una forma de correspondencia de McKay,[7][8][9] y pueden ser relacionadas con muchos otros objetos matemáticos, incluyendo E7 y E8, como se discute en trinidades.
Notas
- See e.g.Gray (1982).
- Blum y Guinand (1964).
- Trott (1997).
- Riemann (1876);Cayley (1879).
- Manivel (2006).
- Dejter, Italo J. (2011), «From the Coxeter graph to the Klein graph», Journal of Graph Theory, arXiv:1002.1960, doi:10.1002/jgt.20597..
- le Bruyn, Lieven (17 de junio de 2008), Arnold’s trinities, archivado desde el original el 11 de abril de 2011, consultado el 1 de marzo de 2011.
- Arnold 1997, p. 13 – Arnold, Vladimir, 1997, Toronto Lectures, Lecture 2: Symplectization, Complexification and Mathematical Trinities, June 1997 (last updated August, 1998). TeX, PostScript, PDF
- (McKay y Sebbar, 2007, p. 11)
Referencias
- Blum, R.; Guinand, A. P. (1964), «A quartic with 28 real bitangents», Canadian Mathematical Bulletin 7: 399-404, doi:10.4153/cmb-1964-038-6..
- Cayley, Arthur (1879), «On the bitangents of a quartic», Salmon's Higher Plane Curves, pp. 387-389.. En "Los documentos matemáticos reunidos de Arthur Cayley", Andrew Russell Forsyth, ed., The University Press, 1896, vol. 11, pp. 221 - 223.
- Gray, Jeremy (1982), «From the history of a simple group», The Mathematical Intelligencer 4 (2): 59-67, MR 0672918, doi:10.1007/BF03023483.. Reimpreso en Levy, Silvio, ed. (1999), The Eightfold Way, MSRI Publications 35, Cambridge University Press, pp. 115-131, ISBN 0-521-66066-1, MR 1722415..
- Manivel, L. (2006), «Configurations of lines and models of Lie algebras», Journal of Algebra 304 (1): 457-486, doi:10.1016/j.jalgebra.2006.04.029..
- Plücker, J. (1839), Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie, Berlin: Adolph Marcus..
- Riemann, G. F. B. (1876), «Zur Theorie der Abel'schen Funktionen für den Fall p = 3», Ges. Werke, Leipzig, pp. 456-472.. Como citado por Cayley.
- Shioda, Tetsuji (1995), «Weierstrass transformations and cubic surfaces», Commentarii Mathematici Universitatis Sancti Pauli 44 (1): 109-128, MR 1336422. (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última)..
- Trott, Michael (1997), «Applying GroebnerBasis to Three Problems in Geometry», Mathematica in Education and Research 6 (1): 15-28..