Circunferencia polar (geometría)
En geometría, la circunferencia polar de un triángulo tiene su centro en el ortocentro del triángulo y la longitud de su radio al cuadrado es:
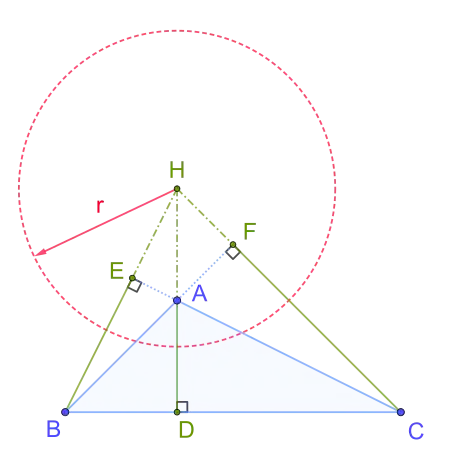
donde A, B, C designan los vértices y los ángulos correspondientes del triángulo, H es el ortocentro (la intersección de las alturas del triángulo), D, E y F son los pies de las alturas de los vértices A, B, y C respectivamente, R es el radio de la circunferencia circunscrita al triángulo y a, b y c son las longitudes de los lados opuestos a los vértices del triángulo A, B y C respectivamente.[1]: p. 176
Las primeras partes de la fórmula del radio reflejan el hecho de que el ortocentro divide las alturas en pares de segmentos cuyos productos de sus longitudes son iguales. La fórmula trigonométrica del radio muestra que la circunferencia polar solamente existe si el triángulo es obtuso, por lo que uno de sus ángulos debe ser obtuso y, por lo tanto, tiene un función trigonométrica negativa.
Propiedades
- Cualquier par de circunferencias polares de dos triángulos en un sistema ortocéntrico son ortogonales entre sí.[1]: p. 177
- Las circunferencias polares de los triángulos de un cuadrángulo completo forman un sistema coaxial.[1]: p. 179
- La circunferencia circunscrita de un triángulo, su circunferencia de los nueve puntos, su circunferencia polar y la circunferencia circunscrita de su triángulo tangencial son coaxiales.[2]: p. 241
- Existe una relación de inversión con respecto a la circunferencia polar entre los puntos E, A, F y los puntos B, D, C.
Véase también
Referencias
- Johnson, Roger A., Advanced Euclidean Geometry, Dover Publications, 2007 (orig. 1960).
- Altshiller-Court, Nathan, College Geometry, Dover Publications, 2007 (orig. 1952).
Enlaces externos
- Weisstein, Eric W. «Circunferencia polar». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. Consultado el 12 de junio de 2018.