Cadena de Pappus
En geometría, la cadena Pappus es un anillo de círculos entre dos círculos tangentes. Fue investigada por Pappus de Alejandría en el siglo III dC.
Construcción
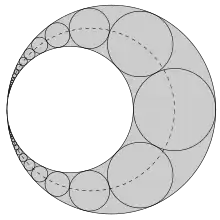
Un arbelos está definido por dos círculos, CU y CV, que son tangentes en el punto A y donde CU está contenido por CV. Denótense los radios de estos dos círculos como rU y rV, respectivamente, y que sus centros sean los puntos U y V. La cadena de Pappus consiste en los círculos en la región gris sombreada, que son tangentes externamente a CU (el círculo interno) y tangentes internamente a CV (el círculo externo). El radio, el diámetro y el centro del nésimo círculo de la cadena Pappus se denotan respectivamente como rn, dn y Pn.
Propiedades
Elipse
Todos los centros de los círculos en la cadena de Pappus están ubicados en una elipse común, por la siguiente razón. La suma de las distancias desde el nésimo círculo de la cadena de Pappus a los dos centros U y V de los círculos del arbelos, es igual a una constante
Así, los focos de esta elipse son U y V, los centros de los dos círculos que definen el arbelos; estos puntos corresponden a los puntos medios de los segmentos de línea AB y AC, respectivamente.
Coordenadas
Si r = AC/AB, entonces el centro del nésimo círculo de la cadena es:
Radios de los círculos
Si r = AC/AB, entonces el radio del nésimo círculo de la cadena es:
Inversión circular
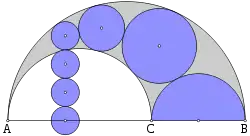
La altura h n del centro del nésimo círculo por encima del diámetro de la base ACB es igual a n veces dn.[1] Esto puede mostrarse realizando una inversión en un círculo centrado en el punto tangente A. La circunferencia de inversión se elige para cruzarse con el nésimo círculo perpendicularmente, de modo que se transforme en sí mismo. Los dos círculos del arbelos, CT y CV, se transforman en líneas paralelas tangentes a y que orlan al nésimo círculo; por lo tanto, los otros círculos de la cadena de Pappus se transforman en círculos del mismo diámetro. El círculo inicial C0 y el círculo final Cn contribuyen cada uno ½ dn a la altura hn, mientras que los círculos desde C1–Cn−1 contribuyen cada uno dn. Sumando estas contribuciones se obtiene la ecuación hn = n dn .
La misma inversión se puede utilizar para mostrar que los puntos donde los círculos de la cadena de Pappus son tangentes entre sí se encuentran en un círculo común. Como se señaló anteriormente, la inversión centrada en el punto A transforma los círculos del arbelos CU y CV en dos líneas paralelas, y los círculos de la cadena de Pappus en una pila de círculos de igual tamaño intercalados entre las dos líneas paralelas. Por lo tanto, los puntos de tangencia entre los círculos transformados se encuentran en una línea a medio camino entre las dos líneas paralelas. Al deshacer la inversión en el círculo, esta línea de puntos tangentes se transforma nuevamente en un círculo.
Cadena de Steiner
En estas propiedades de tener los centros en una elipse y las tangencias en un círculo, la cadena de Pappus es análoga a la cadena de Steiner, en la que varios círculos son tangentes a dos círculos.
Referencias
- Ogilvy, pp. 54–55.
Bibliografía
- Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 54–55. ISBN 0-486-26530-7.
- Bankoff, L. (1981). «How did Pappus do it?». En Klarner, D. A., ed. The Mathematical Gardner. Boston: Prindle, Weber, & Schmidt. pp. 112-118.
- Johnson, R. A. (1960). Advanced Euclidean Geometry: An elementary treatise on the geometry of the triangle and the circle (reprint of 1929 edition by Houghton Miflin edición). New York: Dover Publications. pp. 116–117. ISBN 978-0-486-46237-0.
- Wells, D. (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. pp. 5–6. ISBN 0-14-011813-6.
Enlaces externos
- Floer van Lamoen and Eric W. Weisstein. «Pappus Chain». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Tan, Stephen. «Arbelos».