Círculos tangentes
En geometría, los círculos tangentes (también conocidos como círculos osculadores) están situados sobre un plano común y se caracterizan por cortarse en un solo punto. Hay dos tipos de tangencia: interna (cuando uno de los círculos contiene al otro) y externa (en caso contrario).
Numerosas cuestiones y construcciones geométricas están relacionados con círculos tangentes; tales problemas a menudo tienen aplicaciones en la vida real, como la trilateración y la maximización del uso de materiales.
(NOTA: aunque la expresión circunferencia tangente es conceptualmente más correcta que círculo tangente, se ha preferido utilizar esta última por su mayor concisión)
Dos círculos dados
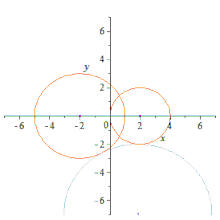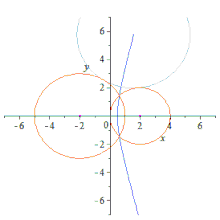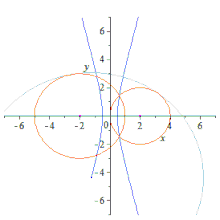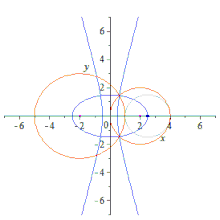
Dos círculos son mutua y externamente tangentes si la distancia entre sus centros es igual a la suma de sus radios.[1] Dos círculos son mutua e internamente tangentes si la distancia entre sus centros es igual a la diferencia de sus radios.
Cadenas de Steiner
Las cadenas de Steiner son conjuntos de círculos que son simultáneamente tangentes entre sí y a otros dos círculos que no se cortan entre ellos.
Cadenas de Pappus
La cadena de Pappus es un caso particular de la cadena de Steiner, en el que se parte de dos círculos tangentes exteriormente entre sí, y se continúa añadiendo círculos tangentes entre sí, al círculo envolvente de los dos círculos dados, y a uno de estos dos círculos.
Tres círculos dados: el problema de Apolonio
El problema de Apolonio es construir círculos que sean tangentes a tres círculos dados.
Tamiz de Apolonio
Si un círculo se inscribe iterativamente en los triángulos curvos intersticiales entre tres círculos mutuamente tangentes, resulta un tamiz de Apolonio, uno de los primeros fractales históricamente descritos.
Problema de Malfatti
El problema de Malfatti consiste en tallar tres cilindros de un bloque de mármol prismático de base triangular, utilizando la mayor cantidad de mármol posible. En 1803, Gian Francesco Malfatti conjeturó que la solución se obtendría al inscribir tres círculos mutuamente tangentes en el triángulo (un problema que anteriormente había sido considerado por el matemático japonés Ajima Naonobu). Estos círculos ahora se conocen como los círculos de Malfatti, aunque se ha demostrado que la conjetura es falsa.
Teorema de los seis círculos
El teorema de los seis círculos afirma que se puede dibujar una cadena de seis círculos de manera que cada círculo sea tangente a dos lados de un triángulo dado y también al círculo precedente en la cadena. La cadena se cierra; el sexto círculo siempre es tangente al primer círculo.
Generalizaciones
Los problemas que involucran círculos tangentes son a menudo generalizados a esferas. Por ejemplo, el problema de Fermat de encontrar esferas tangentes a cuatro esferas dadas es una generalización del Problema de Apolonio, mientras que el sexteto de Soddy es una generalización de una cadena de Steiner.
Véase también
- Rectas tangentes a círculos
- Teorema de empaquetamiento circular, el resultado de que cada gráfico plano puede realizarse mediante un sistema de círculos tangentes
- Hexafolio, figura formada por un anillo de seis círculos tangentes.
- El teorema de Feuerbach, sobre la tangencia de la circunferencia de los nueve puntos de un triángulo con su circunferencia inscrita y las exinscritas
- Teorema de los círculos de Descartes
- Círculo de Ford
- Círculo de Bankoff
- Círculos gemelos de Arquímedes
- Círculos arquimedianos
- Círculos de Schoch
- Círculos de Woo
- Arbelos
Referencias
| Control de autoridades |
|
|---|
Datos: Q7682871
Multimedia: Tangent circles / Q7682871