Círculo de quintas
En teoría musical, el ciclo o círculo de quintas (también conocido como círculo de cuartas) representa las relaciones entre los doce semitonos de la escala cromática, sus respectivas armaduras de clave y las tonalidades relativas (mayores y menores). Concretamente, se trata de una representación geométrica de las relaciones entre los 12 semitonos de la escala cromática en el espacio entre tonos. Dado que el término «quinta» define un intervalo o razón matemática que constituye el intervalo diferente de la octava más cercano y consonante, el círculo de quintas es una representación de los tonos o tonalidades disponiendo cerca los más estrechamente relacionados entre sí. Los músicos y los compositores usan el círculo de quintas para comprender y describir dichas relaciones. El diseño del círculo resulta útil a la hora de componer y armonizar melodías, construir acordes y desplazarse a diferentes tonalidades dentro de una composición.[1]
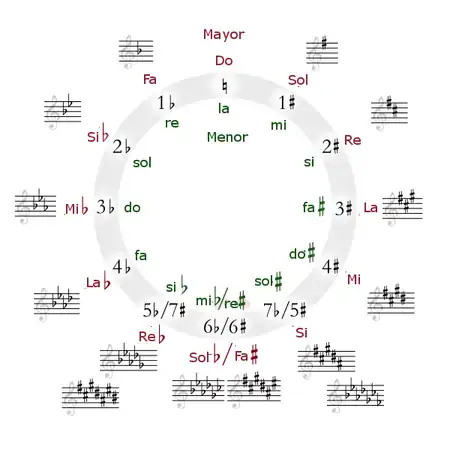

La tonalidad de Do mayor, que no tiene ni sostenidos ni bemoles, se sitúa convencionalmente en la parte alta del círculo (las 12 de un reloj). Siguiendo el círculo de quintas justas ascendentes a partir de Do mayor, la siguiente tonalidad, Sol mayor, tiene un sostenido; a continuación, Re mayor tiene 2 sostenidos, y así sucesivamente. De la misma manera, si se avanza en sentido contrario a las agujas del reloj desde el principio del círculo mediante intervalos de quintas descendentes o cuartas ascendentes, la primera tonalidad que encontramos, la tonalidad de Fa, tiene un bemol, la siguiente Si bemol tiene 2 bemoles, y así sucesivamente. Al final del círculo (las 6 del reloj), las tonalidades de sostenidos y de bemoles se superponen, con lo que aparecen pares de armaduras de tonalidades enarmónicas.
Empezando desde cualquier altura del ciclo y ascendiendo mediante intervalos de quintas temperadas iguales, se va pasando por todos los doce tonos en el sentido de las manecillas del reloj, para terminar regresando al tono inicial. Para recorrer los doce tonos en sentido contrario al reloj, es necesario ascender mediante cuartas, en lugar de quintas. La secuencia de cuartas da al oído una sensación de asentamiento o resolución (véase cadencia).
Estructura y uso
Los tonos de la escala cromática no solo están relacionados mediante el número de semitonos que los separa dentro de la escala, sino que también se relacionan armónicamente dentro del círculo de quintas. Invirtiendo la dirección del círculo de quintas, se crea el círculo de cuartas. Por norma general, el «círculo de quintas» se emplea en el análisis de música clásica, mientras que el «círculo de cuartas» se utiliza en el análisis de jazz, aunque esta distinción no es estricta. Dado que las quintas y las cuartas son intervalos que se componen, respectivamente, de 7 y 5 semitonos, la circunferencia de un círculo de quintas es un intervalo de nada menos que 7 octavas (84 semitonos), mientras que la circunferencia de un círculo de cuartas equivale a 5 octavas (60 semitonos).
Es interesante el círculo de quintas para facilitar las relaciones entre tonalidades, como por ejemplo, las tonalidades vecinas.
Armaduras de escalas diatónicas
El círculo de quintas se usa habitualmente para representar la relación entre escalas diatónicas. En este caso, las letras del círculo representan la escala mayor en la cual la nota en cuestión funciona como tónica. Los números situados en el interior del círculo representan cuántos sostenidos o bemoles tiene la armadura de la escala en cuestión. De esta forma, una escala mayor construida a partir de la nota La tiene 3 sostenidos en su armadura. La escala mayor que se construye a partir de la nota Fa tiene 1 bemol.
Para recorrer las escalas menores, se rotan 3 letras en sentido contrario al reloj, de manera que, por ejemplo, La menor no tiene ni sostenidos, ni bemoles y Mi menor tiene 1 sostenido. Más detalles se pueden ver en el tema de la tonalidad relativa.
Modulación y progresión armónica
Con frecuencia, la música tonal modula desplazándose entre escalas adyacentes dentro del círculo de quintas. Esto se debe a que las escalas diatónicas contienen 7 tonos diferentes contiguos en el círculo de quintas. En consecuencia, las escalas diatónicas que están separadas entre sí por una distancia de quinta justa comparten 6 de sus 7 notas. Además, las notas no comunes difieren solamente en un semitono. Por ello, la modulación mediante la quinta justa se puede realizar de forma extraordinariamente sencilla. Por ejemplo, para pasar de la secuencia fa – do – sol – re – la – mi – si de la escala de do mayor a la secuencia do – sol – re – la – mi – si – fa♯ de la escala de sol mayor, solo hay que cambiar el fa de la escala de do mayor a fa♯.
En la música tonal occidental, también se encuentran progresiones armónicas entre acordes cuyas notas fundamentales están relacionadas por una quinta justa. Por ejemplo, son habituales las progresiones de fundamentales como re - sol - do. Por este motivo, el círculo de quintas se puede emplear a menudo para representar la «distancia armónica» entre acordes.

Según los teóricos de la música, la función armónica (el uso, el papel y la relación de los acordes en la armonía), incluida la «sucesión funcional», se puede «explicar mediante el círculo de quintas (en el que, por tanto, el II grado de la escala está más cerca de la dominante que el IV grado)».[2] Según este planteamiento, la tónica se considera el final de la línea de movimiento que sigue una progresión armónica derivada del círculo de quintas.

Según Harmony in Western Music del director, educador y compositor estadounidense Richard Franko Goldman, «el acorde de IV se encuentra en realidad, en los mecanismos de relaciones diatónicas más sencillos, a la mayor distancia posible respecto al acorde de I. En relación al círculo [descendente] de quintas, aleja la progresión del acorde de I en lugar de acercarse a éste».[3] Por lo tanto, la progresión I-ii-V-I (una cadencia) daría una impresión de mayor conclusión o resolución que I-IV-I (una cadencia plagal). Goldman[4] coincide con el musicólogo canadiense Jean-Jacques Nattiez, quien sostiene que «el acorde de IV grado aparece mucho antes que el acorde de II y que el subsiguiente I final, en la progresión I-IV-viio-iii-vi-ii-V-I, y que también en esa posición se encuentra a más distancia de la tónica».[5]

Goldman sostiene que «históricamente, el uso del acorde de IV en el diseño armónico, y especialmente en cadencias, presenta algunas características curiosas. A grandes rasgos, se puede decir que el uso del acorde de IV en cadencias finales se hizo más habitual en el siglo XIX que en el XVIII, aunque también se puede considerar como un sustituto del acorde de ii cuando precede al de V grado. Como es lógico, también se puede interpretar como un acorde de ii7 incompleto (sin fundamental).»[3] La lenta aceptación de la secuencia IV-I en las cadencias finales queda explicada estéticamente por su falta de carácter conclusivo, motivada por la posición que ocupa en el círculo de quintas. El anterior uso de la secuencia IV-V-I se puede explicar mediante la creación de una relación entre IV y ii que permitiría que el IV grado sustituyera o funcionara como ii. Sin embargo, Nattiez califica este último argumento como «una solución pobre: tan solo la teoría de un acorde de ii sin fundamental puede permitir a Goldman afirmar que el círculo de quintas es completamente válido desde Bach hasta Wagner», o durante todo el período de la práctica común.[5]
Cierre del círculo en sistemas de afinación desiguales
Cuando un instrumento está afinado con el sistema del temperamento igual, la propia dimensión de las quintas conduce al «cierre» del círculo. Esto quiere decir que, si se ascienden 12 quintas partiendo de cualquier tono, se regresa a un tono del mismo tipo exactamente que el tono inicial, y a una distancia exacta de 7 octavas por encima de éste. Para obtener un cierre del círculo tan perfecto, la quinta se rebaja ligeramente respecto a su afinación justa (intervalo de razón 3:2).
Ascendiendo por quintas afinadas justas, no se llega a cerrar el círculo por una pequeña cantidad excedente, la coma pitagórica. En el sistema de afinación pitagórico, este problema se resuelve considerablemente acortando el intervalo de 1 de las 12 quintas, lo que la hace profundamente disonante. Esta quinta anómala se denomina quinta del lobo debido a que suena como el aullido de un lobo. El sistema de afinación mesotónico de 1/4 de coma emplea 11 quintas ligeramente menores que la quinta del temperamento igual y requiere una quinta del lobo más amplia y aún más disonante para cerrar el círculo. Otros sistemas de afinación más complejos que se basan en la afinación justa, como el temperamento de cinco límites, usan como máximo 8 quintas afinadas justas y como mínimo 3 quintas no justas (algunas son ligeramente menores y otras ligeramente mayores que la quinta justa) para cerrar el círculo.
En otras palabras
- Cómo tocar el círculo de quintas
 Quintas en 1 octava
Quintas en 1 octava Quintas en 1 octava
Quintas en 1 octava Quintas en 2 octavas - ascendente
Quintas en 2 octavas - ascendente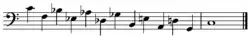 Quintas en 2 octavas - descendente
Quintas en 2 octavas - descendente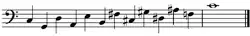 Cuartas en 2 octavas - ascendente
Cuartas en 2 octavas - ascendente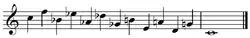 Cuartas en 2 octavas - descendente
Cuartas en 2 octavas - descendente Quintas en octavas múltiples - ascendente
Quintas en octavas múltiples - ascendente Quintas en múltiples octavas - descendente
Quintas en múltiples octavas - descendente Cuartas en múltiples octavas - ascendente
Cuartas en múltiples octavas - ascendente
Una manera fácil de visualizar el intervalo conocido como quinta consiste en mirar un teclado de un piano y, comenzando desde cualquier tecla, contar siete teclas hacia la derecha (tanto blancas como negras) para llegar hasta la siguiente nota del círculo mostrado anteriormente en esta página. 7 semitonos, la distancia entre la primera y la octava tecla de un piano, es una «quinta justa», denominada «justa» debido a que no es ni mayor ni menor, sino que es aplicable tanto a escalas y acordes mayores como menores, y «quinta» porque, a pesar de constituir una distancia de 7 semitonos en un teclado, constituye una distancia de 5 tonos en una escala mayor o menor.
Una manera sencilla de escuchar la relación entre estas notas es tocarlas en el teclado de un piano. Si se recorre el círculo de quintas en sentido inverso, dará la impresión de que las notas caen unas dentro de otras. Esta relación auditiva es la que describen las matemáticas.[cita requerida]
Las quintas justas pueden estar afinadas por el sistema justo o temperado. Dos notas cuyas frecuencias difieren en una relación de 3:2 forman el intervalo conocido como una quinta justa de afinación justa. Descendiendo de tal forma por las 12 quintas no se regresa al tono original tras haber recorrido todo el círculo, por lo que la relación 3:2 puede quedar ligeramente desafinada, o temperada. La afinación temperada hace posible que las quintas justas sigan un ciclo y que las obras musicales puedan transponerse, es decir, tocarse en cualquier tonalidad en un piano u otro instrumento de sonidos fijos sin distorsionar su armonía. El principal sistema de afinación empleado en los instrumentos occidentales (especialmente los de teclado y con trastes) en la actualidad se denomina temperamento igual de doce notas.
Historia
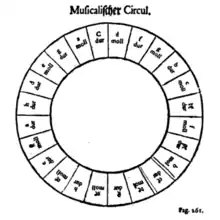
En 1679, el compositor y teórico ruso Nikolái Diletski escribió un tratado llamado Grammatika[6] sobre composición, siendo el primero de su naturaleza, dedicado a composiciones polifónicas de estilo occidental.[6] Este tratado enseñaba cómo escribir kontserty, polifonía a capela, que normalmente se basaban en textos litúrgicos y se creaban mediante la unión de secciones musicales contrastantes en ritmo, medidas, material melódico y agrupaciones de voces.[6] La intención de Diletski era que su tratado fuese una guía a la composición que se atuviese a las reglas de la teoría musical. Es en el tratado Grammatika donde apareció el primer círculo de quintas, que era empleado como recurso de aprendizaje por los estudiantes de composición. Mediante su círculo de quintas, Diletski demostró que se podía ampliar un conjunto de ideas musicales empleando otras letras parecidas.[6]
Conceptos relacionados
El círculo diatónico de quintas abarca únicamente miembros de la escala diatónica. De esta manera, contiene una quinta disminuida: por ejemplo, en do mayor se encuentra entre si y fa.
Por progresión por quintas se entiende generalmente un círculo que recorre los acordes diatónicos por quintas, incluidos un acorde disminuido y una progresión por quinta disminuida:

El círculo cromático
El círculo de quintas está estrechamente relacionado al círculo cromático, que también dispone los 12 tonos del temperamento igual en un orden circular. Una diferencia fundamental entre los dos círculos consiste en que el círculo cromático puede interpretarse como un espacio continuo en el que cada punto del círculo corresponde a un tono concebible y cada tono concebible corresponde, a su vez, a un punto del círculo. Por el contrario, el círculo de quintas es fundamentalmente una estructura discreta en la que no existe una forma evidente de asignar un tono a cada uno de sus puntos. En este sentido, los dos círculos son matemáticamente bastante distintos.
No obstante, los 12 tonos del temperamento igual pueden ser representados mediante el grupo cíclico de orden 12 o, igualmente, mediante las clases del residuo de módulo 12, . El grupo posee 4 generadores, que se pueden identificar como los semitonos ascendentes y descendentes y las quintas justas ascendentes y descendentes. El generador de semitonos da lugar a la escala cromática, mientras que la quinta justa da lugar al círculo de quintas.
Relación con la escala cromática
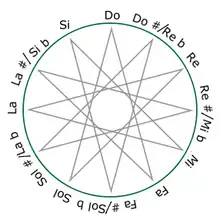
El círculo de quintas, o cuartas, puede trazarse a partir de la escala cromática mediante un proceso de multiplicación y viceversa. Para pasar del círculo de quintas a la escala cromática (en notación en números enteros), hay que multiplicar por 7 (M7), y para el círculo de cuartas es necesario multiplicar por 5 (P5).
A continuación, se incluye una demostración de este procedimiento. Se empieza con una tupla (secuencia de tonos) ordenada de 12 números enteros
- (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)
que representan las notas de la escala cromática: 0 = do, 2 = re, 4 = mi, 5 = fa, 7 = sol, 9 = la, 11 = si, 1 = do♯, 3 = re♯, 6 = fa♯, 8 = sol♯, 10 = la♯. Entonces, se multiplica toda la tupla de 12 por 7:
- (0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77)
y después se aplica una reducción del módulo 12 a cada uno de los números (se divide por 12 cada número, y el módulo, es el resto):
- (0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)
lo que equivale a
- (do, sol, re, la, mi, si, fa♯, do♯, sol♯, re♯, la♯, fa)
que es el círculo de quintas. Cabe recordar que esto es enarmónicamente equivalente a:
- (do, sol, re, la, mi, si, sol♭, re♭, la♭, mi♭, si♭, fa)
Enarmonía
Las tonalidades situadas en la parte inferior del círculo de quintas se escriben frecuentemente con bemoles y sostenidos, intercambiándose entre sí fácilmente mediante el uso de enarmónicos. Por ejemplo, la tonalidad de si mayor, con 5 sostenidos, es el equivalente enarmónico de la tonalidad de do♭ mayor, con 7 bemoles. Pero el círculo de quintas no se detiene en 7 sostenidos (do♯) o 7 bemoles (do♭). Siguiendo el mismo patrón, se puede construir un círculo de quintas con todas las tonalidades de sostenidos, o con todas las de bemoles.
Después de do♯ menor, viene la tonalidad de sol♯ menor (siguiendo el patrón de desplazarse a una quinta ascendente y, al mismo tiempo, equivalente enarmónico de la tonalidad de la♭ menor). El octavo sostenido se sitúa en el fa♯, con lo que se convierte en fa![]() (doble sostenido). La tonalidad de re♯ menor, con 9 sostenidos, tiene otro sostenido situado en el do♯, lo que lo convierte en do
(doble sostenido). La tonalidad de re♯ menor, con 9 sostenidos, tiene otro sostenido situado en el do♯, lo que lo convierte en do![]() . Las armaduras con bemoles funcionan de la misma manera: la tonalidad de mi mayor (4 sostenidos) es equivalente a la tonalidad de fa♭ mayor (una vez más, una quinta por debajo de la tonalidad de do♭ mayor, siguiendo el patrón de las armaduras con bemoles. El último bemol se sitúa en el si♭, convirtiéndolo en si
. Las armaduras con bemoles funcionan de la misma manera: la tonalidad de mi mayor (4 sostenidos) es equivalente a la tonalidad de fa♭ mayor (una vez más, una quinta por debajo de la tonalidad de do♭ mayor, siguiendo el patrón de las armaduras con bemoles. El último bemol se sitúa en el si♭, convirtiéndolo en si![]() ).
).
Véase también
Referencias
Notas
- «The Circle of Fifths: A Brief History» en www.Dummies.com, (consultado el 23 de febrero de 2009).
- Nattiez, 1990, página 225.
- Goldman, 1965, p. 68.
- Goldman, 1965, capítulo 3.
- Nattiez, 1990, p. 226.
- Jensen, 1992, página 305.
- McCartin, 1998, p. 364.
Bibliografía
- Específica
- D'Indy, Vincent: Cours de composition musicale, 1903. Citado en Nattiez, 1990.
- Goldman, Richard Franko: Harmony in Western Music. Nueva York: W. W. Norton, 1965.
- Jensen, Claudia R.: «A Theoretical Work of Late Seventeenth-Century Muscovy: Nikolai Diletskii's "Grammatika" and the Earliest Circle of Fifths» en Journal of the American Musicological Society, 45 (2):305–331, (verano 1992). (JSTOR)
- McCartin, Brian J.: «Prelude to Musical Geometry» en The College Mathematics Journal, 29 (5):354–370, nov. 1998. (abstract) (JSTOR)
- Nattiez, Jean-Jacques: Music and Discourse: Toward a Semiology of Music. Princeton University Press, 1990. (Google Libros)
- Adicional
- Lester, Joel: Between Modes and Keys: German Theory, 1592–1802. Pendragon Press, 1989.
- Miller, Michael: The Complete Idiot's Guide to Music Theory, 2ª ed. Indianapolis, IN: Alpha, 2005. ISBN 1-59257-437-8. (Google Libros)
- Purwins, Hendrik: «Profiles of Pitch Classes: Circularity of Relative Pitch and Key—Experiments, Models, Computational Music Analysis, and Perspectives». Tesis doctoral. Berlín: Technische Universität Berlín, 2005.
- Purwins, Hendrik; Blankertz, Benjamin & Obermayer, Klaus: «Toroidal Models in Tonal Theory and Pitch-Class Analysis» en Computing in Musicology, 15 ("Tonal Theory for the Digital Age"):73–98, 2007.
Enlaces externos
- Circle of Fifths Memory Technique Página de Oggen McGahan sobre teoría del círculo de quintas. (en inglés)
- circleoffifths.com Poster Teoría, gráficos y videos sobre teoría musical. (en inglés)
- Interactive Circle of Fifths Círculo de quintas interactivo. (en inglés)
- Decoding the Circle of Vths Sitio web que permite calcular las relaciones entre las diferentes tonalidades y los vectores que forman en el círculo de quintas. (en inglés)
- Bach's Tuning Página web de Bradley Lehman que habla sobre el sistema de afinación empleado por Johann Sebastian Bach y presenta una lista de abundantes recursos complementarios sobre el tema. (en inglés)
- Circle of Fifths – Diagram Gráfico del círculo de quintas. (en inglés)
- Circle of Fifths – In Bass Clef Esquema del círculo de quintas escrito en clave de fa. (en inglés)
- How to Improvise Around the Circle of Fifths Video que explica el círculo quintas y cómo usarlo en la improvisación (en inglés)
- Major Keys: How to use the Circle of Fifths Video que muestra cómo usar el círculo de quintas para las tonalidades mayores. (en inglés)
- Minor Keys: How to use the Circle of Fifths Video que muestra cómo usar el círculo de quintas para las tonalidades menores. (en inglés)
- A Circle of Fifths memory quiz Juego interactivo de preguntas sobre el círculo de quintas. (en inglés)
- La Utilidad del Ciclo de Quintas (I) Artículo que muestra cómo utilizar el círculo de quintas para las tonalidades mayores. (en español)
- La Utilidad del Ciclo de Quintas (II) Artículo que muestra cómo utilizar el círculo de quintas para deducir las alteraciones de los modos griegos. (en español)