Cobertura de vértices
En la disciplina matemática de la teoría de grafos, una cobertura de vértices (en inglés, vertex cover) o simplemente cobertura de un grafo, es un conjunto de vértices tales que cada arista del grafo es incidente a al menos un vértice del conjunto.
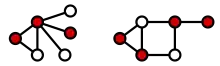

El problema de encontrar la menor cobertura de vértices en un grafo se denomina problema de la cobertura de vértices. En teoría de la complejidad computacional se ha demostrado que este es un problema NP-completo.
La cobertura de vértices y aristas está muy relacionada con los conjuntos independientes y apareamientos o matchings.
Definición
Una cobertura de vértices para un grafo G es un conjunto de vértices V en los que cada arco de G incide al menos en un nodo de V. La cobertura de vértices mínima es la más pequeña de las coberturas de vértices. El número de cobertura de vértices para un grafo G es el tamaño de la cobertura de vértices mínima.
Ejemplos
- Para cualquier grafo, el conjunto de todos sus vértices es trivialmente una cobertura de vértices.
- Un grafo bipartito completo tiene y .
Propiedades
- Para cualquier grafo : + máximo conjunto de vértices independientes = (Tibor Gallai 1959)
Referencias
- Gallai, Tibor "Über extreme Punkt- und Kantenmengen." Ann. Univ. Sci. Budapest, Eotvos Sect. Math. 2, 133-138, 1959.