Cuadratriz de Ozanam
La cuadratriz de Ozanam[1] es una curva plana estudiada por el matemático francés Jacques Ozanam (1640-1718), que presenta la particularidad de permitir cuadrar la superficie de un círculo, al llevar implícitamente el número pi en sus ordenadas. La fórmula que la define es la siguiente:[2]
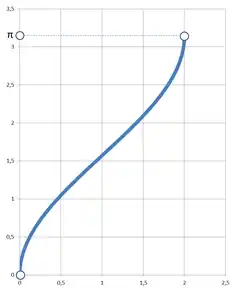 Cuadratriz de Ozanam |
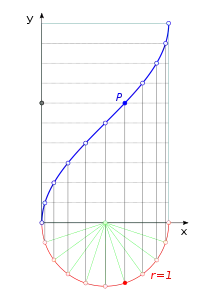 Construcción gráfica |
Dicha ecuación, dado que
- ,
también se puede escribir de la forma:
Esta segunda forma es la que permite deducir su construcción gráfica con mayor facilidad.
Construcción gráfica
Para el caso de , la ecuación de la curva queda reducida a
De acuerdo con la figura adjunta, cada punto P de la curva es el resultado de la intersección de dos rectas:
- Recta vertical: parte de un punto que pertenece al arco de circunferencia de color rojo
- Recta horizontal: pasa por un punto del eje y, cuya distancia al origen es igual a la longitud del arco de circunferencia comprendido entre el origen y el punto por el que pasa la recta vertical.
Su forma coincide con la de una helicoide inscrita en un cilindro circular recto, proyectada sobre un plano que contenga al eje del cilindro (véase cuadratriz).
Mecanismo para trazar la cuadratriz
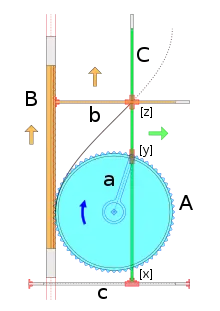
Un mecanismo capaz de dibujar una cuadratriz de Ozanam está formado por los componentes siguientes:[3]
- A >> una rueda dentada con una biela fija a, en cuyo extremo figura una deslizadera articulada [y]
- B >> una barra dentada engranada con la rueda, capaz de deslizarse verticalemente y con un brazo horizontal fijo b, insertado a su vez en la cruceta deslizadera [z]
- C >> un brazo vertical capaz de deslizarse horizontalmente según la deslizadera [x] a lo largo de la barra fija c. La barra C está insertada en la deslizadera articulada [y] y en la cruceta deslizadera [z]
Su funcionamiento comienza con el giro de la rueda dentada A, que impulsa hacia arriba la barra dentada B, y horizontalmente la barra lisa C (empujada por la biela a). La combinación de ambos movimientos se materializa en el centro de la cruceta [z], que describe el trazado de la cuadratriz de Ozanam.
Resulta obvio comprobar que cuando la rueda A ha girado 180° desde la posición horizontal de la biela a, la barra dentada B se ha desplazado verticalmente una distancia , coincidente con el semiperímetro de la la rueda A.
Véase también
Referencias
- Encyclopaedia of Mathematics: Orbit - Rayleigh Equation. Springer Science & Business Media. 2012. pp. 387 de 506. ISBN 9789401512374. Consultado el 20 de marzo de 2021.
- I. I. Artobolevskii (2013). Mechanisms for the Generation of Plane Curves. Elsevier. pp. 263 de 294. ISBN 9781483152424. Consultado el 19 de marzo de 2021.
- I. L ARTOBOLEVSKII (1964). «Mechanisms For The Generation Of Plane Curves». Internet Archive (en inglés). Consultado el 20 de marzo de 2021.