Cuadrilátero extangencial
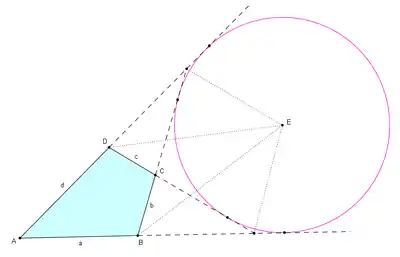
En geometría euclídea, un cuadrilátero extangencial es un cuadrilátero convexo donde las extensiones de los cuatro lados son tangentes a un círculo situado fuera del cuadrilátero.[1] También se le ha llamado cuadrilátero exescriptible.[2] El círculo se denomina su excircunferencia (o excírculo), su radio exradio y su centro el excentro (E en la figura). El excentro se encuentra en la intersección de las seis bisectrices internas de los ángulos correspondientes a cada par de vértices opuestos, a las bisectrices de los ángulos externos (bisectrices de los ángulos suplementarios) en los otros dos ángulos de vértice, y las bisectrices de ángulo externo en los ángulos formados donde las extensiones de lados opuestos se cruzan (véas la figura adjunta, donde cuatro de estas seis rectas son segmentos de línea punteada). El cuadrilátero extangencial está estrechamente relacionado con el cuadrilátero tangencial (donde los cuatro lados son tangentes a un círculo).
Otro nombre utilizado para designarlo es círculo escrito,[3] : p.69 pero esta denominación también se ha usado para un círculo tangente a un lado de un cuadrilátero convexo y las extensiones de los dos lados adyacentes. En ese contexto, todos los cuadriláteros convexos tienen cuatro círculos escritos, pero a lo sumo pueden tener un excírculo.[4]
Casos especiales
Los deltoides son ejemplos de cuadriláteros extangenciales. Los paralelogramos (que incluyen cuadrados, rombos y rectángulos ) pueden considerarse cuadriláteros extangenciales con exradio infinito, ya que satisfacen las caracterizaciones especificadas en la siguiente sección, pero el círculo no puede ser tangente a ambos pares de extensiones de lados opuestos (ya que son paralelas ).[4] Los cuadriláteros convexos cuyas longitudes laterales forman una progresión aritmética son siempre tangenciales, ya que satisfacen la caracterización dada a continuación relativa a las longitudes laterales adyacentes.
Características
Un cuadrilátero convexo es extangencial si y solo si posee seis bisectrices concurrentes. Estas son: las dos bisectrices internas de los ángulos formados por pares de vértices opuestos; las dos bisectrices de los ángulos externos en los otros dos ángulos de vértice; y las dos bisectrices de los ángulos externos formados donde se cruzan las extensiones de lados opuestos.[4]
Una característica más inmediata es que un cuadrilátero convexo con lados sucesivos a, b, c, d es extangencial si y solo si la suma de las longitudes de dos lados adyacentes es igual a la suma de los otros dos lados. Esto es posible de dos maneras diferentes, ya sea como
o
Esto fue demostrado por Jakob Steiner en 1846.[5] En el primer caso, el círculo está fuera del mayor de los vértices A o C, mientras que en el segundo caso está fuera del mayor de los vértices B o D, siempre que los lados del cuadrilátero ABCD son a = AB, b = BC, c = CD y d = DA. Una forma de combinar estas características con respecto a los lados, es que los valores absolutos de las diferencias entre los lados opuestos son iguales para los dos pares de lados opuestos[4]
Estas ecuaciones están estrechamente relacionadas con el teorema de Pitot para cuadriláteros tangenciales, donde las sumas de lados opuestos son iguales para los dos pares de lados opuestos.
Teorema de Urquhart
Si los lados opuestos de un cuadrilátero convexo ABCD se cruzan en E y F, entonces
La relación a la derecha lleva el nombre de L. M. Urquhart (1902-1966), aunque Augustus De Morgan la probó mucho antes, en 1841. Daniel Pedoe lo nombró el teorema más elemental en geometría euclídea, ya que solo se refiere a líneas rectas y distancias.[6] Mowaffac Hajja demostró que existe una equivalencia de facto, lo que hace que la igualdad del lado derecho sea otra condición necesaria y suficiente para que un cuadrilátero sea extangencial.
Comparación con un cuadrilátero tangencial
Algunas de las características métricas de los cuadriláteros tangenciales (la columna izquierda de la tabla) tienen contrapartidas muy similares para los cuadriláteros extangenciales (la columna central y derecha de la tabla), como se puede ver en la tabla que figura a continuación.[4] Por lo tanto, un cuadrilátero convexo posee un incírculo o un excírculo fuera de los propios vértices (dependiendo de la columna) si y solo si se cumple cualquiera de las cinco condiciones necesarias y suficientes dadas a continuación.
| Incírculo | Excírculo fuera de A o C | Excírculo fuera de B o D |
|---|---|---|
Las notaciones usadas en esta tabla son las siguientes: en un cuadrilátero convexo ABCD, las diagonales se intersecan en P. Los circunradios R1, R2, R3, R4 corresponden a los triángulos ABP, BCP, CDP, DAP; h1, h2, h3, h4 son las altituras desde P hacia los lados a = AB, b = BC, c = CD, d = DA respectivamente, en los mismos cuatro triángulos; e, f, g, h son las distancias desde los vértices A, B, C, D, respectivamente, hasta P; x, y, z, w son los ángulos ABD, ADB, BDC, DBC respectivamente; y Ra, Rb, Rc, Rd son los radios de los círculos externamente tangentes a los lados a, b, c, d respectivamente y las extensiones de los dos lados adyacentes para cada lado.
Área
Un cuadrilátero ABCD extangencial con lados a, b, c, d tiene área
Debe tenerse en cuenta que esta es la misma fórmula que la del área de un cuadrilátero circunscrito y también se deriva de la fórmula de Bretschneider de la misma manera.
Exradio
El exradio de un cuadrilátero extangencial con lados consecutivos a, b, c, d viene dado por[4]
donde K es el área del cuadrilátero. Para un cuadrilátero extangencial con lados dados, el exradio es máximo cuando el cuadrilátero también es cíclico (y, por lo tanto, un cuadrilátero exbicéntrico). Estas fórmulas explican por qué todos los paralelogramos tienen exradio infinito.
Cuadrilátero exbicéntrico
Si un cuadrilátero extangencial también posee un circuncírculo, se llama cuadrilátero exbicéntrico.[1] Entonces, dado que tiene dos ángulos suplementarios opuestos, su área está dada por
que es lo mismo que para un cuadrilátero bicéntrico.
Si x es la distancia entre el circuncentro y el excentro, entonces[1]
donde R y r son el circunradio y el exradio respectivamente. Esta es la misma ecuación que la del teorema de Fuss para un cuadrilátero bicéntrico. Pero al resolverla para x, se debe elegir la otra raíz de la ecuación cuadrática para el cuadrilátero exbicéntrico, en comparación con el bicéntrico. Por lo tanto, para el ex-bicéntrico se tiene que[1]
De esta fórmula se deduce que
lo que significa que el circuncírculo y el excírculo nunca pueden cruzarse entre sí.
Véase también
Referencias
- Radic, Mirko; Kaliman, Zoran and Kadum, Vladimir, "A condition that a tangential quadrilateral is also a chordal one", Mathematical Communications, 12 (2007) pp. 33–52.
- Bogomolny, Alexander, "Inscriptible and Exscriptible Quadrilaterals", Interactive Mathematics Miscellany and Puzzles, . Accessed 2011-08-18.
- K. S. Kedlaya, Geometry Unbound, 2006
- Josefsson, Martin, Similar Metric Characterizations of Tangential and Extangential Quadrilaterals, Forum Geometricorum Volume 12 (2012) pp. 63-77
- F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, p. 318.
- Hajja, Mowaffaq, A Very Short and Simple Proof of “The Most Elementary Theorem” of Euclidean Geometry, Forum Geometricorum Volume 6 (2006) pp. 167–169