Cuadrupletes arquimedianos
En geometría, los cuadrupletes arquimedianos son cuatro circunferencias congruentes asociadas con un arbelos. El término, introducido por Frank Power en el verano de 1998, designa a cuatro círculos resultantes de una construcción particular, cada uno de los cuales tiene el mismo área que uno de los dos círculos de Arquímedes, lo que los convierte en círculos arquimedianos.[1][2][3]
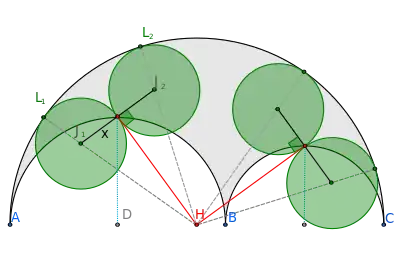
Construcción
Un arbelos se forma a partir de tres puntos colineales A, B y C y sus tres semicírculos con diámetros AB, AC y BC'. Los dos círculos más pequeños tienen radios r1 y r2, de lo que se deduce que el semicírculo más grande tiene radio r=r1+r2. Sean los puntos D y E el centro y el punto medio del arco, respectivamente, del semicírculo con el radio r1. Sea H sea el punto medio de la línea AC. Entonces, dos de los cuatro círculos del cuádruplete son tangentes a la línea HE en el punto E, y también son tangentes al semicírculo externo. Los otros dos círculos del cuadruplete se forman análogamente a partir del semicírculo con radio r2.
Prueba de congruencia
De acuerdo con la Proposición 5 de Arquímedes en el Libro de los Lemas, el radio común de los círculos gemelos de Arquímedes es:
Por el teorema de Pitágoras:
Luego, se trazan dos círculos con centros Ji; perpendiculares a HE; tangentes al semicírculo grande en el punto Li; tangentes al punto E y con radios iguales x. Usando el Teorema de Pitágoras:
También:
La combinación de estos da:
Mediante la expansión de la fórmula, y su factorización:
Resolviendo para x:
Esto demuestra que cada una de las áreas del cuadruplete arquímediano es igual a cada una de las áreas de los círculos gemelos de Arquímedes.[4]
Referencias
- Power, Frank (2005), «Some More Archimedean Circles in the Arbelos», en Yiu, Paul, ed., Forum Geometricorum 5 (publicado el 2 de noviembre de 2005), pp. 133-134, ISSN 1534-1178, consultado el 13 de abril de 2008.
- Online catalogue of Archimedean circles
- Clayton W. Dodge, Thomas Schoch, Peter Y. Woo, Paul Yiu (1999). "Those Ubiquitous Archimedean Circles". PDF.
- Bogomolny, Alexander. «Archimedes' Quadruplets». Archivado desde el original el 12 de mayo de 2008. Consultado el 13 de abril de 2008.
Lecturas relacionadas
- Arbelos: Book of Lemmas, Pappus Chain, Archimedean Circle, Archimedes' Quadruplets, Archimedes' Twin Circles, Bankoff Circle, S. ISBN 1156885493