Diagrama conmutativo
En matemática, y especialmente en teoría de categorías, un diagrama conmutativo es un diagrama de objetos (también conocidos como vértices) y morfismos (también conocidos como flechas o aristas) tales que todas las rutas directas en el diagrama con los mismos puntos finales y mismo comienzo conducen al mismo resultado por composición[1]. Los diagramas conmutativos desempeñan un papel fundamental en teoría de categorías al igual que las ecuaciones lo hacen en álgebra.
Nótese que un diagrama puede ser no conmutativo, por ejemplo la composición de diferentes rutas en el diagrama puede no dar el mismo resultado. Para clarificar, frases como «este diagrama conmutativo» o «el diagrama conmuta» pueden ser usadas.
Ejemplos
En el siguiente diagrama se expresa el primer teorema de isomorfía, conmutativamente significa que :
.svg.png.webp)
A continuación se muestra un cuadrado conmutativo genérico, en el cual
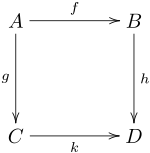
Símbolos
En los textos de álgebra, el tipo de morfismos puede ser denotado mediante el uso de diferentes flechas: monomorfismos con una [2], epimorfismos con una , e isomorfismos con una . La flecha a trazos típicamente representa la afirmación de que el morfismo indica que existe cada vez que el resto del esquema se cumple. Esto es bastante común que los textos a menudo no expliquen el significado de los diferentes tipos de flechas.
Verificación de conmutatividad
Conmutatividad da sentido a un polígono de cualquier número finito de caras (incluso únicamente 1 o 2), y un diagrama es conmutativo si cada subdiagrama poligonal es conmutativo.
Persecución de diagramas
La persecución o cacería de diagramas es un método de demostración matemática usado sobre todo en álgebra homológica. Dado un diagrama conmutativo, una demostración mediante persecución de diagramas implica el uso formal de las propiedades del diagrama, tales como los mapas injectivos o suprayectivos, o sucesiones exactas. Se construye un silogismo, para el cual se usa la representación gráfica del diagrama sólo como ayuda visual. De aquí se deduce que uno termina por "cazar" o "atrapar" elementos en torno al diagrama, hasta que el elemento o resultado deseado se verifica o se demuestra constructivamente.
Algunos ejemplos de demostración mediante cacería de diagramas son aquellas que usan el lema de los cinco, el lema de la serpiente, el lema zig-zag, y el lema de los nueve.
Diagramas como funtores
Un diagrama conmutativo en una categoría C puede ser interpretado como un functor de una categoría indexada J en C; uno llama a ese functor diagrama.
Más formalmente, un diagrama conmutativo es una visualización de un diagrama indexado por una categoría poset:
- Se dibuja un nodo para cada objeto en la categoría indexada,
- Una flecha para la generación del conjunto de morfismos,
- omitiendo la identidad de mapas y morfismos que puede ser expresados mediante composiciones,
- y la conmutatividad del diagrama (la igualdad de diferentes composiciones de mapas entre dos objetos) corresponde a la unicidad de un mapa entre dos objetos en una categoría poset.
Al contrario, dado un diagrama conmutativo, éste define una categoría poset:
- los objetos son los nodos,
- hay un morfismo entre dos objetos cualesquiera si y sólo si existe un camino (directo) entre los nodos,
- con la relación de que este morfismo es único (cualquier composición de mapas se define por su dominio y destino: este es el axioma de conmutatividad).
Sin embargo, no cada diagrama conmuta (la noción de diagrama estrictamente generaliza al diagrama conmutativo): más simplemente, el diagrama de un objeto simple con un endomorfismo (), o con dos flechas paralelas (; ), como el usado en la definición de ecualizador es necesario que no conmute. Además, los diagramas pueden ser un incómodos o imposibles de representar cuando el número de objetos y morfismos es grande (o incluso infinito).
Referencias
- Weisstein, Eric W. «Commutative Diagram». mathworld.wolfram.com (en inglés). Consultado el 25 de noviembre de 2019.
- «Maths - Category Theory - Arrow - Martin Baker». www.euclideanspace.com. Consultado el 25 de noviembre de 2019.
Bibliografía
- Adámek, Jiří; Horst Herrlich; George E. Strecker (1990), Abstract and Concrete Categories, John Wiley & Sons, ISBN 0-471-60922-6. Now available as free on-line edition (4.2MB PDF).
- Barr, Michael; Wells, Charles (2002), Toposes, Triples and Theories, ISBN 0-387-96115-1. Revised and corrected free online version of Grundlehren der mathematischen Wissenschaften (278) Springer-Verlag, 1983).
Véase también
Enlaces externos
- Weisstein, Eric W. «Diagram Chasing». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.