Diferencias en diferencias
Las diferencias en diferencias (a veces 'diferencia en diferencias",[1] 'DID',[2] o 'DD'[3]) es una técnica cuasi-experimental utilizada en econometría que mide el efecto de un tratamiento en un determinado período en el tiempo. A menudo se utiliza para medir el cambio inducido por un tratamiento o un evento en particular, aunque puede estar sujeto a ciertas tendencias (reversión a la media prejuicios, etc.) En contraste con una estimación dentro de los sujetos del efecto del tratamiento (que mide la diferencia en un resultado después y antes del tratamiento) o una estimación de entre-sujetos del efecto del tratamiento (que mide la diferencia en el resultado entre los grupos de tratamiento y control), el estimador DID representa la diferencia entre el pre-post tratamiento, dentro de los grupos de tratamiento y control.
Introducción
Diferencia en diferencias (DD)[4] es un método econométrico y de evaluación de impacto cuasiexperimental que consiste en medir el efecto que tiene una intervención sobre un grupo de tratamiento respecto a un grupo de comparación que no tiene la intervención a través del tiempo.
El método DD requiere datos panel o longitudinales, es decir, datos para las mismas unidades de análisis en diferentes puntos en el tiempo.[5]. DD permite establecer causalidad para conocer si un programa o una intervención causa o no una mejora en la población atendida, es decir, si los programas analizados funcionan o no.
El término “diferencia en diferencias” alude a que este método calcula el efecto de la intervención como una resta entre dos restas. La primera resta sería el resultado que se observa en el grupo de tratamiento después de recibir la intervención menos el resultado que se observó antes; y la segunda sería el resultado que se observa en el grupo de comparación después menos el resultado que se observó antes (sin haber recibido la intervención). De esta forma, para calcular la diferencia en diferencias, se sustrae la primera resta de la segunda resta. De esta manera, DD calcula qué tanto cambió en el tiempo el grupo de tratamiento respecto a qué tanto cambió en el tiempo el grupo de comparación.
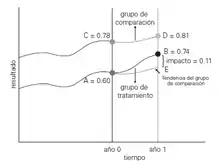
El siguiente gráfico ilustra el método de DD. La línea inferior ilustra la tendencia de los resultados del grupo de tratamiento, mientras que la línea superior la del grupo de comparación. La variable de interés (resultado) para el grupo de tratamiento va del punto A (año 0, antes del tratamiento) al punto B (año 1, después del tratamiento), mientras que la variable de interés del grupo de control va del punto C al D, respectivamente. (Fuente:Gertler et al. (2011, p. 97)).
La doble resta mencionada anteriormente corresponde a la diferencia de los resultados antes y después del programa en el grupo de tratamiento (B - A) y la diferencia de los resultados antes y después de la intervención en el grupo de comparación (D - C). Entonces, la DD se obtiene de la siguiente manera:
DD = (B – A) – (D – C) = (0.74 – 0.60) – (0.81 – 0.78) = 0.11
Según este cálculo, el efecto de la intervención sobre el grupo de tratamiento sería un aumento de 0.11 unidades en la variable de interés o resultado. Esto quiere decir que, entre el año 0 y el año 1, el grupo de tratamiento —que tenía la intervención— aumentó su variable de resultado en 0.11 unidades más de lo que la aumentó el grupo de comparación —que no tenía la intervención—.
Como otros métodos cuasiexperimentales, el método de DD depende de que se cumplan algunos supuestos clave para poder interpretar este cálculo como el efecto de la intervención de manera válida. El principal supuesto de DD es el de tendencias paralelas. Dicho supuesto estipula que la tendencia que se observa en la variable de interés o resultado para el grupo de comparación es igual a la tendencia que se habría observado en el grupo de tratamiento si no hubiera recibido la intervención. Es decir, que de no haber recibido el tratamiento, la variable de interés en el grupo de tratamiento cambiaría a la misma tasa de crecimiento que la variable de interés en el grupo de comparación.
Claramente, es imposible comprobar este supuesto dado que nunca se puede observar lo que le habría pasado al grupo de tratamiento si no hubiera recibido la intervención. No obstante, para verificar si es plausible que dicho supuesto se pudiera cumplir, generalmente los investigadores explorar las tendencias de ambos grupos en años anteriores al inicio del tratamiento. Si antes de dar el tratamiento las tendencias de ambos grupos eran idénticas (como se muestra en el gráfico), y sólo a partir de la introducción del tratamiento comienzan a diferir, es plausible suponer que en ausencia del tratamiento se habrían seguido comportando igual. También es recomendable explorar que no haya cambios concurrentes (o simultáneos) a la implementación del programa que hayan afectado la variable de interés de manera distinta en el grupo de tratamiento que en el grupo de control. Por ejemplo, si durante la implementación de la intervención sucede un choque exógeno que afecta sistemáticamente a uno de los dos grupos de manera distinta que al otro grupo, no se cumpliría el supuesto de tendencias paralelas y el cálculo de DD no sería válido.[4]
Definición formal
Considere el modelo:
donde es la variable dependiente por persona , teniendo en cuenta y . Las dimensiones de y puede ser por ejemplo del estado y el tiempo. y es entonces la intersección vertical para y respectivamente. es una variable dummy que indica el tratamiento de estado, es el efecto del tratamiento, y es un término de error.
Sea
,
,
,
,
,
y supongamos para simplificar, que and . Entonces
.
El supuesto de exogeneidad estricta implica entonces que:
.
Sin pérdida de generalidad, se supone que and , Dando el estimador DID
,
que se puede interpretar como el efecto del tratamiento indicado por .
Supuestos
Mantiene todos los supuestos del modelo de mínimos cuadrados ordinarios. Además, DID requiere un supuesto de tendencia paralela. La suposición de tendencia paralela nos dice que son los mismos en ambos y . Dado que la definición formal anterior representa fielmente la realidad, este supuesto se cumple automáticamente. Sin embargo, un modelo con bien puede ser más realista.
Como se ilustra a la derecha, el efecto del tratamiento es la diferencia entre el valor observado de y y lo que el valor de y habría sido con las tendencias paralelas, de no haber habido ningún tratamiento. El talón de Aquiles del DID es que cuando algo distinto del tratamiento en un grupo genera cambios en un grupo pero no en el otro, al mismo tiempo que el tratamiento, lo que implica una violación de la hipótesis tendencia paralela.
Para garantizar la precisión de la estimación de DID, se supone que la composición de los individuos de los dos grupos se mantenga sin cambios en el tiempo. Cuando se utiliza un modelo de DID, surgen diversas cuestiones que pueden poner en peligro los resultados, como la autocorrelación y Ashenfelter dips, ambos debe ser considerados y tratados.
Implementación
El método DID puede ser implementado de acuerdo a la siguiente tabla, donde la celda inferior derecha es el estimador DID.
| Diferencia | |||
|---|---|---|---|
| Cambio |
Ejecución de un análisis de regresión da el mismo resultado. Considere el modelo OLS
donde es una variable para , y es una variable dummy para . La variable compuesta es entonces una variable dummy que indica cuándo . Aunque no se muestra aquí con rigor, resulta que las estimaciones de este modelo son:
,
Aplicaciones
A continuación, se exponen dos ejemplos de estudios empíricos que han utilizado el método de diferencia en diferencias.
Ejemplo 1: Card y Krueger (1994)
El artículo de David Card y Krueger (1994)[6] busca aportar evidencia a la literatura económica sobre el efecto que puede tener el incremento en el salario mínimo en los niveles de empleo. La teoría convencional dice que “un aumento en el salario mínimo lleva a los empleadores perfectamente competitivos a recortar el empleo”,[7] ya que aumenta el monto salarial que tiene que pagar por empleado y, por lo tanto, disminuye la demanda por trabajadores. Sin embargo, hay estudios que demuestran lo contrario (Lawrence F. Katz y Krueger, 1992; Card, 1992a, Card, 1992b y Stephen Machin y Alan Manning, 1994 en Card y Krueger, 1994). Entonces, resultaba pertinente ofrecer otras pruebas alrededor de la relación entre salario mínimo y empleo.
Card y Krueger utilizan un experimento natural a partir de la promulgación de la Ley de Salarios Mínimos del estado de Nueva Jersey del 1 de abril de 1992. Dicha Ley promovió que el salario mínimo aumentara de 4.25 a 5.05 dólares la hora. Los autores toman este cambio de política pública como la introducción de una intervención o tratamiento, y comparan el nivel de empleo en el sector de comida rápida en Nueva Jersey (grupo de tratamiento) con las zonas contiguas en el Este de Pensilvania (grupo de control), en donde no aplicaba la Ley de Salarios Mínimos, tanto antes del cambio de la ley como después de la ley. Los autores entrevistaron a 473 restaurantes de comida rápida vía telefónica en ambos estados antes de la ley y a 410 después de la ley.
Card y Krueger señalan que Nueva Jersey es un estado pequeño con una economía vinculada a los estados aledaños. Por lo tanto, las tiendas de comida rápida en el Este de Pensilvania son un grupo de comparación natural para contrastar los cambios que pudo ocasionar el aumento en el salario mínimo en el nivel de empleo en Nueva Jersey. Además, los autores argumentan que la variación salarial en las tiendas de Nueva Jersey permite comparar las experiencias de las tiendas con salarios altos y bajos, y probar la validez de Pensilvania como grupo de comparación. Asimismo, los patrones estacionales de empleo son similares en ambos estados, así como entre las tiendas de salarios altos y bajos.
La Tabla 1 presenta los datos de Card y Krueger sobre el nivel de empleo en ambos estados, medido como el promedio de trabajadores de tiempo completo que laboraban en cada restaurante de comida rápida antes y después de la ley.
Tabla 1. Empleados promedio de tiempo completo en restaurantes de comida rápida
| Antes de la ley (feb. 1992) | Después de la ley (nov. 1992) | Diferencia | |
| Nueva Jersey (tratamiento) | 20.4 | 21.0 | 21.0 – 20.4 = 0.6 |
| Pensilvania (comparación) | 23.3 | 21.2 | 21.2 – 23.3 = –2.1 |
| Diferencia en diferencias = 0.6 – (–2.1) = 2.7 | |||
Fuente: elaboración propia con datos de Card y Krueger (1994).
La diferencia en diferencias es 2.7, lo cual indica que el número de empleados promedio en restaurantes de Nueva Jersey de febrero a noviembre de 1992 aumentó en 2.7 empleados más que lo que cambió el número de empleados promedio en restaurantes de Pensilvania durante el mismo período. En este sentido, la evidencia sugiere que el incremento en el salario mínimo en Nueva Jersey no redujo los niveles de empleo en esta industria, como supondría la teoría económica convencional. El aumento en el salario mínimo incluso parece haber incrementado el nivel de empleo de tiempo completo.
Como parte de los hallazgos de Card y Krueger, cabe mencionar que los precios de las comidas rápidas aumentaron en Nueva Jersey en relación con Pensilvania, lo que sugiere que gran parte de la carga del aumento en el salario mínimo se traspasó a los consumidores. Dentro de Nueva Jersey, sin embargo, los autores no encontraron evidencia de que los precios aumentaran más en las tiendas que se vieron más afectadas por el aumento del salario mínimo.
No obstante, es importante mencionar algunas debilidades del estudio de Card y Krueger que requieren que la interpretación de los resultados se tome con cautela. El estudio carece de validez externa, dado que los autores no tomaron en cuenta otras industrias u otros estados, por lo que la evidencia que presentan los autores no necesariamente es generalizable a otras poblaciones en otros contextos. Además, en este trabajo no se explora con suficiente profundidad la plausibilidad del supuesto de tendencias paralelas. Respecto a cambios concurrentes o simultáneos a la implementación de la nueva ley de salarios mínimos, Card y Krueger toman en cuenta que esto sucedió a la par de una recesión económica, pero argumentan que es poco probable que dicha situación afectara el impacto del salario mínimo.
Ejemplo 2: Duflo (2001)
La economista Esther Duflo (2001) explora la relación entre la inversión en infraestructura educativa y resultados como la escolaridad y el ingreso. Duflo utiliza un experimento natural de una política pública en Indonesia que, gracias a los ingresos petroleros extraordinarios, pudo invertir en la construcción de más de 61,000 escuelas primarias. La autora evalúa el efecto que tuvo esta construcción de escuelas sobre la escolaridad y los ingresos de los estudiantes beneficiados.[8]
Esta política de infraestructura educativa se implementó en Indonesia en 1973-1974 y 1978-1979. Se construyeron, en promedio, dos escuelas por cada 1,000 niños de 5 a 14 años en 1971. Esto representó un crecimiento de 100% en el número de escuelas en el país. El programa tuvo un costo de 500 millones de dólares (de 1990), que equivale a 1.5 por ciento del PIB en Indonesia en 1973. Las nuevas escuelas debían construirse en los distritos con las tasas de matriculación más bajas. Además, el gobierno contrató y capacitó a maestros, los cuales aumentaron en 43 por ciento.
Los datos que utilizó Duflo provienen de la encuesta intercensal en Indonesia de 1995. Obtuvo datos sobre los individuos que nacieron entre 1950 y 1972, su nivel educativo, su salario y el distrito en el que nacieron para identificar cuántas escuelas se construyeron ahí durante 1973-74 y 1978-79. La muestra se compone por 152,989 individuos, de los cuales 60,633 percibían un salario (el resto eran autoempleados). La edad del individuo y la concentración de escuelas construidas en su distrito son factores exógenos que se utilizan como variable instrumental en la ecuación de salarios. La misma estrategia se siguió para calcular el efecto de la calidad de la escuela en el retorno de educación y el efecto de la universidad en el ingreso.
En la Tabla 2, se presentan los datos con los que Duflo puso en práctica el método de DD para averiguar el efecto causal del programa. Primero, calculó las diferencias entre los distritos que tuvieron alta exposición a escuelas construidas por cada 1,000 niños y aquellos que tuvieron baja exposición. Posteriormente, calculó las diferencias entre niños de diferentes edades: los que tenían de 2 a 6 años y de 12 a 17 años en 1974 como el experimento de interés (Panel A), y los que tenían de 12 a 17 años y de 18 a 24 años en 1974 como un experimento de control (Panel B). Los cortes por edad representan mayor, menor o nula exposición al programa.
La autora señala que la diferencia en diferencias en este caso se interpreta como el efecto causal del programa de construcción de escuelas sobre los años de escolaridad y el ingreso, bajo el supuesto de que, en ausencia del programa, el aumento en el logro educativo no habría sido sistemáticamente diferente en las regiones más y menos expuestas al programa de infraestructura educativa (alta y baja).
Tabla 2. Promedio de los años de escolaridad y logaritmo natural de los salarios por nivel de exposición al programa y corte de edad
| Años de educación | Logaritmo del salario | |||||
| Nivel del programa en la región de nacimiento |
Nivel del programa en la región de nacimiento | |||||
| Alto | Bajo | Diferencia | Alto | Bajo | Diferencia | |
| Panel A: Grupo de tratamiento | ||||||
| De 2 a 6 años en 1974 | 8.49 | 9.76 | -1.27 | 6.61 | 6.73 | -0.12 |
| De 12 a 17 años en 1974 | 8.02 | 9.4 | -1.39 | 6.87 | 7.02 | -0.15 |
| Diferencia | 0.47 | 0.36 | 0.11 | -0.26 | -0.29 | 0.026 |
| Panel B: Grupo de control | ||||||
| De 12 a 17 años en 1974 | 8.02 | 9.4 | -1.39 | 6.87 | 7.02 | -0.15 |
| De 18 a 24 en 1974 | 7.7 | 9.12 | -1.42 | 6.92 | 7.08 | -0.16 |
| Diferencia | 0.32 | 0.28 | 0.034 | 0.05 | 0.063 | 0.007 |
Fuente: Fuente: elaboración propia con datos de Duflo (2001, p. 798).
Con estos datos, Duflo calcula la diferencia en diferencias dentro de cada panel para dos variables de interés o resultado: los años de escolaridad y el ingreso ganado (transformado en logaritmo natural). Duflo considera tanto la alta o baja exposición a la construcción de escuelas como los grupos de diferentes edades, como se mencionó antes. De esta manera puede estimar múltiples diferencias en diferencias con distintas combinaciones de estas categorías:
Para el Panel A:
- Años de escolaridad: (0.47) - (0.36) = 0.11
- Ingreso: (-0.26) - (-0.29) = 0.026
Para el Panel B:
- Años de escolaridad: (0.32) - (0.28) = 0.034
- Ingreso: (0.056) - (0.063) = 0.007
En este sentido, para el Panel A, un individuo que nació en una región de alta exposición al programa cuando era muy joven (2 a 6 años en 1974) obtiene, en promedio, 0.11 años más de escolaridad y el logaritmo de su ingreso en 1995 fue 0.026 más alto. Como el resultado del estimador de DD no es estadísticamente significativo, se puede interpretar que dos escuelas por cada 1,000 niños contribuyeron a un aumento en la escolaridad de 0.13 años (0.12 entre 0.90, que es la diferencia del número de escuelas construidas por cada 1,000 niños en las regiones de alta y baja exposición al programa) y un incremento salarial de 0.029 (0.026 entre 0.90) para niños de 2 a 6 años.
Para el Panel B, los resultados de los estimadores de DD son efectos menores, casi cercanos a cero (aunque estadísticamente significativos, por lo que Duflo desarrolla una estrategia econométrica en el resto del documento para obtener resultados más convincentes).
Duflo concluye que el aumento en la infraestructura educativa tiene un efecto positivo en los años de escolaridad y en el ingreso de las personas. Podría argumentarse, sin embargo, que el estudio tiene poca validez externa, por el contexto y la población tan particular en el que este programa se implementó en Indonesia.
Referencias
- Angrist y Pischke, 2008.
- Abadie, 2005.
- Bertrand, Duflo y Mullainathan, 2004.
- Gertler et al., 2011.
- Rabe-Hesketh y Skrondal, 2008.
- Card y Krueger, 1994.
- George J. Stigler, 1946 en Card y Krueger, 1994, p. 772.
- Duflo, 2001.
Bibliografía
- Angrist, J. D.; Pischke, J. S. (2008). Mostly harmless econometrics: An empiricist's companion. Princeton University Press. ISBN 9780691120348.
- Abadie, A. (2005). «Semiparametric difference-in-differences estimators». Review of Economic Studies 72 (1): 1-19. doi:10.1111/0034-6527.00321.
- Bertrand, M.; Duflo, E.; Mullainathan, S. (2004). «How Much Should We Trust Differences-in-Differences Estimates?». Quarterly Journal of Economics 119 (1): 249-275. doi:10.1162/003355304772839588.
- Card, David; Krueger, Alan B. (1994). «Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania». American Economic Review 84 (4): 772-793. JSTOR 2118030.
- Deaton, Angus; Cartwright, Nancy (2018). «Understanding and misunderstanding randomized controlled trials». Social Science & Medicine. Randomized Controlled Trials and Evidence-based Policy: A Multidisciplinary Dialogue (en inglés) 210: 2-21. ISSN 0277-9536. PMC 6019115. PMID 29331519. doi:10.1016/j.socscimed.2017.12.005. Consultado el 12 de octubre de 2021.
- Duflo, Esther (2001). «Schooling and Labor Market Consequences of School Construction in Indonesia: Evidence from an Unusual Policy Experiment». The American Economic Review 91 (4): 795-813. ISSN 0002-8282. Consultado el 12 de octubre de 2021.
- Gertler, P. J.; Martínez, S.; Premand, P.; Rawlings, L. B.; Vermeersch, C. M. (2011). La evaluación de impacto en la práctica. Banco Mundial. ISBN 978-0-8213-8681-1. doi:10.1596/978-0-8213-8541-8.
- Rabe-Hesketh, S.; Skrondal, A. (2008). Multilevel and longitudinal modeling using Stata. STATA press. ISBN 9781597180405.
Bibliografía adicional
- Bakija, Jon; Heim, Bradley (2008). How Does Charitable Giving Respond to Incentives and Income? Dynamic Panel Estimates Accounting for Predictable Changes in Taxation (14237). National Bureau of Economic Research. doi:10.3386/w14237.
- Conley, Timothy; Taber, Christopher (2005). Inference with “Difference in Differences” with a Small Number of Policy Changes (312). National Bureau of Economic Research. doi:10.3386/t0312.
- Khandker, S.; Koolwal, G. B.; Samad, H. (2009). Handbook on impact evaluation: quantitative methods and practices (en inglés). Banco Mundial.
Enlaces externos
- Difference in Difference Estimation, Healthcare Economist website