Distribución conjunta
En probabilidad, dados dos eventos aleatorios X y Y, la distribución conjunta de X e Y es la distribución de probabilidad de la intersección de eventos de X e Y, esto es, de los eventos X e Y ocurriendo de forma simultánea. En el caso de solo dos variables aleatorias se denomina una distribución bivariada, pero el concepto se generaliza a cualquier número de eventos o variables aleatorias.
| Tipo de distribución de probabilidad |
|---|
|
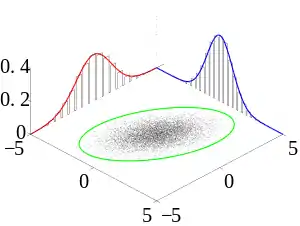
| Muchas observaciones de muestras (en negro) se observan a partir de una distribución de probabilidad conjunta. También se muestran las densidades marginales. |

Caso discreto
Para variables aleatorias discretas, la función de probabilidad conjunta está dada por la siguiente expresión:
Dadas esas probabilidades, se tiene que:
Caso continuo
Para las variables aleatorias continuas la función de densidad de probabilidad conjunta puede ser escrita como fX,Y(x, y) teniendo:
Donde fY|X(y|x) y fX|Y(x|y) dan la Probabilidad condicionada de Y dado X = x y de X dado Y = y respectivamente, y fX(x) y fY(y) dada la distribución marginal para X y Y respectivamente.
De nuevo, dado que son distribuciones de probabilidad:
Véase también
- Árbol Chow-Liu
- Copula (estadística)
- Redes Bayesianas
- Inferencia estadística