Distribución logarítmica

En teoría de la probabilidad, la distribución logarítmica es una distribución de probabilidad discreta derivada de la expansión en series de Maclaurin

${\displaystyle -\ln(1-p)=p+{\frac {p^{2}}{2}}+{\frac {p^{3}}{3}}+\cdots .}$

Distribución logarítmica
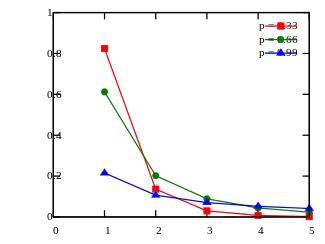La función estádefindia solo para valores enteros. Las líneas que conectan los puntos son solo guías para el ojo y no indican continuidad. Función de densidad de probabilidad
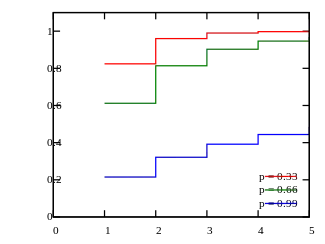El eje horizontal es el índice k. Función de distribución de probabilidad
Parámetros	${\displaystyle p\in (0,1)}$
Dominio	${\displaystyle k\in \{0,1,2,\ldots \}}$
Función de probabilidad (fp)	${\displaystyle {\frac {-1}{\ln(1-p)}}{\frac {p^{k}}{k}}}$
Función de distribución (cdf)	${\displaystyle 1+{\frac {\mathrm {B} (p;k+1,0)}{\ln(1-p)}}}$
Media	${\displaystyle {\frac {-1}{\ln(1-p)}}{\frac {p}{1-p}}}$
Moda	${\displaystyle 1}$
Varianza	${\displaystyle -{\frac {p^{2}+p\ln(1-p)}{(1-p)^{2}(\ln(1-p))^{2}}}}$
Función generadora de momentos (mgf)	${\displaystyle {\frac {\ln(1-pe^{t})}{\ln(1-p)}}{\text{ for }}t<-\ln p}$
Función característica	${\displaystyle {\frac {\ln(1-pe^{it})}{\ln(1-p)}}}$

A partir de ella, se obtiene

${\displaystyle \sum _{k=1}^{\infty }{\frac {-1}{\ln(1-p)}}\;{\frac {p^{k}}{k}}=1.}$

Por lo tanto, los valores

${\displaystyle f(k)={\frac {-1}{\ln(1-p)}}\;{\frac {p^{k}}{k}}}$

pueden interpretarse como los pesos de una distribución de probabilidad, que es, precisamente, la logarítmica (de parámetro p).

La función de probabilidad acumulada es

${\displaystyle F(k)=1+{\frac {\mathrm {B} (p;k+1,0)}{\ln(1-p)}}}$

donde B es la función beta incompleta.