Dodecagrama
Un dodecagrama es un polígono estrellado que tiene 12 vértices. Posee la configuración de una forma regular {12⁄5}, y comparte la misma disposición de vértices que un dodecágono regular, que puede considerarse como {12⁄1}.
| Dodecagrama | ||
|---|---|---|
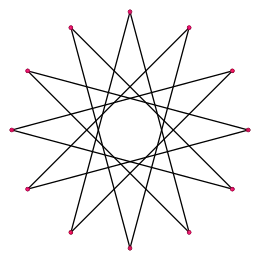 Dodecagrama | ||
| Características | ||
| Lados | 12 | |
| Vértices | 12 | |
| Símbolo de Schläfli |
{12⁄5} t{6/5} | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Ángulo interior | 30° | |
| Propiedades | ||
| Estrella, cíclica, equilátera, isógona, isotoxa | ||
El nombre "dodecagrama" combina el prefijo numérico dodeca- con el sufijo griego -gram. El sufijo -gram deriva de γραμμῆς (grammēs), que denomina una recta.[1]
Variantes isogonales
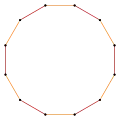
Un dodecagrama regular puede verse como un hexágono cuasitruncado, t{6⁄5}={12⁄5}. Se pueden construir otras variaciones isogonales con vértices igualmente espaciados con dos longitudes de aristas.
Dodecagramas como compuestos
Hay cuatro figuras estrelladas regulares dodecagrámicas: {12⁄2}=2{6}, {12⁄3}=3{4}, {12⁄4}=4{3} y {12⁄6}=6{2}. La primera es un compuesto de dos hexágonos, la segunda es un compuesto de tres cuadrados, la tercera es un compuesto de cuatro triángulos Los dos últimos pueden considerarse compuestos de dos hexagramas y el último como tres tetragramas.
 t{6} |
 |
 |
 t{6⁄5}={12⁄5} |
Superposicionando todos los dodecágonos y dodecagramas entre sí, incluido el compuesto degenerado de seis dígonos (segmentos de línea), {12⁄6}, produce el grafo completo K12 .
.svg.png.webp) 2{6} |
.svg.png.webp) 3{4} |
.svg.png.webp) 4{3} |
.svg.png.webp) 6{2} |
Grafo completo
Superponiendo todos los dodecágonos y dodecagramas entre sí, incluyendo la forma degenerada compuesta por seis segmentos, {12⁄6}, se obtiene el grafo completo K12:
 |
Negro: los doce puntos de esquina (nodos) Rojo: {12} dodecágono regular |
Dodecagramas regulares en poliedros
Los dodecagramas también se pueden incorporar en poliedros uniformes. A continuación se muestran los tres poliedros uniformes prismáticos que contienen dodecagramas regulares (no hay otros poliedros uniformes que contengan dodecagramas).
 Prisma dodecagrámico
Prisma dodecagrámico Antiprisma dodecagrámico
Antiprisma dodecagrámico Antiprisma cruzado dodecagrámico
Antiprisma cruzado dodecagrámico
Los dodecagramas también se pueden incorporar en las teselaciones con estrellas del plano euclídeo.
El simbolismo del dodecagrama
Se han utilizado dodecagramas o estrellas de doce puntas como símbolos relacionados con los temas siguientes:
- Las doce tribus de Israel, en el judaísmo
- Los doce discípulos, en el cristianismo
- Los doce olímpicos, en el politeísmo helénico
- Los doce signos del zodiaco
- La Orden Internacional de los Doce Caballeros e Hijas de Tabor, un grupo fraternal afroamericano
- La sociedad secreta ficticia Manus Sancti, en la serie Knights of Manus Sancti de Bryn Donovan
Véase también
- Estelación
- Polígono en forma de estrella
- Anexo:Lista de politopos regulares y compuestos
Referencias
- γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
Bibliografía
- Grünbaum, B. y GC Shephard; Tilings and Patterns, Nueva York: WH Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B.; Poliedros con caras huecas, Proceso de la Conferencia OTAN-ASI sobre Politopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43-70.
- John Horton Conway, Heidi Burgiel, Chaim Goodman-Strass, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 (Capítulo 26. pp. 404: Estrella-politopos regulares Dimensión 2)
Enlaces externos
- Esta obra contiene una traducción derivada de «Dodecagram» de Wikipedia en inglés, concretamente de esta versión del 2 de febrero de 2020, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.
- Weisstein, Eric W. «Dodecagram». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.