Ecuación de Camassa-Holm
En dinámica de fluidos, la ecuación de Camassa-Holm es la ecuación en derivadas parciales integrable, adimensional y no lineal.
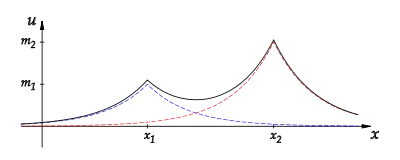
La evolución de las posiciones individuales peakon and , así como la evolución de las amplitudes peakon and Sin embargo, es menos trivial: esto se determina de una manera no lineal por la interacción
La ecuación fue introducida por Roberto Camassa y Darryl Holm[1] como un modelo bi- hamiltoniano para ondas en aguas poco profundas. En este contexto el parámetro κ es positivo y las soluciones de ondas solitarias son solitones suaves .
En el caso especial de que κ sea igual a cero, la ecuación de Camassa-Holm tiene soluciones de «pico de solitón»: solitones con un pico agudo, con una discontinuidad en el pico y la pendiente de declive de la onda.
Relación con las olas en aguas poco profundas
La ecuación de Camassa-Holm se puede escribir como el siguiente sistema de ecuaciones:[2]
siendo p la presión (adimensional) o elevación de la superficie. Esto muestra que la ecuación de Camassa-Holm es un modelo para ondas de aguas poco profundas con presión no hidrostática y una capa de agua en un lecho horizontal.
Las características de dispersión lineal de la ecuación de Camassa-Holm son:
| Símbolo | Nombre |
|---|---|
| Frecuencia angular | |
| Número de onda |
No es sorprendente que esto sea de una forma similar a la de la ecuación de Korteweg-de Vries, siempre que κ no sea cero. Para κ igual a cero, la ecuación de Camassa-Holm no tiene dispersión de frecuencia; además, la velocidad de fase lineal es cero para este caso. Como resultado, κ es la velocidad de fase para el límite de onda larga de k que se aproxima a cero, y la ecuación de Camassa-Holm es, si κ no es cero, un modelo para la propagación de onda unidireccional como la ecuación de Korteweg-de Vries .
Estructura de Hamilton
Introduciendo un impulso m tal como:
entonces existen dos soluciones hamiltonianas compatibles de la ecuación Camassa-Holm que son:
Integrabilidad
La ecuación Camassa-Holm es un sistema integrable. Integrabilidad significa que hay un cambio de variables (variables de ángulo de acción) de tal manera que la ecuación de evolución en las nuevas variables es equivalente a un flujo lineal a velocidad constante. Este cambio de variables se consigue estudiando un problema isospectral/de dispersión asociado, y recuerda el hecho de que los sistemas hamiltonianos clásicos integrables son equivalentes a los flujos lineales a velocidad constante en un toroide. La ecuación Camassa-Holm es integrable siempre que el momento
sea positivo —véase [3] y [4] para una descripción detallada del espectro asociado al problema isospectral—[3] para el problema espectral inverso en el caso de soluciones uniformes espacialmente periódicas, y [5] para el método de dispersión inversa en el caso de soluciones homogéneas que decaen al acercarse al infinito.
Soluciones exactas
Las ondas viajeras son soluciones que tienen la siguiente forma:
que representan ondas de forma permanente f que se propagan a velocidad constante c. Estas ondas se denominan ondas solitarias si son perturbaciones localizadas, es decir, si el perfil de onda f decae hacia el infinito. Si las ondas solitarias mantienen su forma y velocidad después de interactuar con otras ondas del mismo tipo, estas ondas solitarias se las denomina «solitones». Existe una estrecha relación entre la integrabilidad y los solitones.[6] En el caso límite en el que κ = 0 los solitones se convierten en picos; en forma de gráfico de la función f(x) = e−|x|, y se denominan picos. Esto se debe en parte al hecho de que, a diferencia de los peakons, los solitones lisos son relativamente fáciles de describir cualitativamente -son suaves, decaen exponencialmente rápido en el infinito, son simétricos con respecto a la cresta y tienen dos puntos de inflexión[7] - pero no se dispone de fórmulas explícitas. Observe también que las ondas solitarias son orbitalmente estables, es decir, que su forma es estable bajo pequeñas perturbaciones, tanto para los solitones suaves[7] como para los picos o apogeos.[8]
Olas rompientes
Los modelos de la ecuación Camassa-Holm rompen las olas: un perfil inicial suave con suficiente decaimiento en el infinito se convierte en una ola que existe para todos los tiempos o en una ola rompiente[9] que se caracteriza por el hecho de que la solución permanece limitada pero su pendiente se vuelve ilimitada en tiempo finito. El hecho de que las ecuaciones admitan soluciones de este tipo fue descubierto por Camassa y Holm[1] y estas consideraciones fueron puestas posteriormente sobre una base matemática firme.[10] Se sabe que la única forma en que las singularidades pueden ocurrir en las soluciones es en la forma de olas rompientes.[11] Además, a partir del conocimiento de un perfil inicial suave es posible predecir (a través de una condición necesaria y suficiente) si ocurre o no el rompimiento de una ola.[12] En cuanto a la continuación de las soluciones después del rompimiento de la ola, son posibles dos escenarios: el caso conservador[13] y el caso disipativo[14] (con el primero caracterizado por la conservación de la energía, mientras que el escenario disipativo da cuenta de la pérdida de energía debida a la rotura).
Soluciones asintóticas de larga duración
Puede demostrarse que para condiciones iniciales suaves de decaimiento suficientemente rápido con impulso positivo se divide en un número finito y solitones más una parte dispersiva de decaimiento. Más precisamente, se puede mostrar lo siguiente para .[15] Abreviación de . En la región de solitón las soluciones se dividen en solitones de combinación lineal finita. En la región la solución es asintóticamente dada por una función sinusoidal modulada cuya amplitud decae como . En la región la solución es asintóticamente dada por una suma de dos funciones sinusoidales moduladas como en el caso anterior. En la región la solución se descompone rápidamente. En el caso de que el estilo de la pantalla sea la solución se divide en una combinación lineal infinita de picos,[16] como se conjeturó anteriormente.[17]
Véase también
Referencias
- Camassa y Holm, 1993
- Loubet, 2005
- Constantin y McKean, 1999
- Constantin, 2001
- Constantin, Gerdjikov y Ivanov, 2006
- Drazin, P. G.; Johnson, R. S. (1989), Solitons: an introduction, Cambridge University Press, Cambridge.
- Constantin y Strauss, 2002
- Constantin y Strauss, 2000
- Whitham, G. B. (1974), Linear and nonlinear waves, Wiley Interscience, New York–London–Sydney.
- Constantin y Escher, 1998b
- Constantin, 2000,Constantin y Escher, 2000
- McKean, 2004
- Bressan y Constantin, 2007a
- Bressan y Constantin, 2007b
- Boutet de Monvel et al., 2009
- Eckhardt y Teschl, 2013
- McKean, 2003a
Bibliografía
- Beals, Richard; Sattinger, David H.; Szmigielski, Jacek (1999), «Multi-peakons and a theorem of Stieltjes», Inverse Problems 15 (1): L1-L4, Bibcode:1999InvPr..15L...1B, arXiv:solv-int/9903011, doi:10.1088/0266-5611/15/1/001.
- Boldea, Costin-Radu (1995), «A generalization for peakon's solitary wave and Camassa–Holm equation», General Mathematics 5 (1–4): 33-42.
- Boutet de Monvel, Anne; Kostenko, Aleksey; Shepelsky, Dmitry; Teschl, Gerald (2009), «Long-Time Asymptotics for the Camassa–Holm Equation», SIAM J. Math. Anal. 41 (4): 1559-1588, arXiv:0902.0391, doi:10.1137/090748500.
- Bressan, Alberto; Constantin, Adrian (2007a), «Global conservative solutions of the Camassa–Holm equation», Arch. Ration. Mech. Anal. 183 (2): 215-239, Bibcode:2007ArRMA.183..215B, doi:10.1007/s00205-006-0010-z.
- Bressan, Alberto; Constantin, Adrian (2007b), «Global dissipative solutions of the Camassa–Holm equation», Anal. Appl. 5: 1-27, doi:10.1142/S0219530507000857.
- Camassa, Roberto; Holm, Darryl D. (1993), «An integrable shallow water equation with peaked solitons», Phys. Rev. Lett. 71 (11): 1661-1664, Bibcode:1993PhRvL..71.1661C, PMID 10054466, arXiv:patt-sol/9305002, doi:10.1103/PhysRevLett.71.1661.
- Constantin, Adrian (2000), «Existence of permanent and breaking waves for a shallow water equation: a geometric approach», Annales de l'Institut Fourier 50 (2): 321-362, doi:10.5802/aif.1757.
- Constantin, Adrian (2001), «On the scattering problem for the Camassa–Holm equation», R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 457 (2008): 953-970, Bibcode:2001RSPSA.457..953C, doi:10.1098/rspa.2000.0701.
- Constantin, Adrian; Escher, Joachim (1998b), «Wave breaking for nonlinear nonlocal shallow water equations», Acta Math. 181 (2): 229-243, doi:10.1007/BF02392586.
- Constantin, Adrian; Escher, Joachim (2000), «On the blow-up rate and the blow-up set of breaking waves for a shallow water equation», Math. Z. 233 (1): 75-91, doi:10.1007/PL00004793.
- Constantin, Adrian; McKean, Henry P. (1999), «A shallow water equation on the circle», Commun. Pure Appl. Math. 52 (8): 949-982, doi:10.1002/(SICI)1097-0312(199908)52:8<949::AID-CPA3>3.0.CO;2-D.
- Constantin, Adrian; Strauss, Walter A. (2000), «Stability of peakons», Comm. Pure Appl. Math. 53 (5): 603-610, doi:10.1002/(SICI)1097-0312(200005)53:5<603::AID-CPA3>3.0.CO;2-L.
- Constantin, Adrian; Strauss, Walter A. (2002), «Stability of the Camassa–Holm solitons», J. Nonlinear Sci. 12 (4): 415-422, Bibcode:2002JNS....12..415C, doi:10.1007/s00332-002-0517-x.
- Constantin, Adrian; Gerdjikov, Vladimir S.; Ivanov, Rossen I. (2006), «Inverse scattering transform for the Camassa–Holm equation», Inverse Problems 22 (6): 2197-2207, Bibcode:2006InvPr..22.2197C, arXiv:nlin/0603019, doi:10.1088/0266-5611/22/6/017.
- Eckhardt, Jonathan; Teschl, Gerald (2013), «On the isospectral problem of the dispersionless Camassa-Holm equation», Adv. Math. 235 (1): 469-495, arXiv:1205.5831, doi:10.1016/j.aim.2012.12.006.
- Loubet, Enrique (2005), «About the explicit characterization of Hamiltonians of the Camassa–Holm hierarchy», J. Nonlinear Math. Phys. 12 (1): 135-143, Bibcode:2005JNMP...12..135L, doi:10.2991/jnmp.2005.12.1.11.
- McKean, Henry P. (2003a), «Fredholm determinants and the Camassa–Holm hierarchy», Comm. Pure Appl. Math. 56 (5): 638-680, doi:10.1002/cpa.10069.
- McKean, Henry P. (2004), «Breakdown of the Camassa–Holm equation», Comm. Pure Appl. Math. 57 (3): 416-418, doi:10.1002/cpa.20003.
- Parker, Allen (2005b), «On the Camassa–Holm equation and a direct method of solution. III. N-soliton solutions», Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 461 (2064): 3893-3911, Bibcode:2005RSPSA.461.3893P, doi:10.1098/rspa.2005.1537.
- Liao, S.J. (2013), «Do peaked solitary water waves indeed exist?», Communications in Nonlinear Science and Numerical Simulation 19 (6): 1792-1821, Bibcode:2014CNSNS..19.1792L, arXiv:1204.3354, doi:10.1016/j.cnsns.2013.09.042.
Bibliografía adicional
- Soluciones pico
- Beals, Richard; Sattinger, David H.; Szmigielski, Jacek (2000), «Multipeakons and the classical moment problem», Adv. Math. 154 (2): 229-257, arXiv:solv-int/9906001, doi:10.1006/aima.1999.1883.
- Teoría de la ola de agua
- Constantin, Adrian; Lannes, David (2007), «The hydrodynamical relevance of the Camassa–Holm and Degasperis–Procesi equations», Archive for Rational Mechanics and Analysis 192 (1): 165-186, Bibcode:2009ArRMA.192..165C, arXiv:0709.0905, doi:10.1007/s00205-008-0128-2.
- Johnson, Robin S. (2003b), «The classical problem of water waves: a reservoir of integrable and nearly-integrable equations», J. Nonlinear Math. Phys. 10 (suppl. 1): 72-92, Bibcode:2003JNMP...10S..72J, doi:10.2991/jnmp.2003.10.s1.6.
- Existencia, singularidad, bienestar, estabilidad, velocidad de propagación, etc.
- Bressan, Alberto; Constantin, Adrian (2007a), «Global conservative solutions of the Camassa–Holm equation», Arch. Ration. Mech. Anal. 183 (2): 215-239, Bibcode:2007ArRMA.183..215B, doi:10.1007/s00205-006-0010-z.
- Constantin, Adrian; Strauss, Walter A. (2000), «Stability of peakons», Comm. Pure Appl. Math. 53 (5): 603-610, doi:10.1002/(SICI)1097-0312(200005)53:5<603::AID-CPA3>3.0.CO;2-L.
- Holden, Helge; Raynaud, Xavier (2007a), «Global conservative multipeakon solutions of the Camassa–Holm equation», J. Hyperbolic Differ. Equ. 4 (1): 39-64, doi:10.1142/S0219891607001045.
- McKean, Henry P. (2004), «Breakdown of the Camassa–Holm equation», Comm. Pure Appl. Math. 57 (3): 416-418, doi:10.1002/cpa.20003.
- Olas viajeras
- Lenells, Jonatan (2005c), «Traveling wave solutions of the Camassa–Holm equation», J. Differential Equations 217 (2): 393-430, Bibcode:2005JDE...217..393L, doi:10.1016/j.jde.2004.09.007.
- Estructura de integrabilidad (simetrías, jerarquía de ecuaciones de solitones, leyes de conservación) y formulación geométrica diferencial.
- Fuchssteiner, Benno (1996), «Some tricks from the symmetry-toolbox for nonlinear equations: generalizations of the Camassa–Holm equation», Physica D 95 (3–4): 229-243, Bibcode:1996PhyD...95..229F, doi:10.1016/0167-2789(96)00048-6.
- Reyes, Enrique G. (2002), «Geometric integrability of the Camassa–Holm equation», Lett. Math. Phys. 59 (2): 117-131, doi:10.1023/A:1014933316169.
- Lenells, Jonatan (2005a), «Conservation laws of the Camassa–Holm equation», J. Phys. A 38 (4): 869-880, Bibcode:2005JPhA...38..869L, doi:10.1088/0305-4470/38/4/007.
- McKean, Henry P. (2003b), «The Liouville correspondence between the Korteweg–de Vries and the Camassa–Holm hierarchies», Comm. Pure Appl. Math. 56 (7): 998-1015, doi:10.1002/cpa.10083.
- Misiołek, Gerard (1998), «A shallow water equation as a geodesic flow on the Bott–Virasoro group», J. Geom. Phys. 24 (3): 203-208, Bibcode:1998JGP....24..203M, doi:10.1016/S0393-0440(97)00010-7.
Más lectura adicional
- Abenda, Simonetta; Grava, Tamara (2005), «Modulation of Camassa–Holm equation and reciprocal transformations», Annales de l'Institut Fourier 55 (6): 1803-1834, Bibcode:2005math.ph...6042A, arXiv:math-ph/0506042, doi:10.5802/aif.2142.
- Alber, Mark S.; Camassa, Roberto; Holm, Darryl D.; Marsden, Jerrold E. (1994), «The geometry of peaked solitons and billiard solutions of a class of integrable PDEs», Lett. Math. Phys. 32 (2): 137-151, Bibcode:1994LMaPh..32..137A, doi:10.1007/BF00739423.
- Alber, Mark S.; Camassa, Roberto; Holm, Darryl D.; Fedorov, Yuri N.; Marsden, Jerrold E. (2001), «The complex geometry of weak piecewise smooth solutions of integrable nonlinear PDE's of shallow water and Dym type», Comm. Math. Phys. 221 (1): 197-227, Bibcode:2001CMaPh.221..197A, arXiv:nlin/0105025, doi:10.1007/PL00005573.
- Artebrant, Robert; Schroll, Hans Joachim (2006), «Numerical simulation of Camassa–Holm peakons by adaptive upwinding», Applied Numerical Mathematics 56 (5): 695-711, doi:10.1016/j.apnum.2005.06.002.
- Beals, Richard; Sattinger, David H.; Szmigielski, Jacek (2005), «Periodic peakons and Calogero–Françoise flows», J. Inst. Math. Jussieu 4 (1): 1-27, doi:10.1017/S1474748005000010.
- Boutet de Monvel, Anne; Shepelsky, Dmitry (2005), «The Camassa–Holm equation on the half-line», C. R. Math. Acad. Sci. Paris 341 (10): 611-616, doi:10.1016/j.crma.2005.09.035.
- Boutet de Monvel, Anne; Shepelsky, Dmitry (2006), «Riemann–Hilbert approach for the Camassa–Holm equation on the line», C. R. Math. Acad. Sci. Paris 343 (10): 627-632, doi:10.1016/j.crma.2006.10.014.
- Boyd, John P. (2005), «Near-corner waves of the Camassa–Holm equation», Physics Letters A 336 (4–5): 342-348, Bibcode:2005PhLA..336..342B, doi:10.1016/j.physleta.2004.12.055.
- Byers, Peter (2006), «Existence time for the Camassa–Holm equation and the critical Sobolev index», Indiana Univ. Math. J. 55 (3): 941-954, doi:10.1512/iumj.2006.55.2710.
- Camassa, Roberto (2003), «Characteristics and the initial value problem of a completely integrable shallow water equation», Discrete Contin. Dyn. Syst. Ser. B 3 (1): 115-139, doi:10.3934/dcdsb.2003.3.115.
- Camassa, Roberto; Holm, Darryl D.; Hyman, J. M. (1994), «Advances in Applied Mechanics Volume 31», Adv. Appl. Mech., Advances in Applied Mechanics 31: 1-33, ISBN 9780120020317, doi:10.1016/S0065-2156(08)70254-0.
- Camassa, Roberto; Huang, Jingfang; Lee, Long (2005), «On a completely integrable numerical scheme for a nonlinear shallow-water wave equation», J. Nonlinear Math. Phys. 12 (suppl. 1): 146-162, Bibcode:2005JNMP...12S.146C, doi:10.2991/jnmp.2005.12.s1.13.
- Camassa, Roberto; Huang, Jingfang; Lee, Long (2006), «Integral and integrable algorithms for a nonlinear shallow-water wave equation», J. Comput. Phys. 216 (2): 547-572, Bibcode:2006JCoPh.216..547C, doi:10.1016/j.jcp.2005.12.013.
- Casati, Paolo; Lorenzoni, Paolo; Ortenzi, Giovanni; Pedroni, Marco (2005), «On the local and nonlocal Camassa–Holm hierarchies», J. Math. Phys. 46 (4): 042704, 8 pp, Bibcode:2005JMP....46d2704C, doi:10.1063/1.1888568.
- Coclite, Giuseppe Maria; Karlsen, Kenneth Hvistendahl (2006), «A singular limit problem for conservation laws related to the Camassa–Holm shallow water equation», Comm. Partial Differential Equations 31 (7–9): 1253-1272, doi:10.1080/03605300600781600.
- Coclite, Giuseppe Maria; Karlsen, Kenneth Hvistendahl; Risebro, Nils Henrik (2008a), «A convergent finite difference scheme for the Camassa–Holm equation with general H1 initial data», SIAM J. Numer. Anal. 46 (3): 1554-1579, doi:10.1137/060673242.
- Coclite, Giuseppe Maria; Karlsen, Kenneth Hvistendahl; Risebro, Nils Henrik (2008b), An explicit finite difference scheme for the Camassa–Holm equation.
- Cohen, David; Owren, Brynjulf; Raynaud, Xavier (2008), «Multi-symplectic integration of the Camassa–Holm equation», Journal of Computational Physics 227 (11): 5492-5512, Bibcode:2008JCoPh.227.5492C, doi:10.1016/j.jcp.2008.01.051.
- Constantin, Adrian (1997), «The Hamiltonian structure of the Camassa–Holm equation», Exposition. Math. 15 (1): 53-85.
- Constantin, Adrian (1998), «On the inverse spectral problem for the Camassa–Holm equation», J. Funct. Anal. 155 (2): 352-363, doi:10.1006/jfan.1997.3231.
- Constantin, Adrian (2005), «Finite propagation speed for the Camassa–Holm equation», J. Math. Phys. 46 (2): 023506, 4 pp, Bibcode:2005JMP....46b3506C, doi:10.1063/1.1845603.
- Constantin, Adrian; Escher, Joachim (1998a), «Global existence and blow-up for a shallow water equation», Ann. Scuola Norm. Sup. Pisa Cl. Sci. 26 (2): 303-328.
- Constantin, Adrian; Escher, Joachim (1998c), «Well-posedness, global existence, and blowup phenomena for a periodic quasi-linear hyperbolic equation», Comm. Pure Appl. Math. 51 (5): 475-504, doi:10.1002/(SICI)1097-0312(199805)51:5<475::AID-CPA2>3.0.CO;2-5.
- Constantin, Adrian; Gerdjikov, Vladimir S.; Ivanov, Rossen I. (2007), «Generalized Fourier transform for the Camassa–Holm hierarchy», Inverse Problems 23 (4): 1565-1597, Bibcode:2007InvPr..23.1565C, arXiv:0707.2048, doi:10.1088/0266-5611/23/4/012.
- Constantin, Adrian; Ivanov, Rossen (2006), «Poisson structure and action-angle variables for the Camassa–Holm equation», Lett. Math. Phys. 76 (1): 93-108, Bibcode:2006LMaPh..76...93C, arXiv:nlin/0602049, doi:10.1007/s11005-006-0063-9.
- Constantin, Adrian; Kolev, Boris (2003), «Geodesic flow on the diffeomorphism group of the circle», Comment. Math. Helv. 78 (4): 787-804, arXiv:math/0208076, doi:10.1007/s00014-003-0785-6.
- Constantin, Adrian; Molinet, Luc (2000), «Global weak solutions for a shallow water equation», Comm. Math. Phys. 211 (1): 45-61, Bibcode:2000CMaPh.211...45C, doi:10.1007/s002200050801.
- Constantin, Adrian; Molinet, Luc (2001), «Orbital stability of solitary waves for a shallow water equation», Phys. D 157 (1–2): 75-89, Bibcode:2001PhyD..157...75C, doi:10.1016/S0167-2789(01)00298-6.
- Dai, Hui-Hui (1998), «Model equations for nonlinear dispersive waves in a compressible Mooney–Rivlin rod», Acta Mech. 127 (1–4): 193-207, doi:10.1007/BF01170373.
- Dai, Hui-Hui; Pavlov, Maxim (1998), «Transformations for the Camassa–Holm equation, its high-frequency limit and the sinh-Gordon equation», J. Phys. Soc. Jpn. 67 (11): 3655-3657, Bibcode:1998JPSJ...67.3655D, doi:10.1143/JPSJ.67.3655.
- Danchin, Raphaël (2001), «A few remarks on the Camassa–Holm equation», Differential Integral Equations 14 (8): 953-988.
- Danchin, Raphaël (2003), «A note on well-posedness for Camassa–Holm equation», J. Differential Equations 192 (2): 429-444, Bibcode:2003JDE...192..429D, doi:10.1016/S0022-0396(03)00096-2.
- Escher, Joachim; Yin, Zhaoyang (2008), «Initial boundary value problems of the Camassa–Holm equation», Comm. Partial Differential Equations 33 (1–3): 377-395, doi:10.1080/03605300701318872.
- Fisher, Michael; Schiff, Jeremy (1999), «The Camassa–Holm equation: conserved quantities and the initial value problem», Phys. Lett. A 259 (5): 371-376, Bibcode:1999PhLA..259..371F, arXiv:solv-int/9901001, doi:10.1016/S0375-9601(99)00466-1.
- Fuchssteiner, Benno (1981), «The Lie algebra structure of nonlinear evolution equations admitting infinite-dimensional abelian symmetry groups», Progr. Theoret. Phys. 65 (3): 861-876, Bibcode:1981PThPh..65..861F, doi:10.1143/PTP.65.861.
- Fuchssteiner, Benno; Fokas, Athanassios S. (1981–82), «Symplectic structures, their Bäcklund transformations and hereditary symmetries», Physica D 4 (1): 47-66, Bibcode:1981PhyD....4...47F, doi:10.1016/0167-2789(81)90004-X.
- Gesztesy, Fritz; Holden, Helge (2003), «Algebro-geometric solutions of the Camassa–Holm hierarchy», Rev. Mat. Iberoamericana 19 (1): 73-142.
- Golovko, V.; Kersten, P.; Krasilʹshchik, I.; Verbovetsky, A. (2008), «On integrability of the Camassa–Holm equation and its invariants: a geometrical approach», Acta Appl. Math. 101 (1–3): 59-83, arXiv:0812.4681, doi:10.1007/s10440-008-9200-z.
- Himonas, A. Alexandrou; Misiołek, Gerard (2001), «The Cauchy problem for an integrable shallow-water equation», Differential and Integral Equations 14 (7): 821-831.
- Himonas, A. Alexandrou; Misiołek, Gerard (2005), «High-frequency smooth solutions and well-posedness of the Camassa–Holm equation», Int. Math. Res. Not. 2005 (51): 3135-3151, doi:10.1155/IMRN.2005.3135.
- Himonas, A. Alexandrou; Misiołek, Gerard; Ponce, Gustavo; Zhou, Yong (2007), «Persistence properties and unique continuation of solutions of the Camassa–Holm equation», Comm. Math. Phys. 271 (2): 511-522, Bibcode:2007CMaPh.271..511H, arXiv:math/0604192, doi:10.1007/s00220-006-0172-4.
- Holden, Helge; Raynaud, Xavier (2006a), «A convergent numerical scheme for the Camassa–Holm equation based on multipeakons», Discrete Contin. Dyn. Syst. 14 (3): 505-523, doi:10.3934/dcds.2006.14.505.
- Holden, Helge; Raynaud, Xavier (2006b), «Convergence of a finite difference scheme for the Camassa–Holm equation», SIAM J. Numer. Anal. 44 (4): 1655-1680, doi:10.1137/040611975.
- Holden, Helge; Raynaud, Xavier (2008a), «Periodic conservative solutions of the Camassa–Holm equation», Annales de l'Institut Fourier 58 (3): 945-988, doi:10.5802/aif.2375.
- Holden, Helge; Raynaud, Xavier (2007b), «Global conservative solutions of the Camassa–Holm equation—a Lagrangian point of view», Communications in Partial Differential Equations 32 (10–12): 1511-1549, doi:10.1080/03605300601088674.
- Holden, Helge; Raynaud, Xavier (2008), Dissipative solutions for the Camassa–Holm equation.
- Hwang, Seok (2007), «Singular limit problem of the Camassa–Holm type equation», Journal of Differential Equations 235 (1): 74-84, Bibcode:2007JDE...235...74H, doi:10.1016/j.jde.2006.12.011.
- Ionescu-Kruse, Delia (2007), «Variational derivation of the Camassa–Holm shallow water equation with non-zero vorticity», Discrete Contin. Dyn. Syst. 19 (3): 531-543, Bibcode:2007arXiv0711.4701I, arXiv:0711.4701, doi:10.3934/dcds.2007.19.531, archivado desde el original el 3 de marzo de 2016, consultado el 28 de mayo de 2019.
- Johnson, Robin S. (2002), «Camassa–Holm, Korteweg–de Vries and related models for water waves», J. Fluid Mech. 455 (1): 63-82, Bibcode:2002JFM...455...63J, doi:10.1017/S0022112001007224.
- Johnson, Robin S. (2003a), «The Camassa–Holm equation for water waves moving over a shear flow», Fluid Dynam. Res. 33 (1–2): 97-111, Bibcode:2003FlDyR..33...97J, doi:10.1016/S0169-5983(03)00036-4.
- Johnson, Robin S. (2003c), «On solutions of the Camassa–Holm equation», R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 459 (2035): 1687-1708, Bibcode:2003RSPSA.459.1687J, doi:10.1098/rspa.2002.1078.
- Kaup, D. J. (2006), «Evolution of the scattering coefficients of the Camassa–Holm equation, for general initial data», Stud. Appl. Math. 117 (2): 149-164, doi:10.1111/j.1467-9590.2006.00350.x.
- Khesin, Boris; Misiołek, Gerard (2003), «Euler equations on homogeneous spaces and Virasoro orbits», Advances in Mathematics 176 (1): 116-144, arXiv:math/0210397, doi:10.1016/S0001-8708(02)00063-4.
- de Lellis, Camillo; Kappeler, Thomas; Topalov, Peter (2007), «Low-regularity solutions of the periodic Camassa–Holm equation», Communications in Partial Differential Equations 32 (1–3): 87-126, doi:10.1080/03605300601091470.
- Lenells, Jonatan (2004), «A variational approach to the stability of periodic peakons», J. Nonlinear Math. Phys. 11 (2): 151-163, Bibcode:2004JNMP...11..151L, doi:10.2991/jnmp.2004.11.2.2.
- Lenells, Jonatan (2004), «Stability of periodic peakons», International Mathematics Research Notices 2004 (10): 485-499, doi:10.1155/S1073792804132431.
- Lenells, Jonatan (2004), «The correspondence between KdV and Camassa–Holm», International Mathematics Research Notices 2004 (71): 3797-3811, doi:10.1155/S1073792804142451.
- Lenells, Jonatan (2005), «Stability for the periodic Camassa–Holm equation», Mathematica Scandinavica 97 (2): 188-200, doi:10.7146/math.scand.a-14971, archivado desde el original el 22 de diciembre de 2008, consultado el 28 de mayo de 2019.
- Lenells, Jonatan (2007), «Infinite propagation speed of the Camassa–Holm equation», J. Math. Anal. Appl. 325 (2): 1468-1478, doi:10.1016/j.jmaa.2006.02.045.
- Li, Luen-Chau (2008), «Factorization problem on the Hilbert–Schmidt group and the Camassa–Holm equation», Comm. Pure Appl. Math. 61 (2): 186-209, arXiv:math/0601156, doi:10.1002/cpa.20207.
- Lombardo, Maria Carmela; Sammartino, Marco; Sciacca, Vincenzo (2005), «A note on the analytic solutions of the Camassa–Holm equation», C. R. Math. Acad. Sci. Paris 341 (11): 659-664, doi:10.1016/j.crma.2005.10.006.
- Loubet, Enrique (2006), «Genesis of solitons arising from individual flows of the Camassa–Holm hierarchy», Comm. Pure Appl. Math. 59 (3): 408-465, doi:10.1002/cpa.20109.
- Misiołek, Gerard (2005), «Classical solutions of the periodic Camassa–Holm equation», Geometric and Functional Analysis 12 (5): 1080-1104, doi:10.1007/PL00012648.
- Olver, Peter J.; Rosenau, Philip (1996), «Tri-Hamiltonian duality between solitons and solitary-wave solutions having compact support», Phys. Rev. E 53 (2): 1900-1906, Bibcode:1996PhRvE..53.1900O, doi:10.1103/PhysRevE.53.1900.
- Ortenzi, Giovanni; Pedroni, Marco; Rubtsov, Vladimir (2008), «On the higher Poisson structures of the Camassa–Holm hierarchy», Acta Appl. Math. 101 (1–3): 243-254, doi:10.1007/s10440-008-9188-4.
- Parker, Allen (2004), «On the Camassa–Holm equation and a direct method of solution. I. Bilinear form and solitary waves», Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 460 (2050): 2929-2957, Bibcode:2004RSPSA.460.2929P, doi:10.1098/rspa.2004.1301.
- Parker, Allen (2005), «On the Camassa–Holm equation and a direct method of solution. II. Soliton solutions», Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 461 (2063): 3611-3632, Bibcode:2005RSPSA.461.3611P, doi:10.1098/rspa.2005.1536.
- Parker, Allen (2006), «A factorization procedure for solving the Camassa–Holm equation», Inverse Problems 22 (2): 599-609, Bibcode:2006InvPr..22..599P, doi:10.1088/0266-5611/22/2/013.
- Parker, Allen (2007), «Cusped solitons of the Camassa–Holm equation. I. Cuspon solitary wave and antipeakon limit», Chaos, Solitons & Fractals 34 (3): 730-739, Bibcode:2007CSF....34..730P, doi:10.1016/j.chaos.2007.01.033.
- Parker, Allen (2008), «Wave dynamics for peaked solitons of the Camassa–Holm equation», Chaos, Solitons & Fractals 35 (2): 220-237, Bibcode:2008CSF....35..220P, doi:10.1016/j.chaos.2007.07.049.
- Qiao, Zhijun (2003), «The Camassa–Holm hierarchy, N-dimensional integrable systems, and algebro-geometric solution on a symplectic submanifold», Communications in Mathematical Physics 239 (1–2): 309-341, Bibcode:2003CMaPh.239..309Q, doi:10.1007/s00220-003-0880-y.
- Rodríguez-Blanco, Guillermo (2001), «On the Cauchy problem for the Camassa–Holm equation», Nonlinear Analysis 46 (3): 309-327, doi:10.1016/S0362-546X(01)00791-X.
- Schiff, Jeremy (1998), «The Camassa–Holm equation: a loop group approach», Physica D 121 (1–2): 24-43, Bibcode:1998PhyD..121...24S, arXiv:solv-int/9709010, doi:10.1016/S0167-2789(98)00099-2.
- Vaninsky, K. L. (2005), «Equations of Camassa–Holm type and Jacobi ellipsoidal coordinates», Communications on Pure and Applied Mathematics 58 (9): 1149-1187, arXiv:math-ph/0303063, doi:10.1002/cpa.20089.
- Wahlén, Erik (2005), «A blow-up result for the periodic Camassa–Holm equation», Archiv der Mathematik 84 (4): 334-340, doi:10.1007/s00013-004-1199-4.
- Wahlén, Erik (2006), «Global existence of weak solutions to the Camassa–Holm equation», Int. Math. Res. Not. 2006: Art. ID 28976, 12 pp, doi:10.1155/IMRN/2006/28976.
- Wu, Shuyin; Yin, Zhaoyang (2006), «Blow-up, blow-up rate and decay of the solution of the weakly dissipative Camassa–Holm equation», J. Math. Phys. 47 (1): 013504, 12 pp, Bibcode:2006JMP....47a3504W, doi:10.1063/1.2158437.
- Xin, Zhouping; Zhang, Ping (2002), «On the uniqueness and large time behavior of the weak solutions to a shallow water equation», Comm. Partial Differential Equations 27 (9–10): 1815-1844, doi:10.1081/PDE-120016129.
- Zampogni, Luca (2007), «On algebro-geometric solutions of the Camassa–Holm hierarchy», Adv. Nonlinear Stud. 7 (3): 345-380, doi:10.1515/ans-2007-0303.