Eneágono
En geometría, un eneágono o nonágono es un polígono de nueve lados y nueve vértices. El nombre proviene del griego enneagonon, (εννεα, nueve + γωνον, esquina), mientras que nonágono proviene del latín (nonus, nueve + gonon ).
| Eneágono | ||
|---|---|---|
 Un eneágono regular | ||
| Características | ||
| Tipo | Polígono regular | |
| Lados | 9 | |
| Vértices | 9 | |
| Grupo de simetría | , orden 2x9 | |
| Diagrama de Coxeter-Dynkin |
| |
| Polígono dual | Autodual | |
| Área | ||
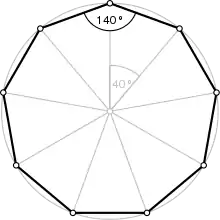
| Ángulo interior | 140° | |
| Propiedades | ||
| Convexo, isogonal, cíclico | ||
Construcción
Es posible construir un eneágono regular inscrito en un círculo con regla y compás de forma aproximada. De otro modo, es necesario utilizar un transportador, gnómon u otro método tal como software especializado en geometría o técnicas trigonométricas y algebraica.

Propiedades
Un eneágono tiene 27 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número total de diagonales de un polígono, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle D=n(n-3)/2} ; siendo el número de lados , tenemos:
La suma de todos los ángulos internos de cualquier eneágono es 1260 grados o Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle 7\pi} radianes.
Eneágono regular
Un eneágono regular es aquel polígono regular de nueve lados que tiene todos sus lados de la misma longitud y todos sus ángulos internos iguales. Cada ángulo interno del eneágono regular mide 140° o rad. Cada ángulo externo del eneágono regular mide 40º o rad.
Al multiplicar la longitud t de un lado de un eneágono regular por nueve (el número de lados n del polígono) obtendremos la longitud de su perímetro P.
El área de un eneágono regular de lado t puede calcularse de la siguiente forma:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle A = \frac{9t^2}{4\tan(\frac{\pi}{9})}\simeq 6.1818\ t^2,}
donde es la constante pi y es la función tangente calculada en radianes. O bien, si se conoce la apotema, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle a_p} ,[1]
Si se conoce la longitud de la apotema, , y el lado, , otra alternativa para calcular el área es:
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle A = \frac{P\cdot a_p}{2} = \frac{9\cdot t\cdot a_p}{2}}
Véase también
Referencias
- Sapiña, R. «Calculadora del área y perímetro del eneágono regular». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 22 de junio de 2020.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre eneágonos.
Wikimedia Commons alberga una categoría multimedia sobre eneágonos. Wikcionario tiene definiciones y otra información sobre eneágono.
Wikcionario tiene definiciones y otra información sobre eneágono.- Weisstein, Eric W. «Eneágono». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.