Error absoluto medio

Dadas dos series de datos (X e Y) relativas a un mismo fenómeno, considérese un diagrama de dispersión de n puntos, donde el punto i tiene coordenadas (x_i, y_i). El error absoluto medio (EAM) es la distancia vertical promedio entre cada uno de los puntos y la recta identidad (y=x), o también la distancia horizontal promedio entre cada punto y la recta identidad.

Viene dado por:[1]

${\displaystyle \mathrm {EAM} ={\frac {\sum _{i=1}^{n}\left|y_{i}-x_{i}\right|}{n}}={\frac {\sum _{i=1}^{n}\left|e_{i}\right|}{n}}.}$

Este indicador tiene una interpretación clara como la diferencia absoluta promedio entre y_i y x_i. Es un dato habitualmente utilizado por su sencillez conceptual, pero con frecuencia se confunde con la raíz del error cuadrático medio, diferente del error absoluto promedio.[1][2]

Como su nombre indica, el error absoluto medio es un promedio de los errores absolutos ${\displaystyle |e_{i}|=|y_{i}-x_{i}|}$, donde ${\displaystyle y_{i}}$ es la predicción y ${\displaystyle x_{i}}$ el valor verdadero. Téngase en cuenta que las formulaciones alternativas pueden incluir frecuencias relativas como factores de ponderación. El error absoluto medio utiliza la misma escala que los datos que se están midiendo. Esto se conoce como una medida de precisión dependiente de la escala y, por lo tanto, no se puede usar para hacer comparaciones entre series que usan diferentes escalas.[3] El error absoluto promedio es una medida común del error de predicción en series temporales,[4] aunque a veces se confunde con la definición más estándar de desviación media.

2 puntos de datos para los cuales el error de cantidad es 0 y el error de localización es 2 para el error absoluto medio y para el error cuadrático medio

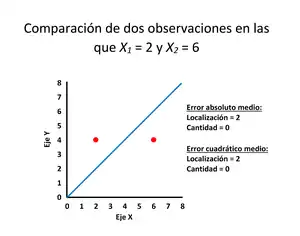
Es posible expresar el error absoluto medio como la suma de dos componentes: desajuste de cantidad y desajuste de asignación. El desajuste de cantidad es el valor absoluto del error medio, dado por:[5]

${\displaystyle \mathrm {EM} ={\frac {\sum _{i=1}^{n}y_{i}-x_{i}}{n}}}$

El desajuste de asignación es el EMA menos el desajuste de cantidad.

También es posible identificar los tipos de diferencia observando un gráfico ${\displaystyle (x,y)}$. La diferencia de cantidad existe cuando el promedio de los valores de X no es igual al promedio de los valores de Y. La diferencia de asignación existe si y solo si los puntos se sitúan a ambos lados de la recta identidad.[5][2]

El error absoluto medio es una de las distintas maneras de comparar los pronósticos con los resultados finales. Las alternativas bien establecidas son el error escalado absoluto medio (EEAM) y el error cuadrático medio. Todos ellos resumen el resultado de manera que no tienen en cuenta el sentido de la predicción (por exceso o por defecto). Una medida que considera este aspecto es la diferencia con signo media.

Cuando se debe ajustar un modelo de predicción utilizando una medida del ajuste obtenido (en el sentido en que el enfoque de los mínimos cuadrados está relacionado con el error cuadrático medio), el equivalente del error absoluto medio son las mínimas desviaciones absolutas.

El error absoluto medio no es idéntico al error cuadrático medio, aunque en ocasiones se confundan. El primero es conceptualmente más simple y más interpretable, y no requiere el uso de cuadrados o de raíces cuadradas, siendo simplemente la distancia vertical u horizontal absoluta promedio entre cada punto en un diagrama de dispersión y la línea Y = X. En otras palabras, es la diferencia absoluta promedio entre X e Y. Además, cada error contribuye en proporción a su valor absoluto, lo que no es cierto para las estimaciones cuadráticas.[5]

• Mínimas desviaciones absolutas
• Error porcentual absoluto medio
• Error porcentual medio
• Error porcentual absoluto medio simétrico