Escalera de distancias cósmicas
Se denomina escalera de distancias cósmicas a la sucesión de distintos métodos para realizar medidas de la distancia a objetos cada vez más lejanos. Cada uno de los métodos se basa en uno o más métodos de medida para distancias menores, lo que puede verse como los distintos pasos o peldaños de una escalera. Para avanzar un peldaño en la escalera es necesario haberse apoyado antes en el peldaño anterior.

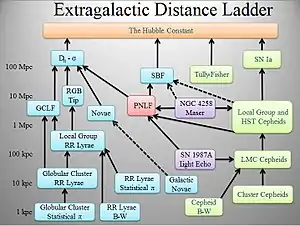
Es imposible realizar medidas directas de distancias para objetos a más de 1000 pc de distancia. A partir de estas distancias se tienen que asumir ciertos modelos físicos como base para los sistemas de medida. Los primeros modelos, para distancias ligeramente superiores, deben ser calibrados con los métodos directos. A partir de aquí cada método se va apoyando en los anteriores, aumentándose de esta manera el alcance de las medidas.
Métodos geométricos

Algunos métodos de medida hacen uso solamente de la configuración geométrica del objeto astronómico. En general estos métodos requieren la observación de movimientos tangenciales y radiales a la línea de visión. Los movimientos radiales se miden con gran precisión con el desplazamiento Doppler de las líneas espectrales de un objeto. La medida de los movimientos tangenciales es muy complicada debido a la gran distancia a la que se encuentran los objetos. En muchos casos se requieren satélites fuera de la atmósfera terrestre o técnicas especiales como la radiointerferometría para alcanzar la suficiente resolución angular.
Paralaje trigonométrico
Para medir la distancia a las estrellas cercanas se usa la paralaje astronómica. La paralaje es el cambio en la posición aparente de una estrella en el cielo debido al movimiento de la Tierra en su órbita alrededor del Sol. Las estrellas más lejanas parecen fijas mientras que las cercanas se mueven en una elipse más o menos excéntrica dependiendo del ángulo relativo de la estrella con respecto a la eclíptica. La distancia obtenida con este método viene dada en función del ángulo medido y de la distancia de la Tierra al Sol (Unidad astronómica), así que su precisión depende directamente de la precisión de las dos medidas anteriores. El satélite Hipparcos midió sistemáticamente entre 1989 y 1993 la paralaje de 2,5 millones de estrellas, medidas con las que se pudieron estimar muchas de sus distancias.
Método del cúmulo móvil
Los cúmulos abiertos son agrupaciones de estrellas que han nacido de forma prácticamente simultánea de una misma nube molecular. Estas agrupaciones se mantienen unidas durante cierto tiempo antes de dispersarse y se mueven con la misma velocidad. Se puede usar un método puramente geométrico utilizando estas propiedades para determinar su distancia, con el denominado método del cúmulo móvil.
Distancia al centro galáctico y a la nebulosa del Cangrejo
En la zona cercana al centro de nuestra galaxia se pueden observar máseres de agua en radio. La velocidad radial de estos máseres se puede determinar con mucha precisión a partir del desplazamiento Doppler de la emisión. La velocidad tangencial se mide usando radiointerferometría de muy larga base. Se asume que los máseres se expanden esféricamente desde un punto central común. Con este modelo y las velocidades se puede determinar la distancia. Por ejemplo, la distancia a la que se estimó que se encontraba el centro de la galaxia usando este método fue de 7500 ± 1500 pc (24.000 ± 5000 años luz). [3]
En el caso de la nebulosa del Cangrejo se puede observar el mismo efecto de expansión anterior tanto radial como tangencialmente. Con los datos medidos se estimó una distancia de unos 6.300 años luz. [4]
Candelas estándar
Cuando no es posible utilizar un método geométrico se usan las denominadas candelas estándar para medir la distancia. Las candelas estándar son objetos astronómicos que tienen una luminosidad o una propiedad conocida que permite usarlas para medir su distancia. Estos objetos deben poder reconocerse a partir de alguna característica como, por ejemplo, una variabilidad temporal específica o alguna característica de su espectro electromagnético. Además, dependiendo de la mayor o menor luminosidad de la candela podrá observarse, y por lo tanto poderse medir, hasta distancias mayores o menores.
Para poder usar un objeto de luminosidad conocida como candela estándar hay que calibrar su luminosidad intrínseca. Si se conoce el flujo (f) que se recibe del objeto y su distancia (d), por uno de los métodos directos explicados anteriormente, se puede calcular su luminosidad con la siguiente relación:
se obtiene la luminosidad, que es una propiedad independiente de la distancia, de esa candela. En algunos objetos usados como candelas estándar la luminosidad varía con el tiempo pero siempre de una forma conocida.
En el caso de que no se pudiera estimar con métodos geométricos la distancia a la candela, se usaría la distancia estimada a partir de una candela de diferente clase. De esta manera se van alcanzando cada vez distancias más grandes.
Ajuste al diagrama de Hertzsprung-Russell
Las estrellas se pueden clasificar, según sus propiedades espectrales y de luminosidad, dentro del diagrama de Hertzsprung-Russell. Un grupo de estrellas como, por ejemplo, un cúmulo abierto presenta una distribución de estrellas que encaja en el diagrama anterior. El diagrama se expresa en luminosidades o magnitudes absolutas, mientras que lo que se observa desde la Tierra es la magnitud aparente de las estrellas. La magnitud absoluta (M) se relaciona con la magnitud aparente (m) observada con esta relación:
El método consiste en ajustar la distancia promedio para todas las estrellas que hace que la distribución se ajuste al diagrama.
Variables RR Lyrae
Las estrellas variables del tipo RR Lyrae son un prototipo de estrellas variables que reciben su nombre genérico de la estrella RR Lyrae. Se suelen encontrar en gran cantidad en cúmulos de estrellas. Su luminosidad (o su magnitud absoluta) se conoce con exactitud. Comparándola con su magnitud aparente, se puede estimar la distancia a la que se encuentran.
Variables Cefeidas
Las estrellas variables Cefeidas son estrellas variables muy luminosas. Aunque su luminosidad varía cíclicamente, presentan una relación muy precisa entre su luminosidad y su periodo:
siendo el periodo en días y Mv la magnitud absoluta. [5]
Las Cefeidas pueden observarse en algunas galaxias cercanas a la Vía Láctea con lo que se puede determinar su distancia.
Sirena estándar
Las ondas gravitacionales que se originan en la fase de colapso de los sistemas binarios compactos, como las estrellas de neutrones o los agujeros negros, tienen la propiedad útil de que tanto la amplitud como la forma de la radiación gravitatoria emitida dependen fuertemente de la masa de chirrido del sistema. Al observar la forma de onda, se puede calcular la masa de este chirrido, y por lo tanto, su amplitud. Además, las ondas gravitacionales no están sujetas a la extinción debido a un medio intermedio absorbente (aunque están sujetas a lentes gravitacionales). Por lo tanto, una fuente de ondas gravitacionales de este tipo es una "sirena estándar" de volumen conocido.[6]
La relación entre la fuente y las amplitudes recibidas permite calcular su distancia. Por lo tanto, una sirena estándar se puede usar como un indicador de distancia en una escala cósmica. Cuando la colisión se puede observar ópticamente también (como en el caso de una kilonova), se puede medir el desplazamiento Doppler y calcular la constante de Hubble.[7]
Candelas estándar extragalácticas
Relaciones de Tully-Fisher y Faber-Jackson
La relación de Tully-Fisher es la relación empírica que se observa en galaxias espirales entre su luminosidad y su curva de rotación. Se suele medir la anchura de la línea de HI en 21 cm, ya que muestrea bien la curva de rotación hasta distancias lo suficientemente alejadas del centro. [8]
La relación de Faber-Jackson es una relación parecida a la anterior, pero que se observa en galaxias elípticas. También expresa una relación entre la luminosidad y la dispersión de velocidades de las estrellas. [9] La versión mejorada que se usa de esta relación incluye la extensión angular de la galaxia y se denomina D-σ.
Fluctuación del brillo superficial
Las galaxias siguen unos perfiles de brillo superficial bien conocidos. La presencia de estrellas gigantes muy luminosas en la galaxia hace que aparezcan pequeñas fluctuaciones en este brillo superficial. Si se considera una distribución de estrellas más o menos homogénea en la superficie de la galaxia, en una región de superficie angular definida habrá más o menos variación dependiendo del número de estrellas gigantes que caigan dentro. La cantidad de estrellas que caigan dependerá de la distancia a la que se encuentre la galaxia. Usando estadística de Poisson en las fluctuaciones del brillo superficial se puede estimar el número de estrellas por unidad de superficie y deducir, en función de este número, la distancia a la galaxia.
Funciones de luminosidad
Con este método se determina la distribución típica de luminosidades de algún tipo de objeto astronómico. Ajustando la luminosidad de la distribución con la magnitud observada se obtiene un indicador de la distancia. En general las funciones de luminosidad más usadas para estimar las distancias son las de nebulosas planetarias, cúmulos globulares y las regiones HII.
Supernovas tipo Ia
Las supernovas de tipo Ia son muy luminosas y pueden observarse en cualquier tipo de galaxia. Tienen una curva de luz muy bien caracterizada con lo que permiten estimar la distancia a la galaxia donde se produce la supernova.
Ley de Hubble
La ley de Hubble indica que el desplazamiento al rojo de la emisión de una galaxia es proporcional a la distancia a la que se encuentra. Este método de medida de distancias debe ser calibrado con los métodos anteriores. Las pequeñas variaciones locales de la velocidad de una galaxia nos llevan a tener cierta incertidumbre cuando se usa este método. Debido a la relativa facilidad para observar espectros de objetos lejanos, es el método más universal, y en muchos casos el único, que existe para realizar medidas a objetos lejanos.
Referencias
- «Hubble finds Universe may be expanding faster than expected» (en inglés). Consultado el 3 de junio de 2016.
- «Hubble stretches the stellar tape measure ten times further». ESA/Hubble Images (en inglés). Consultado el 12 de abril de 2014.
- Reid, M. J.; Schneps, M. H.; Moran, J. M.; Gwinn, C. R.; Genzel, R.; Downes, D.; Roennaeng, B. (1988). «The distance to the center of the Galaxy - H2O maser proper motions in Sagittarius B2(N)». Astrophysical Journal (en inglés) 330. 809-816.
- Trimble, Virginia (1973). «The Distance to the Crab Nebula and NP 0532». Publications of the Astronomical Society of the Pacific 85 (507). 579.
- Feast, M. W.; Catchpole, R. M. (1997). «The Cepheid period-luminosity zero-point from HIPPARCOS trigonometrical parallaxes». Monthly Notices of the Royal Astronomical Society (en inglés) 286 (1). L1.
- Hendry, Martin; Woan, Graham (February 2007). «Gravitational astrophysics». Astronomy & Geophysics (en inglés) 48 (1): 1.10-1.17. doi:10.1111/j.1468-4004.2007.48110.x. Consultado el 16 de octubre de 2017.
- Abbott, B. P. (16 de octubre de 2017). «A gravitational-wave standard siren measurement of the Hubble constant». Nature (en inglés). arXiv:1710.05835. doi:10.1038/nature24471. «LIGO Scientific Collaboration & Virgo Collaboration ».
- Tully, R. B.; Fisher, J. R. (1977). «A new method of determining distances to galaxies». Astronomy and Astrophysics (en inglés) 54 (3). 661.
- Faber, S. M.; Jackson, R. E. (1976). «Velocity dispersions and mass-to-light ratios for elliptical galaxies». Astrophysical Journal (en inglés) 204 (1). 668.
Bibliografía
- Bradt, Hale (2004). Astronomy Methods. A Physical Approach to Astronomical Observations (en inglés) (1ª edición). Cambridge: Cambridge University Press. ISBN 978-0-521-53551-9.
- Measuring the Universe The Cosmological Distance Ladder, Stephen Webb, copyright 2001. (en inglés)
- Pasachoff, J.M.; Filippenko, A. (2013). The Cosmos: Astronomy in the New Millennium (en inglés) (4th edición). Cambridge: Cambridge University Press. ISBN 978-1-107-68756-1.
- The Astrophysical Journal, The Globular Cluster Luminosity Function as a Distance Indicator: Dynamical Effects, Ostriker and Gnedin, May 5, 1997. (en inglés)
- An Introduction to Distance Measurement in Astronomy, Richard de Grijs, Chichester: John Wiley & Sons, 2011, ISBN 978-0-470-51180-0. (en inglés)
- Bożena Czerny; Rachael Beaton; Michał Bejger; Edward Cackett; Massimo Dall’Ora et al. (febrero 2018). «Astronomical Distance Determination in the Space Age, Secondary Distance Indicators». Space Science Reviews (en inglés) 214 (32). doi:10.1007/s11214-018-0466-9. Consultado el 23 de marzo de 2018.
Bibliografía adicional
- Ash, M. E.; Shapiro, I. I.; Smith, W. B. (1967). «Astronomical constants and planetary ephemerides deduced from radar and optical observations». The Astronomical Journal (en inglés) 72: 338. Bibcode:1967AJ.....72..338A. doi:10.1086/110230.
Enlaces externos
- The ABC's of distances (UCLA) (en inglés)
- The Extragalactic Distance Scale by Bill Keel (en inglés)
- The Hubble Space Telescope Key Project on the Extragalactic Distance Scale (en inglés)
- The Hubble Constant, a historical discussion (en inglés)
- NASA Cosmic Distance Scale (en inglés)
- PNLF information database (en inglés) Archivado el 26 de enero de 2010 en Wayback Machine.
- The Astrophysical Journal (en inglés)