Espacio cociente (álgebra lineal)
En álgebra lineal, el espacio vectorial cociente E/F de un espacio vectorial E por un subespacio vectorial F, es la estructura natural de espacio vectorial sobre el conjunto cociente de E por la siguiente relación de equivalencia: v está relacionado con w si y solo si v-w pertenece a F.
Definición
Sea E un espacio vectorial sobre un cuerpo K, y sea F un subespacio vectorial de E, podemos definir la siguiente relación de equivalencia entre los elementos de E:
Dados diremos que están relacionados módulo si .
| La relación anterior es una relación de equivalencia |
Se considera la relación y se comprueban:
|
Observación: equivale a , es decir, y abusando del lenguaje
- Se nota por a la clase de módulo .
Llamaremos espacio cociente al conjunto de todos los elementos que cumplen las clases de equivalencia anterior:
- Se nota por a dicho espacio cociente.
El espacio es un espacio vectorial con las operaciones siguientes:
|
|
La suma y multiplicación están definidas por ser un subespacio vectorial:
|
Observaciones
- Si , por constituir una partición de
- Si
- Si ,
- Los elementos de no son un espacio vectorial en pues no tiene el elemento neutro
- Esta estructura vectorial es la única en el cociente que hace a la proyección canónica lineal.
Dimensión del espacio cociente
Dado un espacio vectorial y un subespacio, si la dimensión de E es finita entonces:
|
Sean , y una base de Se puede completar la base hasta obtener una de , .
Tomando clases, , pues (ya que ). Luego, se tiene que generan Para ver que son linealmente independientes, supóngase que:
entonces, pertenece a , en consecuencia, existen tales que . Por la independencia lineal de , se sigue que . Por lo tanto, son una base de y |
Ejemplo
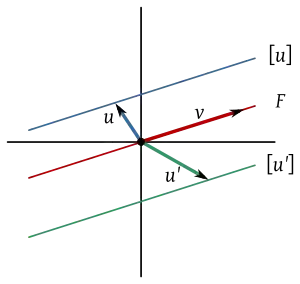
Sea un subespacio vectorial de generado por un vector , , si se considera el espacio cociente la clase de un vector será:
- , siendo su espacio cociente , es decir todas las rectas paralelas al subespacio F.
Referencias
- Weisstein, Eric W. «Espacio Vectorial Cociente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Bibliografía
- Manuel Castellet, Irene Llerena, Álgebra lineal y geometría, Editorial reverté, S.A., 2000.