Espacio de probabilidad

Espacio de probabilidad para lanzar un dado dos veces seguidas: El espacio muestral ${\displaystyle \Omega }$ consta de los 36 resultados posibles; se muestran tres sucesos diferentes (polígonos coloreados), con sus respectivas probabilidades (suponiendo una distribución uniforme discreta

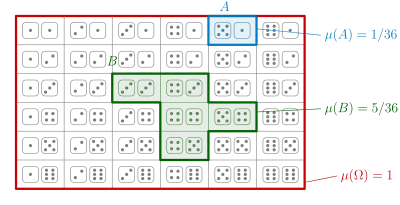
Un espacio de probabilidad es un triplete matemático ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ que presenta un modelo para una clase particular de situaciones del mundo real. Como ocurre con otros modelos, su autor define en última instancia qué elementos contendrán ${\displaystyle \Omega }$, ${\displaystyle {\cal {F}}}$, y ${\displaystyle P}$.

• El espacio muestral ${\displaystyle \Omega }$ es el conjunto de todos los resultados posibles. Un resultado es el resultado de una única ejecución del modelo. Los resultados pueden ser estados de la naturaleza, posibilidades, resultados experimentales y similares. Cada instancia de la situación del mundo real (o ejecución del experimento) debe producir exactamente un resultado. Si los resultados de diferentes ejecuciones de un experimento difieren de alguna manera importante, son resultados distintos. Qué diferencias son importantes depende del tipo de análisis que queramos hacer. Esto conduce a diferentes opciones de espacio muestral.
• El σ-álgebra ${\displaystyle {\mathcal {F}}}$ es una colección de todos los eventos que nos gustaría considerar. Esta colección puede o no incluir cada uno de los elemental. Aquí, un "suceso" es un conjunto de cero o más resultados; es decir, un subconjunto del espacio muestral. Se considera que un suceso ha "ocurrido" durante un experimento cuando el resultado de éste es un elemento del suceso. Dado que el mismo resultado puede ser miembro de muchos sucesos, es posible que hayan ocurrido muchos sucesos dado un único resultado. Por ejemplo, cuando el ensayo consiste en lanzar dos dados, el conjunto de todos los resultados con una suma de 7 pips puede constituir un suceso, mientras que los resultados con un número impar de pips pueden constituir otro suceso. Si el resultado es el elemento del suceso elemental de dos pepitas en el primer dado y cinco en el segundo, entonces se dice que ambos sucesos, "7 pepitas" y "número impar de pepitas", han ocurrido.
• La medida de probabilidad ${\displaystyle P}$ es una función de conjunto que devuelve la probabilidad de un suceso. Una probabilidad es un número real entre cero (los sucesos imposibles tienen probabilidad cero, aunque los sucesos con probabilidad cero no son necesariamente imposibles) y uno (el suceso ocurre casi con seguridad, con casi total certeza). Así, ${\displaystyle P}$ es una función ${\displaystyle P:{\mathcal {F}}\to [0,1].}$ La función de medida de la probabilidad debe satisfacer dos simples requisitos: En primer lugar, la probabilidad de la unión de un contable de sucesos mutuamente excluyentes debe ser igual a la suma contable de las probabilidades de cada uno de estos sucesos. Por ejemplo, la probabilidad de la unión de los sucesos mutuamente excluyentes ${\displaystyle texto{cabeza}}$ y ${\displaystyle texto{cola}}$ en el experimento aleatorio de un lanzamiento de moneda, ${\displaystyle P({\text{Cabeza}}\cup {\text{Cola}})}$, es la suma de la probabilidad para ${\displaystyle {\text{Cabeza}}}$ y la probabilidad para ${\displaystyle {\text{Cola}}}$, ${\displaystyle P({\text{Cabeza}})+P({\text{Cola}})}$. En segundo lugar, la probabilidad del espacio muestral ${\displaystyle \Omega }$ debe ser igual a 1 (lo que da cuenta del hecho de que, dada una ejecución del modelo, algún resultado debe ocurrir). En el ejemplo anterior, la probabilidad del conjunto de resultados ${\displaystyle P({\text{Cabeza}},{\text{Cola}})}$ debe ser igual a uno, porque es totalmente seguro que el resultado será ${\displaystyle {\text{Cabeza}}}$ o ${\displaystyle {\text{Cola}}}$ (el modelo ignora cualquier otra posibilidad) en un solo lanzamiento de moneda.

No todos los subconjuntos del espacio muestral ${\displaystyle \Omega }$ deben ser considerados necesariamente como un evento: algunos de los subconjuntos simplemente no son de interés, otros no pueden ser "medido". Esto no es tan evidente en un caso como el lanzamiento de una moneda. En un ejemplo diferente, se podrían considerar las longitudes de los lanzamientos de jabalina, donde los eventos son típicamente intervalos como "entre 60 y 65 metros" y uniones de tales intervalos, pero no conjuntos como los "números irracionales entre 60 y 65 metros".

Un espacio de probabilidad es la terna ${\displaystyle (\Omega ,{\mathcal {F}},\operatorname {P} )}$ donde el conjunto ${\displaystyle \Omega }$ es llamado espacio muestral y es el conjunto de los posibles resultados del experimento, ${\displaystyle {\mathcal {F}}}$ es una σ-álgebra de subconjuntos de ${\displaystyle \Omega }$ que satisface

1. ${\displaystyle \Omega \in {\mathcal {F}}}$.
2. Si ${\displaystyle A\in {\mathcal {F}}}$ entonces ${\displaystyle A^{c}\in {\mathcal {F}}}$.
3. Si ${\displaystyle A_{1},A_{2},\dots ,A_{n}\in {\mathcal {F}}}$ entonces ${\displaystyle A_{1}\cup A_{2}\cup \cdots \cup A_{n}\in {\mathcal {F}}}$.

Al par ${\displaystyle (\Omega ,{\mathcal {F}})}$ se le conoce como un espacio de medida. Por último, ${\displaystyle \operatorname {P}$ :{\mathcal {F}}\to [0,1]} es una función conocida como medida de probabilidad o función de probabilidad que asigna una probabilidad a todo suceso y que verifica los llamados axiomas de Kolmogorov:

1. ${\displaystyle \operatorname {P} (\Omega )=1}$.
2. ${\displaystyle \operatorname {P} (A)\geq 0}$, ${\displaystyle \forall \;A\in {\mathcal {F}}}$.
3. Si ${\displaystyle A_{1},A_{2},\dots ,A_{n}\in {\mathcal {F}}}$ y ${\displaystyle A_{i}\cap A_{j}=\emptyset }$ para ${\displaystyle i\neq j}$ entonces

${\displaystyle {\begin{aligned}\operatorname {P} \left(\bigcup _{i=1}^{n}A_{i}\right)&=\sum _{i=1}^{n}\operatorname {P} [A_{i}]\\&=\operatorname {P} [A_{1}]+\operatorname {P} [A_{2}]+\cdots +\operatorname {P} [A_{n}]\end{aligned}}}$

La Teoría de la probabilidad discreta sólo necesita espacios muestrales ${\displaystyle \Omega }$ de a lo sumo contable. Se pueden atribuir probabilidades a puntos de ${\displaystyle \Omega }$ mediante la función de masa de probabilidad ${\displaystyle p:\Omega \to [0,1]}$ tal que ${\textstyle suma_{\omega \in \Omega }p(\omega )=1}$. Todos los subconjuntos de ${\displaystyle \Omega }$ pueden tratarse como sucesos (así, ${\displaystyle {\mathcal {F}}=2^{\Omega }}$ es el conjunto potencia). La medida de probabilidad toma la forma simple

$${\displaystyle P(A)=\sum _{\omega \in A}p(\omega )\quad {\text{for all }}A\subseteq \Omega .}$$

(⁎)

La mayor σ-álgebra ${\displaystyle {\mathcal {F}}=2^{\Omega }}$ describe la información completa. En general, una σ-álgebra ${\displaystyle {\mathcal {F}}\subseteq 2^{\Omega }}$ corresponde a una partición finita o contable. ${\displaystyle \Omega =B_{1}\cup B_{2}\cup \dots }$, siendo la forma general de un suceso ${\displaystyle A\in {\mathcal {F}}}$ ${\displaystyle A=B_{k_{1}}cupB_{k_{2}}cup\dots }$. Véanse también los ejemplos.

El caso ${\displaystyle p(\omega )=0}$ está permitido por la definición, pero rara vez se utiliza, ya que tal ${\displaystyle \omega }$ puede excluirse con seguridad del espacio muestral.

Si Ω es incontable, aun así, puede ocurrir que p(ω) ≠ 0 para algún ω; tales ω se llaman átomos. Son un conjunto a lo sumo contable (tal vez vacío), cuya probabilidad es la suma de las probabilidades de todos los átomos. Si esta suma es igual a 1, todos los demás puntos pueden excluirse con seguridad del espacio muestral, lo que nos devuelve al caso discreto. En caso contrario, si la suma de probabilidades de todos los átomos está entre 0 y 1, entonces el espacio de probabilidad se descompone en una parte discreta (atómica) (tal vez vacía) y una parte no atómica.

Si p(ω) = 0 para todo ω ∈ Ω (en este caso, Ω debe ser incontable, porque si no P(Ω) = 1 no podría satisfacerse), entonces la ecuación (⁎) falla: la probabilidad de un conjunto no es necesariamente la suma sobre las probabilidades de sus elementos, ya que la suma sólo está definida para números contables de elementos. Esto hace que la teoría del espacio de probabilidad sea mucho más técnica. Se aplica una formulación más fuerte que la suma, la teoría de la medida. Inicialmente, las probabilidades se atribuyen a algunos conjuntos "generadores" (véanse los ejemplos). A continuación, un procedimiento de limitación permite asignar probabilidades a conjuntos que son límites de secuencias de conjuntos generadores, o límites de límites, y así sucesivamente. Todos estos conjuntos son la σ-álgebra ${\displaystyle {\mathcal {F}}}$. Los conjuntos pertenecientes a ${\displaystyle {\mathcal {F}}}$ se llaman medibles. En general son mucho más complicados que los conjuntos generadores, pero mucho mejores que los conjuntos no medibles.

Un espacio de probabilidad ${\displaystyle (\Omega ,\;{\mathcal {F}},\;P)}$ se dice que es un espacio de probabilidad completo si para todo ${\displaystyle B\in {\mathcal {F}}}$ con ${\displaystyle P(B)=0}$ y todo ${\displaystyle A\;\subset \;B}$ se tiene ${\displaystyle A\in {\mathcal {F}}}$. A menudo, el estudio de los espacios de probabilidad se restringe a espacios de probabilidad completos.

• Variable aleatoria
• Proceso estocástico

• Sazonov, V.V. (2001), «Probability space», en Hazewinkel, Michiel, ed., Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
• Animation demonstrating probability space of dice
• Virtual Laboratories in Probability and Statistics (principal author Kyle Siegrist), especially, Probability Spaces
• Citizendium
• Complete probability space
• Weisstein, Eric W. «Espacio de probabilidad». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.