Estructura algebraica
En álgebra abstracta, una estructura algebraica, también conocida como sistema algebraico,[1] es una n-tupla (a1, a2, ..., an), donde a1 es un conjunto dado no vacío, y {a2, ..., an} un conjunto de operaciones aplicables a los elementos de dicho conjunto.
Aquí se definen las estructuras algebraicas más conocidas según la operación de suma y multiplicación
Principales estructuras algebraicas
Las estructuras algebraicas se clasifican según las propiedades que cumplen las operaciones sobre el conjunto dado. En estructuras algebraicas más elaboradas, se definen además varias leyes de composición.
Con una ley de composición interna
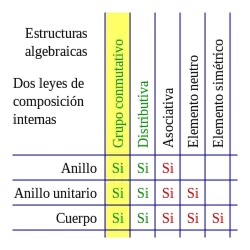
Con dos leyes de composición interna
- Semianillo
- Anillo
- Pseudoanillo
- Dominio de integridad
- Cuerpo
- Retículo (orden)
- Álgebra de Boole
- Álgebra de Heyting
Con leyes de composición interna y externa
Referencias
- Sigler, L.E. (1981), Álgebra (1ª. edición), Barcelona: Editorial Reverté, p. 476, ISBN 9788429151299.
Bibliografía
- Adler, Irving (1970). La Nueva Matemática. Buenos Aires: Editorial Universitaria de Buenos Aires, Colección Ciencia Joven, 288 páginas, en rústica. Traducción del inglés: Jorge Jáuregui. Original: The New Mathematics, The John Day Company, New York. ISBN 0-381-98002-2.
- Birkhoff, Garrett; MacLane, Saunders (1963). Álgebra Moderna. Barcelona: Vicens-Vives. ISBN 978-0828403306.
- Kurosch, A. G. (1981). Álgebra superior (4 edición). Moscú: Mir. ISBN 9681849388.
Enlaces externos
Wikilibros alberga un libro o manual sobre Álgebra Abstracta. incluyendo un capítulo sobre Estructuras Algebraicas.
| Control de autoridades |
|
|---|
Datos: Q205464
Multimedia: Algebraic structures / Q205464
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.