Eudoxo de Cnido
Eudoxo de Cnido (en griego Εὔδοξος ὁ Κνίδιος [Eúdoxos ho Knídios]; Cnido, actual Turquía, c. 390 a. C.-c. 337 a. C.) fue un filósofo, astrónomo, matemático y médico de la Antigua Grecia, pupilo de Platón. Nada de su obra ha llegado a nuestros días; todas las referencias con las que contamos provienen de fuentes secundarias, como el poema de Arato sobre astronomía.
| Eudoxo de Cnido | ||
|---|---|---|
| Información personal | ||
| Nombre en griego antiguo | Εὔδοξος ὁ Κνίδιος | |
| Nacimiento |
408 a. C. o años 390 a. C. Cnido (Antigua Grecia) | |
| Fallecimiento |
355 a. C. Cnido (Antigua Grecia) | |
| Educación | ||
| Alumno de | ||
| Información profesional | ||
| Ocupación | Matemático, escritor, filósofo y geógrafo | |
| Área | Matemáticas y astronomía | |
| Alumnos | Menecmo, Dinóstrato y Calipo de Cícico | |
Eudoxo fue el primero en plantear un modelo planetario basado en un modelo matemático, por lo que se le considera el padre de la astronomía matemática.[1]
Biografía
Eudoxo nació en Cnido, quizás en el año 408 a. C., aunque otros autores lo trasladan 8 años hasta 400 a. C. o 18 hasta 390 a. C. Probablemente nació en una familia relacionada con la medicina, ya que esos fueron sus primeros estudios, bajo la tutela de Filisto, y ejerció la profesión durante algunos años.[2] Aprendió también matemáticas de Arquitas. En Atenas acudió a la Academia de Platón y posteriormente, recomendado por el rey Agesilao II al faraón Nectanebo I, estudió astronomía en Heliópolis durante más de un año.[3]
A su vuelta, fundó en Cícico una escuela de filosofía, matemáticas y astronomía; también enseñó en otras ciudades del Asia Menor. De nuevo en Atenas, sobre el año 368 a. C., volvió a tomar contacto con Platón y figuró como uno de los miembros más brillantes de la Academia. Su relación con Platón es uno de los puntos más comentados de su biografía y la naturaleza de dicha relación no es clara: según Diógenes Laercio, Platón lo recibió hostilmente, celoso de su popularidad; Plutarco afirma que desconfiaba de las ideas matemáticas de Eudoxo. Otras fuentes, no obstante, afirman que la relación fue cordial y Eudoxo siguió las orientaciones de Platón.[3] Alrededor del año 350 a. C., Eudoxo retornó a Cnido, donde acababa de instaurarse un régimen democrático y se le encargó redactar la nueva constitución.[2]
Filóstrato lo incluye en el Libro I de su obra Vidas de los Sofistas en razón del ornato de su lenguaje y su facilidad para la improvisación. Eudoxo murió en su ciudad natal en el año 355 a. C. (en el 347 a. C. si consideramos el nacimiento en el 400 a. C., en 337 a. C. si lo consideramos en 390 a. C.).
Astronomía

Su fama en astronomía matemática se debe a la invención de la esfera celeste y a sus precoces aportaciones para comprender el movimiento de los planetas, que recreó construyendo un modelo de esferas homocéntricas que representaban las estrellas fijas, la Tierra, los planetas conocidos, el Sol y la Luna, y dividió la esfera celeste en grados de latitud y longitud.
Su modelo cosmológico afirmaba que la Tierra era el centro del universo y el resto de cuerpos celestes la rodeaban fijados a un total de veintisiete esferas[4] reunidas en siete grupos. En este modelo se basó Aristóteles para desarrollar su propio modelo cosmológico.[5] Hay referencias a explicaciones suyas cíclicas de los fenómenos naturales de la Tierra, en Plinio el Viejo.[6]
Para explicar las retrogradaciones que se observaban en el movimiento de los planetas (aparentemente, vistos desde la Tierra, retroceden en su órbita), Eudoxo introdujo la hipopede o lemniscata esférica, que es resultado de la combinación del movimiento de las dos esferas más internas de su modelo. Sobre esta figura rotaría cada cuerpo celeste en correspondencia con su período sinódico. Por su parte, el tiempo de rotación sobre la esfera en que se encuentra corresponde a su periodo sideral.[7]
Modelos planetarios eudoxánicos
Una idea general del contenido de Sobre las velocidades puede extraerse de la Metafísica XII, 8 de Aristóteles, y de un comentario de Simplicio de Cilicia (siglo VI d. C.) sobre De caelo, otra obra de Aristóteles. Según un relato de Simplicio, Platón planteó una pregunta a los astrónomos griegos: "¿Qué movimientos uniformes y ordenados pueden explicar los movimientos aparentes de los planetas?"[8] Platón propuso que los movimientos errantes aparentemente caóticos de los planetas podían explicarse mediante combinaciones de movimientos circulares uniformes centrados en una Tierra esférica, una idea aparentemente novedosa en el siglo IV a. C.
En la mayoría de las reconstrucciones modernas del modelo eudoxiano, a la Luna se le asignan tres esferas:
- La más externa gira hacia el oeste una vez cada 24 horas, explicando la salida y la puesta.
- La segunda gira hacia el este una vez al mes, explicando el movimiento mensual de la Luna a través del zodíaco.
- La tercera también completa su revolución en un mes, pero su eje está inclinado en un ángulo ligeramente diferente, lo que explica el movimiento en latitud (desviación de la eclíptica) y el movimiento de los nodos lunares.
Al Sol también se le asignan tres esferas. La segunda completa su movimiento en un año en lugar de un mes. La inclusión de una tercera esfera implica que Eudoxo creía erróneamente que el Sol tenía movimiento en latitud.
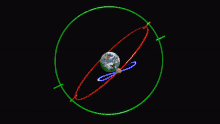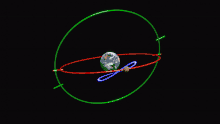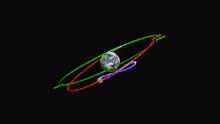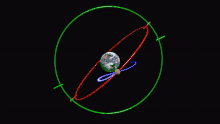
[File:Eudoxus' Homocentric Spheres.png|thumb|Modelo de movimiento planetario de Eudoxo. Cada una de sus esferas homocéntricas se representa aquí como un anillo que gira sobre el eje indicado. La esfera más externa (amarilla) gira una vez al día; la segunda (azul) describe el movimiento del planeta a través del zodíaco; la tercera (verde) y la cuarta (roja) juntas mueven el planeta a lo largo de una curva en forma de ocho (o hipopótamo) para explicar el movimiento retrógrado.
A los cinco planetas visibles (Mercurio, Venus, Marte, Júpiter y Saturno) se les asignan cuatro esferas a cada uno:
- La más externa explica el movimiento diario.
- La segunda explica el movimiento del planeta a través del zodíaco.
- La tercera y la cuarta explican conjuntamente el retrogradación, cuando un planeta parece ralentizarse y luego invierte brevemente su movimiento a través del zodíaco. Inclinando los ejes de las dos esferas entre sí y haciéndolas girar en direcciones opuestas pero con periodos iguales, Eudoxo podía hacer que un punto de la esfera interior trazara una forma de ocho, o hipopótamo.
Matemáticas
Eudoxo es considerado por algunos como el más grande de matemático griego clásico, y en toda la Antigüedad sólo es superado por Arquímedes.[9] Eudoxo fue probablemente la fuente de la mayor parte del libro V de Elementos de Euclides.[10] Desarrolló con rigor el método de agotamiento de Antifón, precursor del cálculo integral que también utilizó de forma magistral Arquímedes en el siglo siguiente. Aplicando el método, Eudoxo demostró afirmaciones matemáticas tales como: las áreas de los círculos son entre sí como los cuadrados de sus radios, los volúmenes de las esferas son entre sí como los cubos de sus radios, el volumen de una pirámide es un tercio del volumen de un prisma con la misma base y altitud, y el volumen de un cono es un tercio del del cilindro correspondiente.[11]
Eudoxo introdujo la idea de magnitud matemática no cuantificada para describir y trabajar con entidades geométricas continuas como líneas, ángulos, áreas y volúmenes, evitando así el uso de números irracionales. Al hacerlo, invirtió el énfasis del pitagorismo en el número y la aritmética, centrándose en cambio en los conceptos geométricos como base de unas matemáticas rigurosas. Algunos pitagóricos, como el maestro de Eudoxo Arquitas, habían creído que sólo la aritmética podía proporcionar una base para las pruebas. Inducido por la necesidad de comprender y operar con cantidades inconmensurables, Eudoxo estableció lo que puede haber sido la primera organización deductiva de las matemáticas sobre la base de axiomass explícitos. El cambio de enfoque de Eudoxo estimuló una división en las matemáticas que duró dos mil años. En combinación con una actitud intelectual griega despreocupada por los problemas prácticos, se produjo un importante retroceso en el desarrollo de las técnicas de la aritmética y el álgebra.[11]
Fue discípulo de Arquitas de Tarento. Su trabajo sobre la teoría de la proporcionalidad denota una amplia comprensión de los números y permite el tratamiento de las cantidades continuas, no únicamente de los números enteros o números racionales. Cuando en esta teoría fue resucitada por Tartaglia y otros estudiosos en el siglo XVI, se convirtió en la base de cuantitativas obras de ciencias durante un siglo, hasta que fue sustituida por los métodos algebraicos de Descartes. A él se debe el método de exhausción - que puede ser considerado el logro más destacado de la matemática antigua- y, además, la teoría general de las magnitudes geométricas.[12]
Eudoxo demostró que el volumen de una pirámide es la tercera parte del de un prisma de su misma base y altura; y que el volumen de un cono es la tercera parte del de un cilindro de su misma base y altura, teoremas ya intuidos por Demócrito.[7] Para demostrarlo elaboró el llamado método exhaustivo,[13] antecedente del cálculo integral,[2] para calcular áreas y volúmenes. El método fue utilizado magistralmente por Arquímedes. El trabajo de ambos como precursores del cálculo fue únicamente superado en sofisticación y rigor matemático por Newton y Leibniz.
Una curva algebraica lleva su nombre, la campila de Eudoxo:
Ética
Aristóteles, en la Ética a Nicómaco, atribuye a Eudoxo los siguientes argumentos a favor del hedonismo:
- Todas las cosas, racionales e irracionales, apuntan al placer.
- Las cosas apuntan a lo que creen que es bueno; una buena indicación de lo que es el bien principal sería la cosa a la que apunta la mayoría de las cosas.
- De manera similar, el placer opuesto, el dolor, se evita universalmente, lo que proporciona un apoyo adicional a la idea de que el placer se considera universalmente bueno.
- La gente no busca el placer como un medio para otra cosa, sino como un fin en sí mismo.
- Cualquier otro bien que se pueda imaginar sería mejor si se le añadiera placer, y solo mediante el bien se puede aumentar el bien.
- De todas las cosas que son buenas, la felicidad es peculiar por no ser elogiada, lo que puede mostrar que es el bien supremo.
«Estas razones de Eudoxo más persuadían por la bondad de las costumbres del hombre, que por sí mismas, porque por extremo se mostraba ser templado en su vivir. De manera que no parecería que decía esto como hombre al deleite aficionado, sino que, en realidad de verdad, era ello así como él decía.»Ética a Nicómaco, Libro X, Capítulo 2, 1172b 9
Reconocimientos
- El cráter lunar Eudoxus lleva este nombre en su memoria.
- El cráter marciano Eudoxus también conmemora su nombre.
Véase también
Referencias
- Centro Virtual de Divulgación de las Matemáticas, página desarrollada por la Comisión de Divulgación de la Real Sociedad Matemática Española.
- Eudoxo de Cnido y las esferas en Astromía.com
- Eudoxo de Cnido, p. 2/3 Archivado el 26 de noviembre de 2011 en Wayback Machine.. Centro Virtual de Divulgación de las Matemáticas, página desarrollada por la Comisión de Divulgación de la Real Sociedad Matemática Española.
- Eudoxio de Cnido La astronomía helénica, en la Web de la Asociación Larense de Astronomía.
- Aristóteles: Filosofía y Tierra redonda en Astromía.com
- Plinio el Viejo - Historia Naturalis Libro II, 130.
- Eudoxo de Cnido, p. 3/3 Archivado el 26 de noviembre de 2011 en Wayback Machine.. Centro Virtual de Divulgación de las Matemáticas, página desarrollada por la Comisión de Divulgación de la Real Sociedad Matemática Española.
- Lloyd, GER (1970). Early Greek Science: Thales to Aristotle. W.W. Norton. p. 84. ISBN 9780393005837. (requiere registro).
- Calinger, Ronald (1982). Clásicos de Matemáticas. Oak Park, Illinois: Moore Publishing Company, Inc. p. 75. ISBN 0-935610-13-8.
- Ball, 1908, p. 54.
- Morris Kline, Mathematical Thought from Ancient to Modern Times Oxford University Press, 1972 pp. 48-50
- I.M. Yaglom. La matemática en el mundo real ISBN 978-5-396-00062-9 distribuido por Hayka libros desde Sevilla, España
- Ruiz, Ángel. Eudoxo. Geometrías no eucladianas. Capítulo I: una introducción. En la Antigüedad griega
Bibliografía
- Ball, Walter William Rouse (1908). A Short Account of the History of Mathematics (4th edición). Dover Publications. ISBN 9780486206301.
- De Santillana, G. (1968). «Eudoxus and Plato: A Study in Chronology». Reflections on Men and Ideas. Cambridge, MA: MIT Press.
- Evans, James (1998). The History and Practice of Ancient Astronomy. Oxford University Press. ISBN 0-19-509539-1. OCLC 185509676.
- Huxley, GL (1980). Eudoxus of Cnidus p. 465-7 in: the Dictionary of Scientific Biography, volume 4.
- Huxley, G. L. (1963). «Eudoxian Topics». Greek, Roman, and Byzantine Studies 4: 83-96.
- Knorr, Wilbur Richard (1978). «Archimedes and the Pre-Euclidean Proportion Theory». Archives Internationales d'Histoire des Sciences 28: 183-244.
- Knorr, Wilbur R. (1986). The Ancient tradition of geometric problems. Boston: Birkhäuser. ISBN 0-8176-3148-8.
- Lasserre, François (1966) Die Fragmente des Eudoxos von Knidos (de Gruyter: Berlin)
- Plantilla:Cite LotEP
- Manitius, C. (1894) Hipparchi in Arati et Eudoxi Phaenomena Commentariorum Libri Tres (Teubner)
- Neugebauer, O. (1975). A history of ancient mathematical astronomy. Berlin: Springer-Verlag. ISBN 0-387-06995-X.
- Van der Waerden, B. L. (1988). Science Awakening (5th edición). Leiden: Noordhoff.
Enlaces externos
- Diógenes Laercio: Vidas, opiniones y sentencias de los filósofos más ilustres; VIII, 86 - 91: Eudoxo.
- Leptine: Didascalia celeste o El arte de Eudoxo.