Serie de Laurent
En matemáticas, la serie de Laurent de una función compleja es la representación de la misma función en la forma de una serie de potencias, la cual también incluye términos de grado negativo. Esta serie se puede usar para expresar funciones complejas en casos donde una expansión de la serie de Taylor no es aplicable o no se puede acoplar. La serie de Laurent fue descubierta por Karl Weierstrass en el año de 1841, pero no lo publicó en ese entonces,[1] paralelamente, el matemático francés Pierre Alphonse Laurent desarrolló las series, y fue quien la publicó por primera vez en el año 1843.[2]
Definición
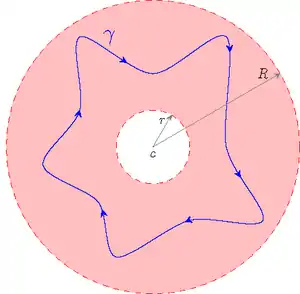
Una serie de Laurent se define con respecto a un punto particular y un camino de integración . El camino de integración debe estar dentro de una región donde es una función holomorfa (a veces se usa como sinónimo el término función analítica, aunque no es estrictamente correcto, dado que una función analítica es técnicamente aquella que admite desarrollo en serie de potencias en cierto entorno de un punto, lo que ocurre es que en toda función holomorfa es también analítica).
Una serie de Laurent centrada alrededor de un punto es una serie de la forma:
donde . Los coeficientes de una serie de Laurent en una función analítica se pueden encontrar por medio de la fórmula integral de Cauchy y están dados por:
para . La sucesión de constantes están definidas por un camino de integración en la generalización de la fórmula integral de Cauchy.
Convergencia
Podemos demostrar que esta serie es convergente dentro del conjunto (posiblemente vacío):
Donde:
- y
Toda serie de Laurent tiene vinculada una función de la forma:
cuyo dominio es el conjunto de puntos en sobre el cual es convergente. Esta función es analítica dentro de una corona ; inversamente, toda función en una corona es igual a una única serie de Laurent.
Si suponemos : es una serie de Laurent con coeficientes an y un centro complejo c. Entonces existe un radio interior r y un radio exterior R de tal forma que:
- La serie de Laurent es convergente en la corona abierta , tanto para potencias de grado positivo como para potencias de grado negativo y esta convergencia define una función holomorfa en la corona abierta.
- Fuera de la corona, la serie de Laurent es divergente.
- Para el disco existe al menos un punto en la frontera interior y otro en la frontera exterior para los cuales no puede ser holomorfa continua.
Singularidades
La serie de Laurent es muy importante en el análisis complejo, especialmente para investigar el comportamiento de funciones cerca de singularidades, pues permite saber qué tipos de singularidades tiene una función. Así, si expandimos una función en serie de Laurent, tomando como centro una singularidad y como radio interior cero, la cantidad de potencias negativas en la serie indicará que tipo de singularidad es:
- Si la serie no tiene potencias negativas, la singularidad es evitable
- Si la serie tiene finitas potencias negativas, la singularidad es un polo
- Si la serie tiene infinitas potencias negativas, la singularidad es una singularidad esencial
Véase también
Referencias
- O'Connor, John J.; Robertson, Edmund F. (2004), «Serie de Laurent» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Laurent_Pierre.html.
- Nahim, Paul J. (2008). Esto no es real. La historia de i. Libraria. p. 234. ISBN 9685374244. «Epílogo: que viene después ».
Bibliografía
- Marsden, Jerrold E.; Hoffmann, Michael J. (2012). Análisis básico de variable compleja (Obdulia Mendoza Hernández y Gustavo Izquierdo Buenrostro, trads.). México, D.F.: Trillas. ISBN 9789682452031. OCLC 914504275.
- Cartan, Henri (1995). Elementary Theory of Analytic Functions of One or Several Complex Variables (en inglés). Nueva York: Dover Publications. ISBN 0486685438. OCLC 797633389. Resumen divulgativo.
- Robert E. Greene, Steven G. Krantz (2006). Function Theory of One Complex Variable. Graduate Studies in Mathematics (en inglés) 40 (3ª edición). AMS. ISBN 978-0-8218-3962-1.
- David C. Ullrich (2008). Complex Made Simple. Graduate Studies in Mathematics (en inglés) 97. AMS. ISBN 978-0-8218-4479-3.
Enlaces externos
- Weisstein, Eric W. «Laurent Series». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.