Experimento de Davisson-Germer

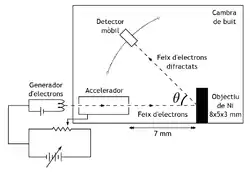
El aparato empleado por Davisson y Germer constaba de un cañón de electrones que se generaban por efecto termoiónico en una cinta de tungsteno calentada por el efecto Joule. Una vez emitidos, los electrones pasaban a una pequeña cámara donde estaban acelerados mediante una diferencia de potencial de decenas de voltios (entre 15 V y 350 V). El haz acelerado, de 1 mm de diámetro, se dirigía hacia un monocristal de níquel situado a 7 mm de la salida de los electrones, que impactaban verticalmente. El objetivo era un monocristal de níquel de 8 mm × 5 mm × 3 mm, que podía girar sobre el eje de incidencia del haz de electrones. El níquel tiene una estructura cristalina de tipo cúbica centrada en la cara. La cara que recibía el haz de electrones de forma perpendicular era paralela al plano cristalográfico definido por la índice de Miller (111).

Los electrones eran difractados por níquel y salían con un cierto ángulo que podía ser determinado mediante un detector, constituido por una doble jaula de Faraday y un galvanómetro que podía rotar entre 20 ° y 90 ° respecto de la dirección del haz incidente, al tiempo que medía la intensidad del haz de electrones. Ambos haces se movían en una cámara donde se había hecho el vacío a una presión entre 2·10^-6 mm Hg i 3·10^-6 mm Hg.[5]

Intensidad de los electrones difractados para un voltaje de 54 V y lanzados perpendicularmente contra el plan cristalográfico (111) respecto del ángulo de difracción (coordenadas polares).

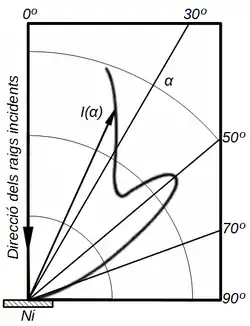
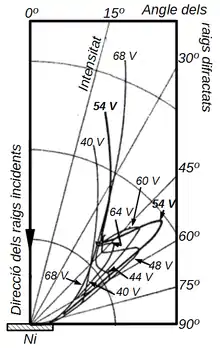
Davisson y Germer observaron que cuando hacían incidir los electrones acelerados sobre la superficie de níquel se producían máximos de intensidad que no se podían explicar considerando el electrón como una partícula que choca contra una superficie llena de átomos de níquel esféricos, los cuales deberían de dispersar los electrones en todas direcciones. La máxima intensidad se alcanzaba acelerando los electrones con una diferencia de potencial de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \triangle V=54 V} contra el cristal de níquel orientado con capas de átomos perpendiculares a la dirección de incidencia. En este caso concreto se producía una difracción por reflexión de los electrones con un máximo de intensidad a ${\displaystyle \alpha =50^{\circ }}$ de la dirección de incidencia.[16]

Esquema de la difracción de electrones en la superficie de un cristal de Ni

Sin embargo el fenómeno observado era similar a la difracción de rayos X sobre una superficie cristalina descubierta en 1912 por el físico alemán Max von Laue con sus colaboradores Paul Knipping y Walter Friedrich, lo que le permitió determinar la naturaleza ondulatoria de los rayos X, considerados hasta ese momento como haces de partículas de alta energía. La difracción de los rayos X fue estudiada en 1913 por William Lawrence Bragg y William Henry Bragg, los cuales pudieran relacionar los máximos de intensidad con las distancias entre las capas de átomos de un cristal.

La difracción de rayos X se produce porque esta radiación electromagnética tiene longitudes de onda muy corta, entre 10 nm y 100 pm, comparables a las distancias interatómicas los cristales (en el níquel esta es ${\displaystyle D=215\;pm}$).En este caso se produce una dispersión de una manera especular, por reflexión, por los átomos del cristal, y los diferentes rayos difractados interfieren con interferencias constructivas y destructivas. Las primeras refuerzan la intensidad del haz y las segundas lo anulan.[16]

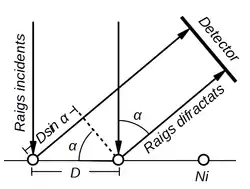
En el experimento de Davisson y Germer se recogen los datos de la interferencia constructiva. La condición de interferencia constructiva para átomos adyacentes, la que produce un máximo de intensidad, es aquella que cumple que la diferencia de caminos, esto es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle D \cdot \sin \, \alpha} , de dos rayos difractados es igual a la longitud de onda, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \lambda , cuando se difractan rayos X. Aplicando la misma condición se puede calcular la longitud de onda de los electrones difractados:[16]

${\displaystyle \lambda =D\cdot \sin \alpha =215\,pm\cdot \sin 50^{\circ }=215\,pm\,\cdot 0,766=165\,pm}$

Louis-Victor-Pierre-Raymond de Broglie (1892-1987)

La fórmula que dio De Broglie para la longitud de onda de una partícula de masa ${\displaystyle m}$ que se mueve a una velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): v és:[3]

${\displaystyle \lambda ={\frac {h}{mv}}}$

donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): h es la constante de Planck que vale Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle 6,626 \cdot 10^{-34} J \cdot s} .

La velocitad ${\displaystyle v}$ de un electrón de carga ${\displaystyle e}$ y masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): m ,acelerado por una diferencia de potencialError al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \triangle V} se puede deducir con velocidades reducidas, es decir, sin considerar efectos relativistas, a partir de igualar el trabajo eléctrico${\displaystyle W_{AB}=-e\cdot \triangle V}$ y la variación de energía cinética entre el inicio y el final, ${\displaystyle \triangle K_{AB}=K_{B}-K_{A}}$. Como los electrones se aceleran desde el reposo esError al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle v_A = 0} y tenemos:

Igualando esta expresión en el trabajo eléctrico queda:

${\displaystyle {\tfrac {1}{2}}mv_{B}^{2}=-e\cdot \triangle V}$

Como la carga del electrón es negativa podemos escribir finalmente que:

${\displaystyle v_{B}={\sqrt {\frac {2e\triangle V}{m}}}}$

La longitud de onda de De Broglie será:

${\displaystyle \lambda ={\frac {h}{\sqrt {2me\triangle V}}}}$

Si se sustituye por los valores${\displaystyle h=6,626\cdot 10^{-34}J\cdot s}$; Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle m=9,1 \cdot 10^{-31} kg} ; Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle e=1,602 \cdot 10^{-19} C} ; i ${\displaystyle \triangle V=54V}$;

queda:

Este valor coincide, dentro de los márgenes experimentales, con el valor obtenido por Davisson y Germer, lo que confirma la hipótesis de De Broglie. Como también lo confirman los datos obtenidos con experimentos con otros voltajes y con haces de electrones que incidían sobre superficies diferentes del cristal.

La difracción de los electrones, de la misma manera que los rayos X, se produce en ciertas direcciones preferentes que implican la participación de varias capas de planos paralelos de átomos de níquel dentro del cristal, ya que por su pequeña longitud de onda los rayos X tienen la capacidad de penetrar. Se cumple la fórmula de Bragg:

Esquema de la difracción de electrones en el experimento de Davisson-Germer. El haz incidente impacto perpendicularmente a la superficie del Ni y llega a un plano cristalográfico con un ángulo ${\displaystyle \alpha /2}$ respecto de la normal (línea discontinua) y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \theta respecto del plano. El haz reflejado también lo hace con un ángulo igual Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \alpha /2} respecto de la normal y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \theta respecto del plano. El ángulo medido es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): \alpha .

con:

• Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): d = distancia entre dos planos cristalográficos;
• ${\displaystyle \theta }$ =ángulo de difracción, ángulo entre el haz incidente y la dirección cristalográfica o el plan del cristal que produce la difracción;
• ${\displaystyle n}$ = orden de difracción (1, 2, 3,...);
• ${\displaystyle \lambda }$ = longitud de onda de los electrones.

En la experiencia de Davisson y Germer sobre un monocristal de níquel el haz de electrones penetran dentro del cristal y se reflejan en diferentes planos paralelos separados una distancia ${\displaystyle d=91\,pm}$ y con un ángulo de difracción Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \theta = 65^\circ} . Aplicando la fórmula de Bragg al máximo de primer orden Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): n=1 resulta:

${\displaystyle \lambda =2\cdot d\cdot \sin \theta =2\cdot 0,91\,pm\cdot \sin 65^{\circ }=165\,pm}$[17]

Se puede relacionar la distancia interatómica en la superficie del cristal, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): D , con la separación entre planos cristalográficos, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): d , y el ángulo ${\displaystyle \alpha }$ entre el haz de rayos incidentes y el haz de rayos difractados. La mitad de este ángulo es igual al ángulo que forma la superficie del cristal y la dirección de los planos cristalográficos, ya que la reflexión del haz de electrones cumple la ley de la reflexión (rayo incidente y rayo reflejado forman el mismo ángulo con la normal a la superficie de reflexión). Así pues, el ángulo entre el haz incidente y la normal es ${\displaystyle \alpha /2}$, y estas dos direcciones son perpendiculares a la superficie del cristal y el plano cristalográfico respectivamente, por lo tanto éstas forman el mismo ángulo ${\displaystyle \alpha /2}$. La relación resulta ser:

El ángulo entre el haz incidente y el plano cristalográfico, ${\displaystyle \theta }$, es igual a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \tfrac{\pi}{2} - \tfrac{\alpha}{2} } . Y la fórmula de Bragg se puede poner en función de este nuevo ángulo${\displaystyle \alpha /2}$ y simplificar usando la identidad trigonométrica ${\displaystyle \sin \left({\tfrac {\pi }{2}}-\beta \right)=\cos \beta }$:

${\displaystyle 2\cdot d\cdot \sin \,\theta =2\cdot d\cdot \sin \left({\tfrac {\pi }{2}}-{\tfrac {\alpha }{2}}\right)=2\cdot d\cdot \cos {\tfrac {\alpha }{2}}=n\cdot \lambda }$

Si se sustituye ${\displaystyle d}$:

${\displaystyle 2\cdot D\cdot \sin {\tfrac {\alpha }{2}}\cdot \cos {\tfrac {\alpha }{2}}=n\cdot \lambda }$

o, empleando la identidad trigonométrica del ángulo doble ${\displaystyle 2\cdot \sin \beta \cdot \cos \beta =\sin 2\beta }$:

${\displaystyle D\cdot \sin \alpha =n\cdot \lambda }$

que es la ecuación empleada para demostración en el caso de reflexión en la superficie.[16]