Difracción

Aproximación numérica del patrón de difracción de una ranura de ancho de cuatro longitudes de onda con una onda plana incidente. El haz central principal, los valores nulos y las inversiones de fase son evidentes.

Gráfico e imagen de difracción en una sola rendija.

Una rendija larga de ancho infinitesimal que está iluminada por luz, la difracta en una serie de ondas circulares y el frente de onda que emerge de la hendidura es una onda cilíndrica de intensidad uniforme, acorde con el principio de Huygens-Fresnel.

Una ranura que es más amplia que la longitud de onda produce efectos de interferencia en el espacio descendente de la ranura. Esto puede explicarse suponiendo que la hendidura se comporta como si tuviera una gran cantidad de fuentes puntuales espaciadas uniformemente a lo ancho de la hendidura. El análisis de este sistema se simplifica si consideramos la luz de una sola longitud de onda. Si la luz incidente es coherente, todas estas fuentes pasan a tener la misma fase. La luz en un punto dado en el espacio descendente de la rendija se compone de contribuciones de cada una de estas fuentes puntuales y si las fases relativas de estas contribuciones varían en 2π o más, podemos esperar a encontrar mínimos y máximos en la luz difractada. Dichas desfases son causadas por diferencias en las longitudes de trayectoria sobre las cuales los rayos contribuyentes alcanzan el punto desde la ranura.

Podemos encontrar el ángulo en el que se obtendrá un primer mínimo en la luz difractada mediante el siguiente razonamiento. La luz de una fuente ubicada en el borde superior de la rendija interfiere destructivamente con una fuente ubicada en el medio de la rendija, cuando la diferencia de trayectoria entre ellas es igual a λ / 2. Similarmente, la fuente justo debajo de la parte superior de la ranura interferirá destructivamente con la fuente ubicada justo debajo de la mitad de la ranura en el mismo ángulo. Podemos continuar este razonamiento a lo largo de toda la altura de la hendidura para concluir que la condición de interferencia destructiva para toda la hendidura es la misma que la condición de interferencia destructiva entre dos hendiduras estrechas a una distancia de la mitad del ancho de la hendidura. La diferencia de trayectoria es aproximadamente Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \frac{d \sin(\theta)}{2}} para que la intensidad mínima ocurra en un ángulo θ _min definido por:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle d\,\sin\theta_\text{min} = \lambda}

donde:

• d es el ancho de la ranura,
• Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \theta_\text{min}} es el ángulo de incidencia que se produce a la intensidad mínima, y
• ${\displaystyle \lambda }$ es la longitud de onda de la luz.

Se puede usar un argumento similar para indicar que si imaginamos que la rendija se divide en cuatro, seis, ocho partes, etc., los mínimos se obtienen en ángulos θ_n dados por

${\displaystyle d\,\operatorname {sen} \theta _{n}=n\lambda }$

donde:

• n es un número entero diferente de cero.

No existe un argumento tan simple que nos permita definir los máximos del patrón de difracción. El perfil de intensidad se calcula utilizando la ecuación de difracción de Fraunhofer como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle I(\theta) = I_0 \,\operatorname{sinc}^2 \left( \frac{d \pi}{\lambda} \sin\theta \right)}

donde:

• ${\displaystyle I(\theta )}$ es la intensidad en un ángulo dado,
• Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): I_{0} es la intensidad original, y
• La función sinc no normalizada anterior está dada por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \operatorname{sinc} (x) = \frac{\sin x}{x}} para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle x \neq 0} y ${\displaystyle \operatorname {sinc} (0)=1}$

Este análisis se aplica solo a la aproximación del campo lejano, es decir, a una distancia más grande que la del ancho de la rendija.

Del perfil de intensidad de arriba, si ${\displaystyle d\ll \lambda }$, la intensidad será poco dependiente de ${\displaystyle \theta }$, entonces, el frente de onda que se origina de la ranura se parecería a una onda cilíndrica de intensidad uniforme; Si Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle d \gg \lambda} , solo ${\displaystyle \theta \approx 0}$ tendría una intensidad apreciable, por lo cual, el frente de onda que se origina de la ranura se asemejaría al de la óptica geométrica.

Difracción de luz láser roja de 2 rendijas (arriba) y 5 rendijas.

Difracción de un láser rojo utilizando una rendija de difracción.

Un patrón de difracción de un láser de 633 nm a través de una cuadrícula de 150 rendijas.

Una red de difracción es un componente óptico con un patrón regular. La forma de la luz difractada por una red depende de la estructura de los elementos y el número de elementos presentes, pero toda red tiene máximos de intensidad en los ángulos θ_m que están dados por la ecuación de la red.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle d \left( \sin{\theta_m} + \sin{\theta_i} \right) = m \lambda.}

donde:

• θ_i es el ángulo en qué la luz incide,
• d es la separación de los elementos de la red, y
• m es un número entero que puede ser positivo o negativo.

La luz difractada por una red se puede determinar como la suma de la luz difractada en cada elemento de la red, y es esencialmente una convolución de patrones de difracción e interferencia.

La figura muestra la luz difractada por la red de 2 y 5 elementos donde las distancias entre las rendijas son iguales; se puede ver que los máximos están en la misma posición, pero las estructuras detalladas de las intensidades son diferentes.

Imagen generada por computador de un Disco de Airy.

Patrón de difracción de la luz generado por computador a partir de una abertura circular de 0,5 micrómetros de diámetro a una longitud de onda de 0,6 micrómetros (luz roja) a distancias de 0,1 cm - 1 cm con separaciones de 0,1 cm. Se puede ver la imagen moviéndose desde la región de Fresnel a la región de Fraunhofer donde se ve el patrón de Airy.

La difracción de campo lejano de una onda plana incidente en una abertura circular se conoce a menudo como el Disco de Airy. La variación de la intensidad respecto al ángulo viene dada por:

${\displaystyle I(\theta )=I_{0}\left({\frac {2J_{1}(ka\sin \theta )}{ka\sin \theta }}\right)^{2}}$

donde:

• a es el radio de la abertura circular,
• k es igual a 2π/λ,
• J₁ es la Función de Bessel. Cuanto menor sea la apertura, mayor será el tamaño del punto a una distancia determinada y mayor la divergencia de los rayos difractados.

La onda que emerge de una fuente puntual tiene una amplitud ${\displaystyle \psi }$ en ${\displaystyle \mathbf {r} }$ que viene dada por la solución de la ecuación de onda en el dominio de la frecuencia para una fuente puntual (Ecuación de Helmholtz),

${\displaystyle \nabla ^{2}\psi +k^{2}\psi =\delta (\mathbf {r} )}$

Donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \delta(\mathbf r)} es la función delta tridimensional. La función delta solo tiene dependencia radial, así que el Operador de Laplace (a.k.a. escalar Laplaciano) en el sistema de coordenada esférico simplifica a (coordenadas cilíndricas y esféricas),

${\displaystyle \nabla ^{2}\psi ={\frac {1}{r}}{\frac {\partial ^{2}}{\partial r^{2}}}(r\psi )}$

Por sustitución directa, la solución de esta ecuación puede demostrarse fácilmente que es el escalar de la función de Green, que en el sistema de coordenada esférico (y utilizando la convención de tiempo de la física ${\displaystyle e^{-i\omega t}}$) es:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \psi(r) = \frac{e^{ikr}}{4 \pi r}}

Esta solución supone que la fuente de la función delta se encuentra en el origen. Si la fuente se encuentra en un punto de origen arbitrario, denotado por el vector ${\displaystyle \mathbf {r} '}$y el punto de campo está localizado en el punto ${\displaystyle \mathbf {r} }$, entonces podemos representar el escalar de la función de Green (para la ubicación de la fuente arbitraria) como:

${\displaystyle \psi (\mathbf {r} |\mathbf {r} ')={\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{4\pi |\mathbf {r} -\mathbf {r} '|}}}$

Por tanto, si un campo eléctrico, E_inc(x,y) incide en la abertura, el campo producido por esta distribución de la abertura está dada por la integral de superficie:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \Psi(r)\propto \iint\limits_\mathrm{aperture} E_\mathrm{inc}(x',y')~ \frac{e^{ik | \mathbf r - \mathbf r'|}}{4 \pi | \mathbf r - \mathbf r' |} \,dx'\, dy',}

Cálculo de los campos de la región de Fraunhofer.

Donde el punto de origen en la abertura está dado por el vector

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \mathbf{r}' = x' \mathbf{\hat{x}} + y' \mathbf{\hat{y}}}

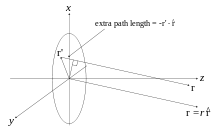
En el campo lejano, donde se puede emplear la aproximación de los rayos paralelos, la función de Green,

${\displaystyle \psi (\mathbf {r} |\mathbf {r} ')={\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{4\pi |\mathbf {r} -\mathbf {r} '|}}}$

Se simplifica a

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \psi(\mathbf{r} | \mathbf{r}') = \frac{e^{ik r}}{4 \pi r} e^{-ik ( \mathbf{r}' \cdot \mathbf{\hat{r}})}}

como se puede ver en la figura de la derecha (click para ampliar).

La expresión para el campo de la zona lejana (región de Fraunhofer) se convierte en

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \Psi(r)\propto \frac{e^{ik r}}{4 \pi r} \iint\limits_\mathrm{aperture} E_\mathrm{inc}(x',y') e^{-ik ( \mathbf{r}' \cdot \mathbf{\hat{r}} ) } \, dx' \,dy',}

Ahora, ya que

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \mathbf{r}' = x' \mathbf{\hat{x}} + y' \mathbf{\hat{y}}}

Y

${\displaystyle \mathbf {\hat {r}} =\sin \theta \cos \phi \mathbf {\hat {x}} +\sin \theta ~\sin \phi ~\mathbf {\hat {y}} +\cos \theta \mathbf {\hat {z}} }$

la expresión para el campo de la región de Fraunhofer de una abertura plana se convierte,

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \Psi(r)\propto \frac{e^{ik r}}{4 \pi r} \iint\limits_\mathrm{aperture} E_\mathrm{inc}(x',y') e^{-ik \sin \theta (\cos \phi x' + \sin \phi y')} \, dx'\, dy'}

Siendo,

${\displaystyle k_{x}=k\sin \theta \cos \phi \,\!}$

Y

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle k_y = k \sin \theta \sin \phi \,\!}

el campo de la región de Fraunhofer de la abertura plana asume la forma de una transformada de Fourier

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \Psi(r)\propto \frac{e^{ik r}}{4 \pi r} \iint\limits_\mathrm{aperture} E_\mathrm{inc}(x',y') e^{-i (k_x x' + k_y y') } \,dx'\, dy',}

En el campo lejano / región de Fraunhofer, esto se convierte en la transformada espacial de Fourier de la distribución de la apertura. El principio de Huygens, cuando se aplica a una apertura, dice simplemente que el patrón de difracción de campo lejano es la transformada espacial de Fourier de la forma de la apertura, y esto es un subproducto directo del uso de la aproximación de rayos paralelos, que es idéntico a hacer una descomposición de onda plana de los campos planos de la apertura (véase la óptica de Fourier).

La forma en que el perfil de un rayo láser cambia a medida que se propaga está determinada por la difracción. Cuando todo el haz emitido tiene un frente de onda plano y espacialmente coherente, se aproxima al perfil del haz Gaussiano y tiene la menor divergencia para un diámetro determinado. El más pequeño la viga de producción, el más rápido diverge. Cuanto más pequeño es el rayo de salida, más rápido se desvía. Es posible reducir la divergencia de un rayo láser expandiéndolo primero con una lente convexa y luego colimándolo con una segunda lente convexa cuyo punto focal coincide con el de la primera lente. El rayo resultante tiene un diámetro mayor, y por lo tanto una menor divergencia. La divergencia de un rayo láser puede reducirse por debajo de la difracción de un rayo gaussiano o incluso invertirse hasta la convergencia si el índice de refracción del medio de propagación aumenta con la intensidad de la luz.[12] Esto puede dar lugar a un efecto de autoenfoque.

Cuando el frente de onda del haz emitido tiene perturbaciones, solo la longitud de coherencia transversal (en la que la perturbación del frente de onda es inferior a 1/4 de la longitud de onda) debe considerarse como un diámetro de haz gaussiano al determinar la divergencia del haz láser. Si la longitud de coherencia transversal en la dirección vertical es mayor que en la horizontal, la divergencia del rayo láser será menor en la dirección vertical que en la horizontal.

El disco de Airy alrededor de cada una de las estrellas de la apertura del telescopio de 2,56 m puede verse en esta imagen afortunada de la estrella binaria zeta Boötis.

La capacidad de un sistema de imágenes para resolver los detalles está limitada en última instancia por la difracción. Esto se debe a que una onda plana incidente en una lente o espejo circular se difracta como se describe anteriormente. La luz no está enfocada a un punto sino que forma un Disco de Airy que tiene un punto central en el plano focal con un primer radio nulo de

${\displaystyle d=1.22\lambda N,\,}$

donde λ es la longitud de onda de la luz y N es el número f (longitud focal dividida por el diámetro) de la óptica de imágenes. En el espacio de los objetos la resolución angular correspondiente es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle \sin \theta = 1.22 \frac{\lambda}{D},\, }

donde D es el diámetro de la pupila de entrada del lente de la imagen (por ejemplo, del espejo principal de un telescopio).

Dos fuentes puntuales producirán cada una un patrón de Airy —ver la foto de una estrella binaria—. A medida que las fuentes puntuales se acercan entre sí, los patrones comenzarán a superponerse, y finalmente se fusionarán para formar un solo patrón, en cuyo caso las dos fuentes puntuales no pueden resolverse en la imagen. El criterio de Rayleigh especifica que dos fuentes puntuales pueden considerarse resolubles si la separación de las dos imágenes es al menos el radio del disco de Airy, es decir, si el primer mínimo de una coincide con el máximo de la otra.

Así, cuanto mayor sea la apertura de la lente, y cuanto menor sea la longitud de onda, más fina será la resolución de un sistema de imágenes. Por eso los telescopios tienen lentes o espejos muy grandes, y por eso los microscopios ópticos están limitados en el detalle que pueden ver.

El patrón de manchas que se ve cuando se usa un puntero láser es otro fenómeno de difracción. Es el resultado de la superposición de muchas ondas con diferentes fases, que se producen cuando un rayo láser ilumina una superficie rugosa. Se suman para dar una onda resultante cuya amplitud, y por lo tanto la intensidad, varía al azar.

El principio de Babinet es un teorema útil que afirma que el patrón de difracción de un cuerpo opaco es idéntico al de un agujero del mismo tamaño y forma, pero con diferentes intensidades. Esto significa que las condiciones de interferencia de una sola obstrucción serían las mismas que las de una sola rendija.