Fatiga de materiales
En ingeniería y, en especial, en ciencia de los materiales, la fatiga de materiales se refiere a un fenómeno por el cual la rotura de los materiales bajo cargas dinámicas cíclicas se produce más fácilmente que con cargas estáticas. Aunque es un fenómeno que, sin definición formal, era reconocido desde la antigüedad, este comportamiento no fue de interés real hasta la revolución industrial, cuando a mediados del siglo XIX se comenzaron a producir las fuerzas necesarias para provocar la rotura de los materiales con cargas dinámicas muy inferiores a las necesarias en el caso estático y a desarrollar métodos de cálculo para el diseño de piezas confiables. Este no es el caso de materiales de aparición reciente, para los que es necesaria la fabricación y el ensayo de prototipos.
- Denominado ciclo de carga repetida, los máximos y mínimos son asimétricos con respecto al nivel cero de carga.
- Aleatorio: el nivel de tensión puede variar al azar en amplitud y frecuencia.
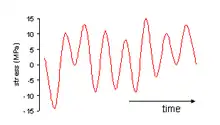
La amplitud de la tensión varía alrededor de un valor medio, el promedio de las tensiones máxima y mínima en cada ciclo:
El intervalo de tensiones es la diferencia entre tensión máxima y mínima
La amplitud de tensión es la mitad del intervalo de tensiones
El cociente de tensiones R es el cociente entre las amplitudes mínima y máxima
Por convención, los esfuerzos a tracción son positivos y los de compresión son negativos. Para el caso de un ciclo con inversión completa de carga, el valor de R es igual a -1.
Etapas de fatiga
Históricamente, la fatiga ha sido separada en:
- región de fatiga de altos ciclos: que requieren más de 104 ciclos para la falla, en el cual el esfuerzo es bajo y, primeramente, elástico.
- región de fatiga de bajos ciclos: en la cual es, significantemente, plástico. Experimentos han demostrado que la fatiga de bajos ciclos, también, es crecimiento de fractura.
Las fallas por fatiga, ambas para altos y bajos ciclos, todas siguen las mismas etapas básicas:
- inicio de ruptura
- crecimiento de ruptura: Etapa (I) y Etapa (II)
- falla
Para comenzar el proceso, las rupturas se deben nuclear en un material. Este proceso puede ocurrir tanto por concentración de esfuerzos en muestras metálicas o en áreas con alta densidad de huecos en muestras de polímeros. Primeramente, estas rupturas se propagan despacio, durante el crecimiento de ruptura en la etapa (I) a lo largo de planos cristalográficos, en los cuales los esfuerzos de corte son los más altos. Una vez que la ruptura alcanzó el tamaño crítico, se propagan rápidamente durante la etapa (II) del crecimiento de ruptura en una dirección perpendicular a la fuerza aplicada. Estas rupturas pueden, eventualmente, llevar a la falla última del material, a menudo, en una forma quebradiza catastrófica.
Inicio de ruptura
La formación de rupturas iniciales que preceden a la falla por fatiga es un proceso separado que consiste de cuatro etapas discretas en muestras metálicas:
- El material desarrollará estructuras de celda y se endurece en respuesta a la carga aplicada. Esto causa que la amplitud de esfuerzos aplicados incremente dando nuevas restricciones en deformación.
- Estas nuevas estructuras de celda, eventualmente, se romperán con la formación de bandas de deslizamiento persistente (ing. "persistent slip bands, PSBs"). El deslizamiento en el material esta localizado en estas PSBs, y el deslizamiento exagerado puede ahora servir como un concentrador de esfuerzo para que una ruptura se forme.
- La nucleación y crecimiento de una ruptura hasta un tamaño detectable cuenta por mucho del proceso de ruptura. Es por esta razón que las fallas de fatiga cíclica parecen ocurrir de repente donde el total de los cambios en el material no son visibles sin pruebas destructivas. Aun, normalmente, en materiales dúctiles, las fallas por fatiga asemejarán fallas frágiles repentinas.
Los planos deslizantes inducidos por PSB resultan en intrusiones y extrusiones a lo largo de la superficie de un material, a menudo, ocurren en pares. Este deslizamiento no es un cambio microestructural en el material, pero, más una propagación de dislocaciones en el material. En lugar de una interface suave, las intrusiones y extrusiones causarán que la superficie del material se asemeje al borde de un mazo de cartas, en la cual no todas las cartas están perfectamente alineadas. Las intrusiones y extrusiones inducidas por deslizamiento crean estructuras de superficie extremadamente fina en el material. Con tamaño de estructura de superficie inversamente relacionada con factores de concentración de esfuerzo, el deslizamiento de superficie inducida por PSB pueden causar que inicien las rupturas.
Estas etapas, también, se pueden pasar por alto, enteramente, si las rupturas se forman desde el concentrador de esfuerzo preexistente, tal como una inclusión en el material, o desde un concentrador de esfuerzo geométrico causado por una esquina interna aguda o filete.
Crecimiento de ruptura
Mucho de la vida de la fatiga es, generalmente, consumido en la fase de crecimiento de ruptura. La tasa de crecimiento es, primeramente, manejada por el rango de carga cíclica, aunque factores adicionales tales como esfuerzo medio, medio ambiente, sobrecarga y baja carga pueden, también, afectar la tasa de crecimiento. El crecimiento de ruptura podrá detenerse, si las cargas son suficientemente pequeñas para caer bajo un umbral crítico.
Las rupturas por fatiga pueden crecer debido a defectos de material o fabricación, tan pequeños como 10 μm.
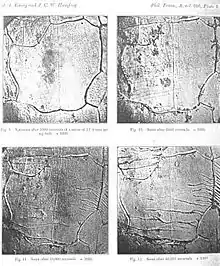
Cuando la tasa de crecimiento llega a ser suficientemente grande, las estrías de fatiga pueden ser vistas en la superficie de ruptura. Las estrías marcan la posición del comienzo de ruptura y el espesor de cada estría representa el crecimiento de un ciclo de carga. Las estrías son un resultado de la plasticidad en el comienzo de ruptura.
Cuando la intensidad de esfuerzo excede un valor crítico conocido como tenacidad de ruptura, ocurrirá la ruptura rápida insostenible, usualmente, por un proceso de Coalescencia microvoide. Antes de la ruptura final, la superficie de la ruptura podrá contener una mezcla de áreas de fatiga y ruptura rápida.
Falla
Al mismo tiempo que la grieta aumenta en anchura, el extremo avanza por continua deformación por cizalladura hasta que alcanza una configuración enromada. Se alcanza una dimensión crítica de la grieta y se produce la rotura.
La región de una superficie de fractura que se formó durante la etapa II de propagación puede caracterizarse por dos tipos de marcas, denominadas marcas de playa y estrías. Ambas indican la posición del extremo de la grieta en diferentes instantes y tienen el aspecto de crestas concéntricas que se expanden desde los puntos de iniciación. Las marcas de playa son macroscópicas y pueden verse a simple vista.
Las marcas de playa y estrías no aparecen en roturas rápidas.
Velocidad de propagación
Los resultados de los estudios de fatiga han mostrado que la vida de un componente estructural puede relacionarse con la velocidad de crecimiento de la grieta. La velocidad de propagación de la grieta es una función del nivel de tensión y de la amplitud de la misma.
| Símbolo | Nombre | Unidad |
|---|---|---|
| C | Constantes para un determinado material | |
| m | Constantes para un determinado material (entre 1 y 6) | |
| K | Factor de intensidad de tensiones | |
| da / dN | Pendiente de la curva de velocidad de crecimiento |
o bien
Desarrollando estas expresiones a partir de gráficas generadas por ellas mismas, se puede llegar a la siguiente ecuación:
| Símbolo | Nombre | Unidad |
|---|---|---|
| Nf | Número de ciclos hasta rotura | |
| Y | Parámetro independiente de la longitud de la grieta | |
| m | Constantes para un determinado material | |
| C | Constantes para un determinado material | |
| ac | Longitud crítica de la grieta | |
| a0 | Longitud de grieta inicial |
| Símbolo | Nombre | Unidad |
|---|---|---|
| K1c | Tenacidad de fractura de deformaciones planas |
Estas fórmulas fueron generadas por Paul C. Paris en 1961 realizando una gráfica logarítmica log-log de la velocidad de crecimiento de grieta contra el factor de intensidad de tensiones mostrando una relación lineal en la gráfica. Utilizando esta gráfica se pueden realizar predicciones cuantitativas sobre la vida residual de una probeta dado un tamaño de grieta particular. Se encuentra así el comienzo de la iniciación o iniciación rápida de grieta.
Características de fatiga
- En aleaciones de metal, y para el caso de simplificación cuando no hay discontinuidades macroscópicas o microscópicas, el proceso comienza con movimiento de dislocaciones en el nivel microscópico, el cual, eventualmente, forma bandas de deslizamiento persistente que llega a ser el núcleo de pequeñas rupturas.
- Las discontinuidades macroscópicas y microscópicas (en la escala de grano cristalino) tanto como características de diseño de componentes que causa concentración de esfuerzos (agujeros, chaveteros, cambios agudos de dirección de carga, etc.) son ubicaciones comunes en las cuales el proceso de fatiga comienza.
- La fatiga es un proceso que tiene un grado de aleatoriedad (estocástico), a menudo, mostrando considerable dispersión, aún en muestras idénticas parecidas en ambientes bien controlados.
- La fatiga es usualmente asociada con esfuerzos de tensión pero las rupturas por fatiga han sido reportadas debido a cargas compresivas.
- A mayor rango de esfuerzos aplicados, menor la vida.
- La dispersión de vida de fatiga tiende a incrementar para mayor vida de fatiga.
- Daño es irreversible. Los materiales no se recuperan cuando descansan.
- La vida de fatiga es influenciada por una variedad de factores, tales como temperatura, acabado superficial, microestructura metalúrgica, presencia de químicos oxidantes o inertes, esfuerzos residuales, contacto rasposo (fretting), etc.
- Algunos materiales, (ejemplo, algunos aceros y aleaciones de titanio) exhiben un límite de fatiga teórico abajo del cual la carga continuada no lleva a la falla por fatiga.
- El límite de fatiga de alto ciclo (cerca de 104 a 108 ciclos) puede ser descrito por parámetros basados en esfuerzo. Un aparejo de prueba servo-hidráulica controlada por carga es, comúnmente, utilizada en estas pruebas, con frecuencias alrededor de 20 - 50 Hz. Otro tipo de máquinas (como máquinas de resonancia magnética) pueden, también, ser utilizadas para alcanzar frecuencias arriba de 250 Hz.
- La fatiga de ciclo bajo (carga que típicamente causa falla en menos que 104 ciclos) esta asociada con comportamiento plástico localizado en metales, así, un parámetro basado en deformación debería ser utilizado para predicciones de vida de fatiga en metales. Las pruebas son conducidas con amplitudes de deformación constante, típicamente, 0.01 - 5 Hz.
Línea temporal de historia de investigación
| Año | Acontecimiento |
|---|---|
| 1837 | Wilhelm Albert publica el primer artículo sobre fatiga. Él ideó una máquina de prueba para las cadenas transportadoras utilizadas en las minas Clausthal. |
| 1839 | Jean-Victor Poncelet describe los metales como siendo agotados en sus lecturas en la escuela militar en Metz. |
| 1842 | William John Macquorn Rankine reconoce la importancia de la concentración de esfuerzos en sus investigaciones de falla de eje de locomotora. El Accidente ferroviario de Versalles fue causado por falla de fatiga del eje de locomotora. |
| 1843 | Joseph Glynn reporta sobre la fatiga de un eje en un ténder de locomotora. Él identificó el chavetero como el origen de ruptura. |
| 1848 | La Railway Inspectorate reporta una de las primeras fallas de rueda, probablemente de un agujero de remache en la huella de rueda de carruaje de ferrocarril. Era como una falla de fatiga. |
| 1849 | A Eaton Hodgkinson se le otorgó una "pequeña suma de dinero" por reportar al Parlamento del RU en su trabajo en "ascertaining by direct experiment, the effects of continued changes of load upon iron structures and to what extent they could be loaded without danger to their ultimate security". |
| 1854 | F. Braithwaite reporta sobre fallas de fatiga de servicio común y acuña el término fatiga. |
| 1860 | Pruebas de fatiga sistemáticas emprendidas por Sir William Fairbairn y August Wöhler. |
| 1870 | A. Wöhler sumariza su trabajo en ejes de locomotora. Concluyó que el rango de esfuerzos cíclicos es más importante que el esfuerzo pico e introdujo el concepto de límite de fatiga. |
| 1903 | Sir James Alfred Ewing demuestra el origen de la falla de fatiga en rupturas microscópicas. |
| 1910 | O. H. Basquin propone una relación log-log para las curvas S-N, utilizando datos de prueba de Wöhler. |
| 1940 | Sidney M. Cadwell publica el primer estudio riguroso de fatiga en caucho. |
| 1945 | A. M. Miner populariza la hipótesis de daño lineal de Palmgren (1924) como una herramienta práctica de diseño. |
| 1952 | W. Weibull, un modelo de curva S-N |
| 1954 | El primer avión de reacción comercial, el De Havilland Comet, sufre un desastre al romperse en el aire, tres planos, causando que De Havilland y los demás fabricantes rediseñen los aviones de alta altitud y, en particular, reemplacen las aberturas cuadradas, como en ventanas, con ovaladas. |
| 1954 | L. F. Coffin y S. S. Manson explican el crecimiento de ruptura de fatiga en términos de deformación plástica en la punta de la ruptura |
| 1961 | P. C. Paris propone métodos de predicción de la tasa de crecimiento de rupturas de fatiga individual en la cara de escepticismo inicial y defensa popular de la aproximación fenomenológica de Miner. |
| 1968 | Tatsuo Endo y M. Matsuishi idean un algoritmo de conteo de flujo de lluvia y permite la aplicación confiable de la regla de Miner a cargas aleatorias. |
| 1970 | Smith, Watson y Topper desarrollan un modelo de corrección de esfuerzo medio, en el cual el daño por fatiga en un ciclo es determinado por el producto del esfuerzo máximo y amplitud de deformación. |
| 1973 | M. W. Brown y K. J. Miller observan que la vida de fatiga bajo condiciones multiaxiales esta gobernada por la experiencia de un plano que recibe el mayor daño, y que ambas cargas de tensión y corte en el plano crítico deben ser consideradas |
| 2001 | Kohout y Věchet sugieren un rango total de curvas S-N basado en el parámetro de daño de esfuerzo cubriendo regiones de ciclos desde el esfuerzo de tensión al límite de fatiga permanente. |
| 2001 | Enrique Castillo y Alfonso Fernández-Canteli presentaron una forma particular de modelo probabilístico para materiales bajo fatiga en cual acuerpa características Weibull y el efecto de medida en un marco de eslabón más débil. |
Prediciendo la vida de fatiga
La American Society for Testing and Materials define la vida de fatiga (), como el número de ciclos de esfuerzo de un carácter específico que una muestra sostiene antes que la falla de una naturaleza específica ocurra. Para algunos materiales, notablemente, acero y titanio, hay un valor teórico para la amplitud de esfuerzo, bajo el cual el material no fallará para cualquier número de ciclos, llamado límite de fatiga. Sin embargo, en la práctica, algunos cuerpos de trabajo sometidos a un gran número de ciclos, sugieren que los limites de fatiga no existen para ningún metal.
Los ingenieros han utilizado un número de métodos para determinar la vida de fatiga de un material:
- Método de vida de esfuerzo
- Método de vida de deformación
- Método de crecimiento de ruptura
- Métodos probabilísticos, los cuales pueden estar basados tanto en métodos de vida o crecimiento de ruptura.
Si se utiliza la aproximación de vida de esfuerzo / deformación o la aproximación de crecimiento de ruptura, la carga de amplitud compleja o variable se reduce a una serie cargas cíclicas simples equivalente utilizando para ello, una técnica tal como el algoritmo de conteo de flujo de lluvia.
Métodos de vida de esfuerzos y vida de deformación
Una parte mecánica es, a menudo, expuesta a una compleja, a menudo, aleatoria, secuencia de cargas grandes y pequeñas. En orden de evaluar la vida segura de tal parte, utilizando el daño por fatiga o método de vida esfuerzo / deformación, usualmente, se realiza la siguiente serie de pasos:
- La carga compleja es reducida a una serie de cargas cíclicas simples utilizando una técnica tal como análisis de flujo de lluvia
- Un histograma de esfuerzos cíclicos es creado desde el análisis de flujo de lluvia para formar un espectro de daño por fatiga
- Para cada nivel de esfuerzo, el grado de daño acumulado es calculado por una curva S-N
- Los efectos de las contribuciones individuales son combinados utilizando un algoritmo tal como la regla de Miner
Ya que, las curvas S-N son, típicamente, generadas para carga uniaxial, se necesita alguna regla equivalente, cuando la carga es multiaxial. Para historias de carga proporcional simple (carga lateral, en una razón constante, con la axial), se debe aplicar la regla de Sines. Para situaciones más complejas, tales como cargas no proporcionales, se debe aplicar el análisis de plano crítico.
Regla de Miner
En 1945, M. A. Miner popularizó la regla que, primeramente, había sido propuesta por A. Palmgren en 1924. La regla, llamada regla de Miner o Hipótesis de daño lineal Palmgren-Miner, establece que donde haya magnitudes de esfuerzo diferente () en un espectro , cada ciclo contribuye . Entonces, si es el número de ciclos para la falla de un esfuerzo constante (determinado por pruebas de fatiga uni-axial), la falla ocurre cuando:
Usualmente, para propósitos de diseño, () se asume como 1. Esto se puede pensar como evaluando que proporción de vida es consumida por una combinación lineal de esfuerzos a magnitudes variables.
Aunque la regla de Miner puede ser una aproximación útil en muchas circunstancias, tiene varias grandes limitaciones:
- Falla en reconocer la naturaleza probabilística de la fatiga y no hay un camino simple para relacionar la vida predicho por la regla con las características de una distribución de probabilidad. Los analistas industriales, a menudo, utilizan curvas de diseño, ajustadas para contar por dispersión, para calcular .
- La secuencia en la cual ciclos de esfuerzo altos vrs. bajos son aplicados a una muestra, de hecho, afecta la vida de fatiga, para la cual la regla de Miner no cuenta. En algunas circunstancias, los ciclos de esfuerzo bajo seguidos por esfuerzos altos causan más daño que podría ser predicho por la regla. No considera el efecto de una sobrecarga por esfuerzo alto que puede resultar en un esfuerzo residual compresivo que pude retardar el crecimiento de ruptura. El esfuerzo alto seguido por esfuerzo bajo puede tener menos daño debido a la presencia de esfuerzos residuales compresivos (o daño plástico localizado alrededor del inicio de ruptura).
Método vida de esfuerzo (S-N)
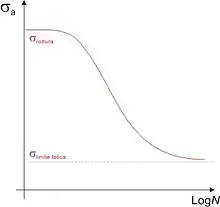
El desempeño de fatiga de materiales es, comúnmente, caracterizado por una curva S-N, también llamada curva Wöhler. Esta es, a menudo, trazada con el esfuerzo cíclico () contra los ciclos de falla () en una escala logarítmica. Las curvas S-N se derivan de pruebas en muestras del material a ser caracterizado (a menudo, llamado cupones o especímenes), en las cuales un esfuerzo sinusoidal regular es aplicado por una máquina de pruebas, la cual también cuenta el número de ciclos para la falla Este proceso es, algunas veces, llamado como prueba cupón (ing. coupon testing). Para mayor precisión pero baja generalidad, se utiliza la prueba de componente. Cada cupón o prueba de componente genera un punto en el trazado, aunque en algunos casos hay un agotamiento, en donde el tiempo de falla excede aquel disponible para la prueba (vea censoring). El análisis de datos de fatiga requiere técnicas de estadística, especialmente análisis de sobrevivencia y regresión lineal.
La progresión de la curva S-N puede ser influenciada por varios factores tales como la razón de esfuerzo (esfuerzo medio), frecuencia de carga, temperatura, corrosión, esfuerzos residuales, y la presencia de muescas. Una diagrama de vida de fatiga constante (ing. constant fatigue life, CFL diagram) es útil para el estudio del efecto de razón de esfuerzo. La línea Goodman es un método utilizado para estimar la influencia del esfuerzo medio en el limite de fatiga.
Un diagrama vida de fatiga constante (CFL) es útil para el efecto de razón de esfuerzo en la curva S-N. También, en la presencia de un esfuerzo estable superpuesto en la carga cíclica, la relación de Goodman puede ser utilizada para estimar una condición de falla. Traza amplitud de esfuerzo contra esfuerzo medio con el límite de fatiga y el esfuerzo de tensión último del material como los dos extremos. El criterio de falla alternativo incluye Soderberg y Gerber.
Como cupones muestreados de un marco homogéneo desplegarán una variación en su número de ciclos para la falla, la curva S-N, más apropiadamente, podría ser una curva de Probabilidad de ciclo de esfuerzo (S-N-P) para capturar la probabilidad de falla después de un número dado de ciclos de un cierto esfuerzo.
La curva s-n, también llamada curva de Wöhler, se obtienen a través de una serie de ensayos donde una probeta del material se somete a tensiones cíclicas con una amplitud máxima relativamente grande (aproximadamente 2/3 de la resistencia estática a tracción). Se cuentan los ciclos hasta rotura. Este procedimiento se repite en otras probetas a amplitudes máximas decrecientes.
Los resultados se representan en un diagrama de tensión, S, frente al logaritmo del número N de ciclos hasta la rotura para cada una de las probetas. Los valores de S se toman normalmente como amplitudes de la tensión .
Se pueden obtener dos tipos de curvas S-N. A mayor tensión, menor número de ciclos hasta rotura. En algunas aleaciones férreas y en aleaciones de titanio, la curva S-N se hace horizontal para valores grandes de N, es decir, existe una tensión límite, denominada límite de fatiga, por debajo del cual la rotura por fatiga no ocurrirá.
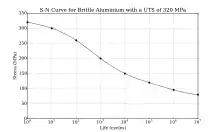
Suele decirse, de manera muy superficial, que muchas de las aleaciones no férreas (aluminio, cobre, magnesio, etc.) no tienen un límite de fatiga, dado que la curva S-N continúa decreciendo al aumentar N. Según esto, la rotura por fatiga ocurrirá independientemente de la magnitud de la tensión máxima aplicada y, por tanto, para estos materiales, la respuesta a fatiga se especificaría mediante la resistencia a la fatiga que se define como el nivel de tensión que produce la rotura después de un determinado número de ciclos. Sin embargo, esto no es exacto: es ingenuo creer que un material se romperá al cabo de tantos ciclos, no importa cuán ridículamente pequeña sea la tensión presente.
En rigor, todo material cristalino (metales, …) presenta un límite de fatiga. Ocurre que para materiales como la mayoría de los férricos, dicho límite suele situarse en el entorno del millón de ciclos (para ensayos de probeta rotatoria), para tensiones internas que rondan 0,7-0,45 veces el límite elástico del material; mientras que para aquellos que se dicen sin límite de fatiga, como el aluminio, se da incluso para tensiones muy bajas (en el aluminio, de 0,1-0,2 veces dicho límite), y aparece a ciclos muy elevados (en el aluminio puede alcanzar los mil millones de ciclos; en el titanio pueden ser, según aleaciones, cien millones de ciclos o incluso, excepcionalmente el billón de ciclos). Como en general no se diseñan máquinas ni elementos de manera que las máximas tensiones sean de 0,1-0,2 veces el límite elástico del material, pues en ese caso se estarían desaprovechando buena parte de las capacidades mecánicas del material, y como tampoco se suele diseñar asumiendo valores de vida por encima del millón de ciclos, en la práctica este tipo de materiales no van a poder presentar su límite de fatiga, aunque sí lo tienen.
Esta confusión surge de la propia naturaleza de las curvas S-N de Wöhler, que fueron concebidas en el siglo XIX para los aceros. Al ampliarse el tipo de materiales metálicos usuales en ingeniería, los mismos conceptos y las mismas curvas se trasladaron a otros metales cuyo comportamiento a fatiga es esencialmente diferente (de hecho, es una característica propia de la fatiga la gran variabilidad de comportamientos que presenta en los distintos tipos de materiales). Y como quiera que el acero ha sido y es la piedra angular de la ingeniería, interesaba comparar las propiedades de los demás metales con respecto al mismo: es y era común que, al ensayar materiales, los ensayos se suspendieran una vez superado el millón de ciclos, considerando que no interesaba caracterizar materiales por encima de ese límite temporal.
Otro parámetro importante que caracteriza el comportamiento a fatiga de un material es la vida a fatiga Nf. Es el número de ciclos para producir una rotura a un nivel especificado de tensiones.[1]
Además, el conocimiento del comportamiento a fatiga no es igual en todos los materiales: el material mejor conocido, más ensayado y más fiable en cuanto a predicciones a fatiga es la familia de los aceros. De otros materiales metálicos de uso común como el aluminio, el titanio, aleaciones de cobre, níquel, magnesio o cromo, se dispone de menos información (decreciente esta con la novedad de la aleación), aunque la forma de los criterios de cálculo a fatiga y de las curvas S-N parece regular, y es parecida a la de los de los aceros, y se considera que su fiabilidad es alta. Para materiales cerámicos, por el contrario, se dispone de muy poca información, y de hecho, el estudio de la fatiga en ellos y en polímeros y materiales compuestos es un tema de candente investigación actual.
En todo caso, existe una diferencia notable entre la teoría y la realidad. Esto conduce a incertidumbres significativas en el diseño cuando la vida a fatiga o el límite de fatiga son considerados. La dispersión en los resultados es una consecuencia de la sensibilidad de la fatiga a varios parámetros del ensayo y del material que son imposibles de controlar de forma precisa. Estos parámetros incluyen la fabricación de las probetas y la preparación de las superficies, variables metalúrgicas, alineamiento de la probeta en el equipo de ensayos, tensión media y frecuencia de carga del ensayo.
Aproximadamente la mitad de las probetas ensayadas se rompen a niveles de tensión que están cerca del 25% por debajo de la curva. Esto suele asociarse a la presencia de fuentes de concentración de tensiones internas, tales como defectos, impurezas, entallas, ralladuras, …, que han permanecido indetectadas.
Se han desarrollado técnicas estadísticas y se han utilizado para manejar este fallo en términos de probabilidades. Una manera adecuada de presentar los resultados tratados de esta manera es con una serie de curvas de probabilidad constante.
| Fatiga | Ciclos |
|---|---|
| Bajo número de ciclos (oligofatiga) | < 103 - 105 |
| Alto número de ciclos | > 103 - 105 |
Factores que intervienen
.jpg.webp)
Son diversos los factores que intervienen en un proceso de rotura por fatiga aparte de las tensiones aplicadas. Así pues, el diseño, tratamiento superficial y endurecimiento superficial pueden tener una importancia relativa.
Diseño
El diseño tiene una influencia grande en la rotura de fatiga. Cualquier discontinuidad geométrica actúa como concentradora de tensiones y es por donde puede nuclear la grieta de fatiga. Cuanto más aguda es la discontinuidad, más severa es la concentración de tensiones.
La probabilidad de rotura por fatiga puede ser reducida evitando estas irregularidades estructurales, o sea, realizando modificaciones en el diseño, eliminando cambios bruscos en el contorno que conduzcan a cantos vivos, por ejemplo, exigiendo superficies redondeadas con radios de curvatura mayores.
Las dimensiones de la pieza también influyen, aumentando el tamaño de la misma obtenemos una reducción en el límite de fatiga.
Tratamientos superficiales
En las operaciones de mecanizado, se producen pequeñas rayas y surcos en la superficie de la pieza por acción del corte. Estas marcas limitan la vida a fatiga pues son pequeñas grietas las cuales son mucho más fáciles de aumentar. Mejorando el acabado superficial mediante pulido aumenta la vida a fatiga.
Uno de los métodos más efectivos de aumentar el rendimiento es mediante esfuerzos residuales de compresión dentro de una capa delgada superficial. Cualquier tensión externa de tracción es parcialmente contrarrestada y reducida en magnitud por el esfuerzo residual de compresión. El efecto neto es que la probabilidad de nucleación de la grieta, y por tanto de rotura por fatiga se reduce.
Este proceso se llama «granallado» o «perdigonado». Partículas pequeñas y duras con diámetros del intervalo de 0,1 a 1,0 mm son proyectadas a altas velocidades sobre la superficie a tratar. Esta deformación induce tensiones residuales de compresión.
Endurecimiento superficial
Es una técnica por la cual se aumenta tanto la dureza superficial como la vida a fatiga de los aceros aleados. Esto se lleva a cabo mediante procesos de carburación y nitruración, en los cuales un componente es expuesto a una atmósfera rica en carbono o en nitrógeno a temperaturas elevadas. Una capa superficial rica en carbono en nitrógeno es introducida por difusión atómica a partir de la fase gaseosa. Esta capa es normalmente de 1mm de profundidad y es más dura que el material del núcleo. La mejora en las propiedades de fatiga proviene del aumento de dureza dentro de la capa, así como de las tensiones residuales de compresión que se originan en el proceso de cementación y nitruración.
Influencia del medio
El medio puede afectar el comportamiento a fatiga de los materiales. Hay dos tipos de fatiga por el medio: fatiga térmica y fatiga con corrosión.
Fatiga térmica
La fatiga térmica se induce normalmente a temperaturas elevadas debido a tensiones térmicas fluctuantes; no es necesario que estén presentes tensiones mecánicas de origen externo. La causa de estas tensiones térmicas es la restricción a la dilatación y o contracción que normalmente ocurren en piezas estructurales sometidas a variaciones de temperatura. La magnitud de la tensión térmica resultante debido a un cambio de temperatura depende del coeficiente de dilatación térmica y del módulo de elasticidad.
Fatiga estática (corrosión-fatiga)
La fatiga con corrosión ocurre por acción de una tensión cíclica y ataque químico simultáneo. Lógicamente los medios corrosivos tienen una influencia negativa y reducen la vida a fatiga, incluso la atmósfera normal afecta a algunos materiales. A consecuencia pueden producirse pequeñas fisuras o picaduras que se comportarán como concentradoras de tensiones originando grietas. La propagación también aumenta en el medio corrosivo puesto que el medio corrosivo también corroerá el interior de la grieta produciendo nuevos concentradores de tensión.
Fatiga de materiales compuestos
Los materiales compuestos pueden ofrecer excelente resistencia a la carga por fatiga. En general, los materiales compuestos exhiben buena tenacidad a la fractura y, a diferencia de los metales, incrementan la tenacidad a la fractura con incremento de fortaleza. El tamaño de daño crítico en materiales compuestos es, también, más grande que para los metales.
El modo primario para daño en una estructura metálica es agrietamiento. Para metal, las rupturas se propagan en una forma relativamente bien definida con respecto al esfuerzo aplicado, y el tamaño de ruptura crítica y tasa de propagación de ruptura pueden ser relacionados con los datos de espécimen a través de mecánica de fractura analítica. Sin embargo, con estructuras de material compuesto, no hay un modo de daño simple, el cual domine. Agrietamiento matricial, delaminación, separado, huecos, fractura de fibra, y agrietamiento de material compuesto todos pueden ocurrir separadamente y en combinación, y la predominancia de uno o más es altamente dependiente en la orientación de las láminas y condiciones de carga. En adición, las únicas articulaciones y adjuntos utilizados para estructuras de material compuesto, a menudo, introducen modos de falla diferentes de aquellos tipificados por el laminado mismo.
El daño del material compuesto se propaga en una forma menos regular y los modos de daño pueden cambiar. La experiencia con materiales compuestos indica que la tasa de propagación de daño no exhibe las dos regiones distintas de inicio y propagación como en los metales. El rango de inicio de ruptura en metales es propagación, y hay una diferencia significativa cuantitativa en tasa mientras la diferencia aparece ser la menos aparente con materiales compuestos. Las rupturas por fatiga de materiales compuestos puede formar en la matriz y propagarse lentamente ya que la matriz lleva tal fracción pequeña del esfuerzo aplicado. Y las fibras en la estela de la ruptura experimenta daño por fatiga. En muchos casos, la tasa de daño es acelerada por interacciones perjudiciales con el ambiente como oxidación o corrosión de fibras.
Fallas de fatiga notables
Choque de tren de Versalles


Siguiendo las celebraciones del rey Luis Felipe I en el Palacio de Versalles, un tren que retornaba a París, chocó en mayo de 1842, en Meudon, después que a la primera locomotora se le rompió un eje. Los carros de atrás se apilaron en los motores siniestrados y tomaron fuego. Al menos 55 pasajeros murieron atrapados en los carros cerrados, incluyendo al explorador Jules Dumont d'Urville. Este accidente es conocido en Francia como la "Catastrophe ferroviaire de Meudon". El accidente fue atestiguado por el ingeniero de locomotoras británico Joseph Locke y ampliamente reportado en Gran Bretaña. Fue discutido extensamente por ingenieros, quienes vieron una explicación.
El descarrilamiento había sido el resultado de un eje de locomotora roto. La investigación de Rankine de ejes rotos en Gran Bretaña, resaltó la importancia de la concentración de esfuerzos, y el mecanismo del crecimiento de ruptura con cargas repetidas. Sus y otros artículos sugirieron un mecanismo de crecimiento de ruptura por esfuerzos repetidos, sin embargo, fueron ignorados, y la falla de fatiga ocurrió a una tasa siempre incrementada en el sistema de ferrocarriles en expansión. Otras teorías espurreas parecen ser más aceptables, tales como la idea que el metal se había, de alguna manera, "cristalizado". La noción estaba basada en la apariencia cristalina en la región de ruptura rápida en la superficie de ruptura, pero ignoraba el hecho que el metal estaba ya altamente cristalizado.
El De Havilland Comet

Dos aviones de reacción de pasajeros De Havilland Comet se rompieron en vuelo y se estrellaron en unos pocos meses, uno del otro en 1954. Como resultado, pruebas sistemáticas fueron conducidas en un fuselaje inmerso y presurizado en un tanque de agua. Después de 3,000 vuelos equivalentes, los investigadores en el "Royal Aircraft Establishment (RAE)" fueron capaces de concluir que el siniestro había sido debido a falla de la cabina de presión en la ventana frontal de Radiogoniometría en el techo. Esta "ventana" fue, de hecho, una de dos aberturas para la antena de un sistema de navegación electrónica en el cual paneles de fibra de vidrio opaco tomaban el lugar de las ventanas de vidrio. La falla fue un resultado de fatiga de metal causada por la repetida presurización y despresurización de la cabina del avión. También, los soportes alrededor de la ventana estaban remachados, no soldados, tal como las especificaciones originales para el avión habían sugerido. El problema fue exacerbado por el empleo de la técnica de construcción de punzado de remaches. A diferencia, del taladrado para remaches, la naturaleza imperfecta del agujero creado al punzar los remaches causó rupturas de defecto de fabricación, las cuales pudieron causar el inicio de rupturas de fatiga alrededor del remache.

La presión de cabina del Comet había sido diseñada para un factor de seguridad cómodamente en exceso de aquel requerido por la "British Civil Airworthiness Requirements" (2.5 veces la presión de prueba (ing. proof test) de la cabina como opuesto al requerimiento de 1.33 veces y una carga última de 2.0 veces la presión de la cabina) y el accidente causó una revisión en los estimados de requerimientos de fortaleza de carga de seguridad de las cabinas de presión de aviones de reacción.
En adición, fue descubierto que los esfuerzos alrededor de las aperturas de la cabina de presión eran considerablemente más altos que los que habían sido anticipados, especialmente, alrededor de los cortes de esquina aguda, tales como las ventanas. Como resultado, todo avión de reacción futuro llevaría ventanas con esquinas redondeadas, reduciendo grandemente la concentración de esfuerzos. Esta fue una notable característica distintiva de todos los modelos posteriores del Comet. Los investigadores de la RAE dijeron a una consulta pública que las esquinas agudas cerca de las aberturas de ventanas del Comet actuaban como sitios de inicio para las rupturas. El fuselaje del avión era, también, demasiado delgado, y rupturas de esfuerzos de fabricación estaban presentes en las esquinas.
Plataforma petrolera Alexander L. Kielland zozobrando
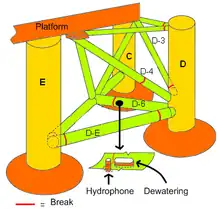
Alexander L. Kielland fue una plataforma petrolera semi sumergible noruega que zozobró mientras operaba en el yacimiento petrolero Ekofisk en marzo de 1980, matando 123 personas. La zozobra fue el peor desastre en aguas noruegas desde la II Guerra Mundial. La plataforma, localizada aproximadamente 320 km al este de Dundee, Escocia, era propiedad de la Stavanger Drilling Company de Noruega y estaba contratada por la compañía estadounidense Phillips Petroleum en el tiempo del desastre. En presencia de lluvia y niebla, temprano en la noche del 27 de marzo de 1980, más de 200 hombres estaban fuera de servicio en la acomodación en el Alexander L. Kielland. El viento estaba soplando a 40 nudos con olas arriba de 12 m de altura. La plataforma justo había sido soltada de la plataforma de producción Edda. Minutos antes a las 18:30, aquellos a bordo sintieron una "ruptura aguda" seguida por "alguna clase de temblor". Repentinamente, la plataforma se inclinó sobre 30° y luego se estabilizó. Cinco de los seis cables de anclaje se habían roto, con un cable remanente previniendo que la plataforma zozobrará. La escora continuo incrementándose y a las 18:53, el cable de anclaje remanente se rompió y la plataforma se torno boca abajo.
Un año después, en marzo de 1981, el reporte investigativo concluyó que la plataforma colapsó debido a una ruptura de fatiga en uno de los seis tirantes (tirante D-6), el conectaba la colapsada pierna D al resto de la plataforma. Esto fue rastreado a un pequeño filete de soldadura de 6 mm el cual unía una placa brida que no soportaba carga a este tirante D-6. Esta placa brida sujetaba un instrumento sonar durante las operaciones de taladrado. El pobre perfil del filete de soldadura contribuyó a la reducción en su fortaleza a la fatiga. Mas, la investigación encontró cantidades considerables de "lamellar tearing" en la placa brida y ruptura fría en las soldaduras, concentración de esfuerzos incrementadas debido a la placa brida debilitada, el pobre perfil de soldadura, y esfuerzos cíclicos (los cuales podrían ser comunes en el Mar del Norte), parecen jugar colectivamente un rol en el colapso de la plataforma.
Otros
| Año | Falla por fatiga |
|---|---|
| 1862 | Desastre Hartley Colliery fue causado por la fractura de un motor de vapor de viga y mató 204 personas |
| 1919 | La Gran inundación de melaza de Boston ha sido atribuida a falla por fatiga. |
| 1948 | Caída del Northwest Airlines Vuelo 421 debido a falla de fatiga en una raíz de spar de ala. |
| 1957 | Accidente de Cebu Douglas C-47 de 1957, el avión presidencial del Presidente filipino Ramón Magsaysay, se estrelló debido a falla de motor causada por fatiga de metal. |
| 1965 | Zozobra de la primera plataforma petrolera fuera de costa del RU, el Sea Gem, fue debido a fatiga en parte del sistema de suspensión vinculando el casco a las piernas. |
| 1968 | Los Angeles Airways Vuelo 417 perdió una de sus paletas de rotor principal debido a falla por fatiga. |
| 1968 | La MacRobertson Miller Airlines Vuelo 1750 perdió un ala debido a mantenimiento impropio que llevó a falla por fatiga. |
| 1969 | Caída del F-111A debido a falla por fatiga en el accesorio de pivote de ala de un defecto de material resultado en el desarrollo de la aproximación daño - tolerante para diseño de fatiga |
| 1977 | Caída del Dan-Air Boeing 707 causado por falla por fatiga resultando en la pérdida del estabilizador horizontal derecho. |
| 1979 | Vuelo 191 de American Airlines se estrelló después de la separación del motor atribuida a daño por fatiga en la estructura pilon que sujetaba el motor al ala, causado por procedimientos de mantenimiento impropios. |
| 1980 | Caída del Vuelo 7 de LOT debido a fatiga en árbol de motor de turbina resultando en la desintegración del motor que llevó a la pérdida de control. |
| 1985 | El Vuelo 123 de Japan Airlines se estrelló después que el avión perdió su estabilizador vertical debido a reparaciones defectuosas en el mamparo trasero. |
| 1988 | El Vuelo 243 de Aloha Airlines sufrió una descompresión explosiva a 24,000 pies (7,300 m) después de una falla por fatiga |
| 1989 | Vuelo 232 de United Airlines perdió su motor de cola debido a falla por fatiga en un cubo de disco de ventilador |
| 1992 | El Vuelo 1862 de El Al perdió ambos motores en su ala derecha debido a falla por fatiga en el pilón montante del motor #3. |
| 1998 | Accidente ferroviario de Eschede fue causado por falla por fatiga en una rueda de simple compuesto. |
| 2000 | El choque del Hatfield rail fue como causado por fatiga de contacto rodante. |
| 2000 | El rellamado de 6.5 millones de llantas Firestone de los Ford Explorers originado por crecimiento de ruptura por fatiga que llevaba a la separación de la huella de la llanta |
| 2002 | Vuelo 611 de China Airlines desintegrado en vuelo debido a falla por fatiga. |
| 2005 | Vuelo 101 de Chalk's Ocean Airways perdió su ala derecha debido a falla por fatiga traída por prácticas de mantenimiento inadecuadas. |
| 2009 | Descarrilamiento de tren Viareggio debido a falla por fatiga. |
| 2009 | Accidente de Estación de Potencia Sayano-Shushenskaya debido a fatiga de metal de soportes de turbina. |
| 2017 | Vuelo 66 de Air France tuvo en vuelo falla de motor debido fractura por fatiga en frío en el ventilador del cubo. |
Véase también
Referencias
- «High-Strength Reinforcing Steel Bars: Low Cycle Fatigue Behavior Using RGB Methodology». International Journal of Concrete Structures and Materials. Egger J.E., Rojas F.R., Massone L.M. 2021.
- Introducción a la Ciencia e Ingeniería de los Materiales William D. Callister