Fluido de Bingham
Un fluido de Bingham es un material viscoplástico que se comporta como un cuerpo rígido al estar sometido a tensiones reducidas pero fluye como un fluido viscoso al ejercer sobre el mismo tensiones mayores. Su designación hace referencia a Eugene C. Bingham quien propuso su formulación matemática.[1]

Se lo utiliza como un modelo frecuente para simular flujo de barro en ingeniería de perforaciones, y en la gestión de lodos líquidos. Un ejemplo común es la pasta dentífrica,[2] la cual no se extruda hasta que se aplica una determinada presión sobre el tubo. A partir de ese instante es empujada como un tapón coherente.
Explicación

La Figura 1 muestra un gráfico del comportamiento de un fluido viscoso (o newtoniano) ordinario en rojo, por ejemplo, en una tubería. Si se aumenta la presión en un extremo de una tubería, se produce una tensión en el fluido que tiende a hacer que se mueva (denominada tensión de corte) y el caudal volumétrico aumenta proporcionalmente. Sin embargo, para un fluido de Bingham (en azul), se puede aplicar tensión, pero no fluirá hasta que se alcance un cierto valor, la tensión de fluencia. Más allá de este punto, la tasa de flujo aumenta de manera constante al aumentar el esfuerzo cortante. Esta es aproximadamente la forma en que Bingham presentó su observación, en un estudio experimental de pinturas.[3] Estas propiedades le permiten al fluido de Bingham tener una superficie texturada con crestas y picos en vez de presentar una superficie lisa como la de un fluido newtoniano.
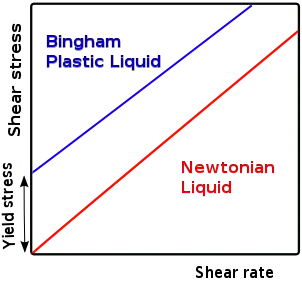
La Figura 2 muestra la forma en que se presenta el fluido de Bingham en la actualidad. [2] El gráfico muestra esfuerzo cortante en el eje vertical y velocidad cortante en el horizontal . (La tasa de flujo volumétrico depende del tamaño de la tubería, la tasa de corte es una medida de cómo cambia la velocidad con la distancia. Es proporcional a la tasa de flujo, pero no depende del tamaño de la tubería). Como antes, el fluido newtoniano fluye y da una tasa de corte para cualquier valor finito de esfuerzo cortante. Sin embargo, el fluido de Bingham nuevamente no exhibe ninguna tasa de cizallamiento (sin flujo y, por lo tanto, sin velocidad) hasta que se alcanza una cierta tensión. Para el fluido newtoniano, la pendiente de esta línea es la viscosidad, que es el único parámetro necesario para describir su flujo. Por el contrario, el fluido de Bingham requiere dos parámetros, el 'límite elástico' y la pendiente de la línea, conocida como 'viscosidad plástica' .
La razón física de este comportamiento es que el líquido contiene partículas (como arcilla) o moléculas grandes (como polímeros) que tienen algún tipo de interacción, creando una estructura sólida débil, antes conocida como cuerpo falso, y se requiere una cierta cantidad de tensión para romper esta estructura. Una vez que la estructura se ha roto, las partículas se mueven con el líquido bajo fuerzas viscosas. Si se elimina la tensión, las partículas se asocian nuevamente.
Definición
El material es un sólido elástico para una tensión de corte , menor que un valor crítico . Una vez que se excede la tensión de corte crítica (o "límite elástico"), el material fluye de tal manera que la velocidad de corte, ∂u/∂y (como se define en el artículo sobre viscosidad), es directamente proporcional a la cantidad por la cual la tensión de corte aplicado excede el límite elástico:
Fórmulas para el factor de fricción
En flujo de fluidos, un problema común es calcular la caída de presión en una red de tuberías.[4] Una vez que se conoce el factor de fricción, f, es más fácil manejar diferentes problemas de flujo de tuberías, a saber, calcular la caída de presión para evaluar la potencia de bombeo o para encontrar el caudal en una red de tuberías para una caída de presión determinada. Por lo general, es extremadamente difícil llegar a una solución analítica exacta para calcular el factor de fricción asociado con el flujo de fluidos no newtonianos y, por lo tanto, se utilizan aproximaciones explícitas para calcularlo. Una vez que se ha calculado el factor de fricción, la caída de presión se puede determinar fácilmente para un flujo dado mediante la ecuación de Darcy-Weisbach:
| Símbolo | Nombre | Unidad |
|---|---|---|
| Factor de fricción de Darcy | ||
| Caída de presión por fricción | m | |
| Longitud de la tubería | m | |
| Diámetro de la tubería | m | |
| Velocidad promedio del fluido | m/s | |
| Aceleración de la gravedad | m/s2 |
Flujo laminar
Una descripción exacta de la pérdida de fricción para fluidos de Bingham en un flujo laminar completamente desarrollado en una tubería fue desarrollado por Buckingham.[5] La expresión resultante, la ecuación de Buckingham–Reiner, en forma adimensional es la siguiente:
| Símbolo | Nombre | Unidad |
|---|---|---|
| Factor de fricción de Darcy para flujo laminar | ||
| Número de Reynolds | ||
| Número de Hedstrom |
El número de Reynolds y el número de Hedstrom se definen como:
| Símbolo | Nombre | Unidad |
|---|---|---|
| Número de Reynolds | ||
| Número de Hedstrom | ||
| Densidad del fluido | kg/m3 | |
| Viscosidad dinámica del fluido | kg / m s | |
| Límite elástico del fluido | Pa |
Flujo turbulento
Darby y Melson desarrollaron una expresión empírica[6] que luego fue refinada, y que queda expresada como:[7]
| Símbolo | Nombre | Unidad |
|---|---|---|
| Factor de fricción para flujo turbulento | ||
| Número de Reynolds | ||
| Símbolo | Nombre |
|---|---|
| Número de Hedstrom |
Nota: La expresión de Darby y Melson es para el factor de fricción de Fanning, y debe ser multiplicada por 4 para ser usada en las ecuaciones de pérdidas por fricción que se presentan en esta página.
Aproximaciones a la ecuación de Buckingham–Reinern
Si bien no es posible obtener una solución analítica exacta de la ecuación de Buckingham–Reiner porque es una ecuación polinómica de cuarto orden en f, a causa de la complejidad de la solución rara vez se utiliza. Por ello, los investigadores han desarrollado aproximaciones explícitas para la ecuación de Buckingham–Reiner.
Ecuación de Swamee–Aggarwal
La ecuación de Swamee–Aggarwal se utiliza para obtener de manera directa el factor de fricción f de Darcy–Weisbach para flujo laminar de fluidos de Bingham.[8] Es una aproximación de la ecuación implícita de Buckingham–Reiner, pero la discrepancia con los datos experimentales se encuentra dentro de la incerteza de dichos valores. The Swamee–Aggarwal equation is given by:
Solución de Danish–Kumar
Danish et al. han desarrollado un procedimiento explícito para calcular el factor de fricción f utilizando el método de descomposición de Adomian.[9] En este método el factor de fricción posee dos términos:
donde
y
Ecuación combinada del factor de fricción para todos los regímenes
Ecuación de Darby–Melson
En 1981, Darby y Melson, usando el modelo de Churchill[10] y de Churchill y Usagi,[11] desarrollaron una expresión para una sola ecuación del factor de fricción válida para todos los regímenes de flujo:[6]
donde:
Tanto la ecuación de Swamee–Aggarwal como la ecuación de Darby–Melson se pueden combinar para dar una ecuación explícita para determinar el factor de fricción para los fluidos de Bingham para todo régimen. La rugosidad relativa no es un parámetro en ninguna de las ecuaciones porque el factor de fricción de los fluidos de Bingham no es sensible a la rugosidad de la tubería.
Véase también
Referencias
- Bingham, E.C. (1916). «An Investigation of the Laws of Plastic Flow». Bulletin of the Bureau of Standards 13 (2): 309-353. doi:10.6028/bulletin.304.
- Steffe, J.F. (1996). Rheological Methods in Food Process Engineering (2nd edición). ISBN 0-9632036-1-4.
- Bingham, E.C. (1922). Fluidity and Plasticity. New York: McGraw-Hill. p. 219.
- Darby, Ron (1996). «Chapter 6». Chemical Engineering Fluid Mechanics. Marcel Dekker. ISBN 0-8247-0444-4.
- Buckingham, E. (1921). «On Plastic Flow Through Capillary Tubes». ASTM Proceedings 21: 1154-1156.
- Darby, R. and Melson J.(1981). "How to predict the friction factor for flow of Bingham plastics". Chemical Engineering 28: 59–61.
- Darby, R. (September 1992). «Prediction friction loss in slurry pipes». Chemical Engineering.
- Swamee, P.K. and Aggarwal, N.(2011). "Explicit equations for laminar flow of Bingham plastic fluids". Journal of Petroleum Science and Engineering. doi 10.1016/j.petrol.2011.01.015.
- Danish, M. et al. (1981). "Approximate explicit analytical expressions of friction factor for flow of Bingham fluids in smooth pipes using Adomian decomposition method". Communications in Nonlinear Science and Numerical Simulation 16: 239–251.
- Churchill, S.W. (7 de noviembre de 1977). «Friction factor equation spans all fluid-flow regimes». Chemical Engineering: 91-92.
- Churchill, S.W.; Usagi, R.A. (1972). «A general expression for the correlation of rates of transfer and other phenomena». AIChE Journal 18 (6): 1121-1128. doi:10.1002/aic.690180606.