Flujo Taylor-Couette

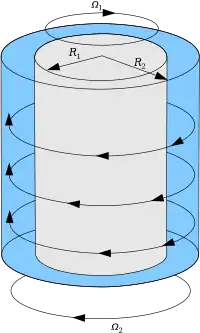
Un flujo Taylor-Couette simple es un flujo constante creado entre dos cilindros coaxiales rotativos infinitamente largos.[3] Dado que las longitudes de los cilindros son infinitamente largas, el flujo es esencialmente unidireccional en estado estable. Si el cilindro interior con radio ${\displaystyle R_{1}}$ gira a velocidad angular constante ${\displaystyle \Omega _{1}}$ y el cilindro exterior con radio ${\displaystyle R_{2}}$ gira a velocidad angular constante ${\displaystyle \Omega _{2}}$ como se muestra en la figura, entonces el componente de velocidad azimutal viene dado por:[4]

${\displaystyle v_{\theta }=Ar+{\frac {B}{r}},\quad A=\Omega _{1}{\frac {\mu -\eta ^{2}}{1-\eta ^{2}}},\quad B=\Omega _{1}R_{1}^{2}{\frac {1-\mu }{1-\eta ^{2}}}}$

${\displaystyle {\text{dónde}}\quad \mu ={\frac {\Omega _{2}}{\Omega _{1}}},\quad \eta ={\frac {R_{1}}{R_{2}}}}$.

Lord Rayleigh[6][7] estudió la estabilidad del problema con suposición no viscosa, es decir, perturbando las ecuaciones de Euler. El criterio establece que, en ausencia de viscosidad, la condición necesaria y suficiente para que la distribución de la velocidad azimutal ${\displaystyle v_{\theta }(r)}$ sea estable es

${\displaystyle {\frac {d}{dr}}(rv_{\theta })^{2}\geq 0}$

en todas partes en el intervalo; y, además, que la distribución es inestable si ${\displaystyle (rv_{\theta })^{2}}$ debería disminuir en cualquier parte del intervalo. Dado que ${\displaystyle |rv_{\theta }|}$ representa el momento angular por unidad de masa, de un elemento fluido alrededor del eje de rotación, una forma alternativa de establecer el criterio es: una estratificación del momento angular alrededor de un eje es estable si y solo aumenta monótonamente hacia afuera.

Líneas de corriente que muestran vórtices de Taylor-Couette en el plano radial-vertical, en Re = 950

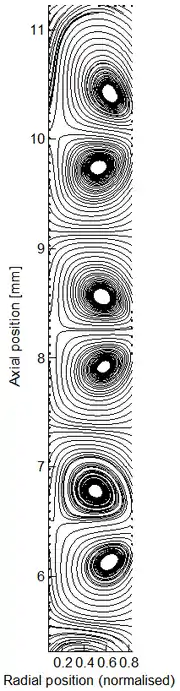
Los vórtices de Taylor (también llamados así en honor a Sir Geoffrey Ingram Taylor) son vórtices que se forman en el flujo rotativo de Taylor-Couette cuando el número de Taylor (${\displaystyle \mathrm {Ta} }$) del flujo excede un valor crítico ${\displaystyle \mathrm {Ta_{c}} }$.

Para flujo en el que

${\displaystyle \mathrm {Ta} <\mathrm {Ta_{c}} ,}$

no hay inestabilidades en el flujo, es decir, las perturbaciones del flujo se amortiguan mediante fuerzas viscosas y el flujo es constante. Pero, a medida que ${\displaystyle \mathrm {Ta} }$ supera ${\displaystyle \mathrm {Ta_{c}} }$, aparecen inestabilidades simétricas del eje. La naturaleza de estas inestabilidades es la de un intercambio de estabilidades (en lugar de una sobre estabilidad), y el resultado no es una turbulencia sino un patrón de flujo secundario estable que emerge en el que se forman grandes vórtices toroidales en el flujo, apilados uno encima del otro. Estos son los vórtices de Taylor. Si bien la mecánica de fluidos del flujo original es inestable cuando ${\displaystyle \mathrm {Ta} >\mathrm {Ta_{c}} }$, el nuevo flujo, llamado flujo de Taylor-Couette, con los vórtices de Taylor presentes, es en realidad estable hasta que el flujo alcanza un número de Reynolds grande, momento en el que el flujo pasa a un flujo de "vórtice ondulado" inestable, presumiblemente indicando la presencia de inestabilidades no simétricas.

El problema matemático idealizado se plantea eligiendo un valor particular de ${\displaystyle \mu }$, ${\displaystyle \eta }$, y ${\displaystyle \mathrm {Ta} }$. Como ${\displaystyle \eta \rightarrow 1}$ y ${\displaystyle \mu \rightarrow 1}$ desde abajo, el número crítico de Taylor es ${\displaystyle \mathrm {Ta_{c}} \simeq 1708}$[4][8][9][10][11]

En 1975, J. P. Gollub y H. L. Swinney publicaron un artículo sobre la aparición de turbulencias en un fluido en rotación. En un sistema de flujo Taylor-Couette, observaron que, a medida que aumenta la velocidad de rotación, el fluido se estratifica en una pila de "rosquillas fluidas". Con mayores aumentos en la tasa de rotación, las rosquillas oscilan y se retuercen y finalmente se vuelven turbulentas.[12] Su estudio ayudó a establecer el escenario de Ruelle-Takens en turbulencia,[13] que es una contribución importante de Floris Takens y David Ruelle para comprender cómo los sistemas hidrodinámicos pasan de patrones de flujo estables a turbulentos. Si bien el factor principal que rige esta transición es el número de Reynolds, existen otros factores de influencia importantes: si el flujo está abierto (lo que significa que hay un lateral ascendente y descendente) o cerrado (el flujo está lateralmente ligado; por ejemplo, giratorio), y delimitado (influenciado por efectos de pared) o ilimitado (no influenciado por efectos de pared). Según esta clasificación, el flujo de Taylor-Couette es un ejemplo de un patrón de flujo que se forma en un sistema de flujo cerrado y acotado.

• Wikimedia Commons alberga una categoría multimedia sobre Taylor–Couette flow.
• Chossat, P.; Iooss, G. (1992). El problema de Couette-Taylor. Ciencias Matemáticas Aplicadas 102. Springer. 102. Springer. ISBN 978-0387941547. doi:10.1007/978-1-4612-4300-7.
• Koschmieder, E. L. (1993). Células de Bénard y Vórtices de Taylor. Prensa de la Universidad de Cambridge. ISBN 978-0-521-40204-0.