Flujo no viscoso

Se denomina flujo no viscoso al flujo de un fluido sin viscosidad, en el cual la viscosidad del fluido es igual a cero.[1] Aunque hay ejemplos limitados de fluidos carentes de viscosidad, denominados superfluidos, el flujo no viscoso tiene muchas aplicaciones en la dinámica de fluidos.[1][2] El número de Reynolds del flujo no viscoso se aproxima a infinito a medida que la viscosidad tiende a cero.[1] Cuando se desprecian las fuerzas viscosas, como en el caso del flujo no viscoso, la ecuación de Navier-Stokes se puede simplificar a una forma denominada ecuación de Euler.[1] Esta ecuación simplificada es aplicable al flujo no viscoso así como a flujo con baja viscosidad y un número de Reynolds mucho mayor que uno.[1] Usando la ecuación de Euler, muchos problemas de dinámica de fluidos que involucran baja viscosidad se resuelven fácilmente, sin embargo, la viscosidad despreciable asumida ya no es válida en la región de fluido cerca de un determinado límite sólido..[3][1][4]

No es preciso que el fluido en sí tenga una viscosidad nula para que ocurra un flujo no viscoso. También es posible organizar el flujo de un fluido viscoso de forma tal que las fuerzas viscosas desaparezcan.[5] Tal flujo carece de resistencia viscosa a su movimiento. Estos "casos de flujo no viscoso" son de tipo vórtice y pueden desempeñar un papel clave en la formación de tornados, ciclones tropicales y la turbulencia.

Superfluidos

Helio superfluido.

Superfluido es el estado de la materia que exhibe flujo sin fricción, viscosidad cero, también conocido como flujo no viscoso.[2]

Hasta la fecha, el helio es el único fluido descubierto que exhibe superfluidez. El helio se convierte en un superfluido una vez que se enfría por debajo de 2.2K, un punto denominado punto lambda.[6] A temperaturas superiores al punto lambda, el helio existe como un líquido que exhibe un comportamiento dinámico de fluido normal. Una vez que se enfría por debajo de 2.2K, comienza a exhibir un comportamiento cuántico. Por ejemplo, en el punto lambda hay un fuerte aumento en la capacidad de calor, y si se le continúa enfriando, la capacidad de calor comienza a disminuir con la temperatura.[7] Además, la conductividad térmica es muy grande, lo que contribuye a las excelentes propiedades como refrigerante del helio superfluido.[8]

Número de Reynolds

El número de Reynolds (Re) es una cantidad adimensional que se usa comúnmente en dinámica de fluidos e ingeniería.[9][10] Originalmente descrito por George Gabriel Stokes en 1850, Osborne Reynolds le dio popularidad, después de que el concepto fue nombrado por Arnold Sommerfeld en 1908.[10][11][12] El número de Reynolds se calcula como:

$Re={l_{c}v\rho \over \mu }$

Símbolo	Descripción	Unidades
$l_{c}$	longitud característica	m
$v$	velocidad del fluido	m/s
$\rho$	densidad del fluido	kg/m³
$\mu$	viscosidad del fluido	Pa*s

El valor representa la relación entre las fuerzas inerciales y las fuerzas viscosas en un fluido, y es útil para determinar la importancia relativa de la viscosidad.[9] En un flujo no viscoso, dado que las fuerzas viscosas son nulas, el número de Reynolds tiende a infinito.[1] Cuando las fuerzas viscosas son despreciables, el número de Reynolds es mucho mayor que uno.[1] En tales casos (Re>>1), suponer un flujo no viscoso puede permitir simplificar muchos problemas de dinámica de fluidos.

Ecuaciones de Euler

Este tipo de problema de dinámica de los fluidos puede ser descrito mediante la ecuación de Euler.

Flujo no viscoso alrededor de un ala, suponiendo una circulación que satisface una condición de Kutta

En un escrito publicado en 1757, Leonhard Euler describió un conjunto de ecuaciones que se aplican a un flujo no viscoso:[13]

$\rho {D\mathbf {v} \over Dt}=-\nabla p+\rho \mathbf {g}$

Símbolo	Descripción	Unidades
${D \over Dt}$	derivada material
$\nabla$	operador nabla
$p$	presión	Pa
$\mathbf {g}$	vector aceleración de gravedad	m/s²

Assuming inviscid flow allows the Euler equation to be applied to flows in which viscous forces are insignificant.[1] Some examples include flow around an airplane wing, upstream flow around bridge supports in a river, and ocean currents.[1]

Ecuaciones de Navier-Stokes

En 1845, George Gabriel Stokes publicó otro conjunto importante de ecuaciones, hoy conocidas como las ecuaciones de Navier-Stokes.[1][14] Claude-Louis Navier desarrolló las ecuaciones primero usando la teoría molecular, lo que Stokes confirmó usando la teoría del continuo.[1] Las ecuaciones de Navier-Stokes describen el movimiento de los fluidos:[1]

$\rho {D\mathbf {v} \over Dt}=-\nabla p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {g}$

Cuando el fluido es no viscoso, o cuando se asume que la viscosidad es despreciable, la ecuación de Navier-Stokes se simplifica y resulta la ecuación de Euler:[1] Esta simplificación es mucho más fácil de resolver, y se puede aplicar a muchos tipos de flujo en que la viscosidad puede ser despreciada.[1] Algunos ejemplos son el flujo que rodea un ala de un avión, el flujo alrededor de los soportes hincados en el río que sostienen un puente, y las corrientes oceánicas.[1]

La ecuación de Navier-Stokes se reduce a la ecuación de Euler cuando $\mu =0$ . Otra condición que conduce a la eliminación de la fuerza viscosa es $\nabla ^{2}\mathbf {v} =0$ , y ello resulta en una "disposición de flujo no viscoso".[5] Tales flujos son de tipo vórtice.

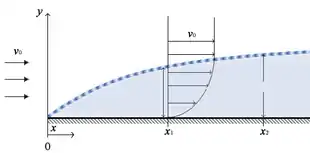
Flow far from the solid interface, viscosity is largely unimportant

Flujo desarrollándose sobre una interfase sólida.

Fronteras sólidas

Es importante tener en cuenta que no se puede suponer una viscosidad insignificante cerca de fronteras sólidas, como el caso del ala de un avión.[1] En los regímenes de flujo turbulento (Re >> 1), la viscosidad generalmente puede descartarse, sin embargo, esto solo es válido a distancias lejos de interfaces sólidas.[1] Al considerar el flujo en la vecindad de una superficie sólida, como el flujo a través de una tubería o alrededor de un ala, es conveniente clasificar cuatro regiones distintas de flujo cerca de la superficie:[1]

Corriente turbulenta principal: la más lejana de la superficie, allí se puede despreciar la viscosidad.
Subcapa inercial: zona donde se inicia la corriente turbulenta principal, en ella la viscosidad tiene una importancia menor.
Capa de amortiguación: la zona de transformación entre capas inerciales y viscosas.
Subcapa viscosa: la zona más cercana a la superficie, aquí la viscosidad es importante.

Aunque estas distinciones pueden ser una herramienta útil para ilustrar la importancia de las fuerzas viscosas cerca de interfaces sólidas, es importante tener en cuenta que estas regiones son bastante arbitrarias.[1] Sin embargo, considerando que el flujo no viscoso puede ser una herramienta útil para resolver muchos problemas de dinámica de fluidos, este supuesto requiere una cuidadosa consideración de las subcapas de fluidos cuando están involucradas fronteras sólidas.

Véase también

Flujo de Couette
Dinámica de fluidos
Flujo potencial, un caso especial de flujo no viscoso
Flujo de Stokes, en el cual las fuerzas viscosas son mucho mayores que las fuerzas inerciales.
Viscosidad

Referencias

E., Stewart, Warren; N., Lightfoot, Edwin (1 de enero de 2007). Transport phenomena. Wiley. ISBN 9780470115398. OCLC 762715172.
S., Stringari (2016). Bose-Einstein condensation and superfluidity. ISBN 9780198758884. OCLC 936040211.
Clancy, L.J., Aerodynamics, p.xviii
Kundu, P.K., Cohen, I.M., & Hu, H.H., Fluid Mechanics, Chapter 10, sub-chapter 1
Runstedtler, Allan (2013). «Inviscid Flow Arrangements in Fluid Dynamics». International Journal of Fluid Mechanics Research (en inglés) 40 (2): 148-158. ISSN 1064-2277. doi:10.1615/interjfluidmechres.v40.i2.50.
«This Month in Physics History». www.aps.org (en inglés). Consultado el 7 de marzo de 2017.
Landau, L. (1941). «Theory of the Superfluidity of Helium II». Physical Review 60 (4): 356-358. Bibcode:1941PhRv...60..356L. doi:10.1103/physrev.60.356.
«nature physics portal - looking back - Going with the flow -- superfluidity observed». www.nature.com. Consultado el 7 de marzo de 2017.
L., Bergman, Theodore; S., Lavine, Adrienne; P., Incropera, Frank; P., Dewitt, David (1 de enero de 2011). Fundamentals of heat and mass transfer. Wiley. ISBN 9780470501979. OCLC 875769912.
Rott, N (28 de noviembre de 2003). «Note on the History of the Reynolds Number». Annual Review of Fluid Mechanics (en inglés) 22 (1): 1-12. Bibcode:1990AnRFM..22....1R. doi:10.1146/annurev.fl.22.010190.000245.
Reynolds, Osborne (1 de enero de 1883). «An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels». Philosophical Transactions of the Royal Society of London (en inglés) 174: 935-982. Bibcode:1883RSPT..174..935R. ISSN 0261-0523. doi:10.1098/rstl.1883.0029.
Stokes, G. G. (1 de enero de 1851). «On the Effect of the Internal Friction of Fluids on the Motion of Pendulums». Transactions of the Cambridge Philosophical Society 9: 8. Bibcode:1851TCaPS...9....8S.
Euler, Leonhard (1757). «"Principes généraux de l'état d'équilibre d'un fluide" [General principles of the state of equilibrium]». Mémoires de l'académie des sciences de Berlin 11: 217-273.
Stokes, G. G. (1845). «On the Theories of the Internal Friction of Fluids in Motion and of the Equilibrium and Motion of Elastic Solids.». Proc. Camb. Phil. Soc. 8: 287-319.

Datos: Q2247765

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[:03-1] E., Stewart, Warren; N., Lightfoot, Edwin (1 de enero de 2007). Transport phenomena. Wiley. ISBN 9780470115398. OCLC 762715172.

[:0-2] S., Stringari (2016). Bose-Einstein condensation and superfluidity. ISBN 9780198758884. OCLC 936040211.

[3] Clancy, L.J., Aerodynamics, p.xviii

[4] Kundu, P.K., Cohen, I.M., & Hu, H.H., Fluid Mechanics, Chapter 10, sub-chapter 1

[:4-5] Runstedtler, Allan (2013). «Inviscid Flow Arrangements in Fluid Dynamics». International Journal of Fluid Mechanics Research (en inglés) 40 (2): 148-158. ISSN 1064-2277. doi:10.1615/interjfluidmechres.v40.i2.50.

[6] «This Month in Physics History». www.aps.org (en inglés). Consultado el 7 de marzo de 2017.

[7] Landau, L. (1941). «Theory of the Superfluidity of Helium II». Physical Review 60 (4): 356-358. Bibcode:1941PhRv...60..356L. doi:10.1103/physrev.60.356.

[8] «nature physics portal - looking back - Going with the flow -- superfluidity observed». www.nature.com. Consultado el 7 de marzo de 2017.

[:2-9] L., Bergman, Theodore; S., Lavine, Adrienne; P., Incropera, Frank; P., Dewitt, David (1 de enero de 2011). Fundamentals of heat and mass transfer. Wiley. ISBN 9780470501979. OCLC 875769912.

[:3-10] Rott, N (28 de noviembre de 2003). «Note on the History of the Reynolds Number». Annual Review of Fluid Mechanics (en inglés) 22 (1): 1-12. Bibcode:1990AnRFM..22....1R. doi:10.1146/annurev.fl.22.010190.000245.

[:1-11] Reynolds, Osborne (1 de enero de 1883). «An Experimental Investigation of the Circumstances Which Determine Whether the Motion of Water Shall Be Direct or Sinuous, and of the Law of Resistance in Parallel Channels». Philosophical Transactions of the Royal Society of London (en inglés) 174: 935-982. Bibcode:1883RSPT..174..935R. ISSN 0261-0523. doi:10.1098/rstl.1883.0029.

[12] Stokes, G. G. (1 de enero de 1851). «On the Effect of the Internal Friction of Fluids on the Motion of Pendulums». Transactions of the Cambridge Philosophical Society 9: 8. Bibcode:1851TCaPS...9....8S.

[13] Euler, Leonhard (1757). «"Principes généraux de l'état d'équilibre d'un fluide" [General principles of the state of equilibrium]». Mémoires de l'académie des sciences de Berlin 11: 217-273.

[14] Stokes, G. G. (1845). «On the Theories of the Internal Friction of Fluids in Motion and of the Equilibrium and Motion of Elastic Solids.». Proc. Camb. Phil. Soc. 8: 287-319.