Función de Liapunov
En matemática, las funciones de Liapunov, planteadas principalmente por el ruso Aleksandr Liapunov, son funciones que demuestran la estabilidad de cierto punto fijo en un sistema dinámico o en las ecuaciones diferenciales autónomas. Las funciones que podrían probar la estabilidad de un punto cualquiera de equilibrio son llamadas candidatas a funciones de Liapunov.
No existe un método general para construir o encontrar una función candidata de Liapunov que demuestre la estabilidad de un equilibrio dado, en todo caso, la incapacidad de encontrar una función de Liapunov no implica automáticamente la inestabilidad del equilibrio mismo. Para los sistemas dinámicos (como los sistemas físicos) las leyes de conservación proveen frecuentemente a las funciones candidatas de Liapunov.
El segundo teorema de estabilidad de Liapunov para los sistemas autónomos los hace estrechamente correlativos con las funciones candidatas de Liapunov y son instrumentos para demostrar la estabilidad de los equilibrios de un sistema dinámico autónomo.
Es menester saber que el segundo teorema de estabilidad de Liapunov para los sistemas autónomos aporta condiciones suficientes pero no necesarias para demostrar la estabilidad de un equilibrio.
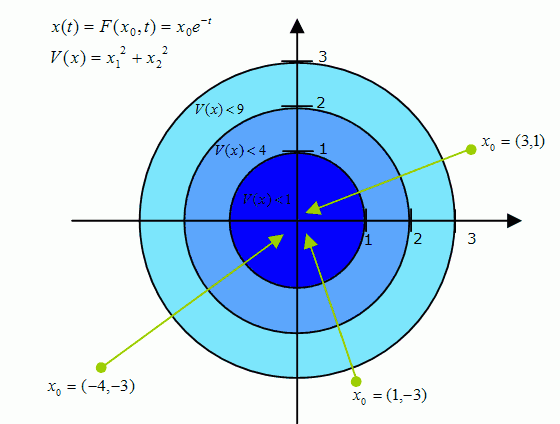
Definición intuitiva de una función de Liapunov
Un sistema dinámico requiere un estado inicial y una función de evolución que indica la trayectoria de los estados futuros que tendrá el sistema. Una función de Liapunov corresponde intuitivamente a una familia de regiones de Liapunov, cada una de las cuales queda definida por una curva de nivel. Una vez que el estado ha entrado a la región de Liapunov correspondiente a la curva de nivel , ya no podrá salir de ella. De este modo, a medida que el tiempo avanza, el estado irá quedando restringido a regiones de Liapunov cada vez menores, razón por la cual el valor de la función de Liapunov irá decreciendo al pasar el tiempo. La restricción en las trayectorias que imponen las curvas de nivel permiten asegurar que el sistema dinámico es estable.
Definición de una función candidata de Liapunov
Sea
una función escalar. y dicha función candidata de Liapunov si es localmente (en 0) una función definida positiva o, equivalentemente, si existe un entorno de 0 tal que
Teorema de Estabilidad de Liapunov
Sea
un punto de equilibrio del sistema autónomo
y sea
la derivada respecto al tiempo de una función candidata de Liapunov .
Equilibrio estable
Si la derivada respecto al tiempo de (la función candidata de Liapunov) está localmente semidefinida negativa, entonces existe un entorno centrado en 0 tal que
entonces el equilibrio es estable, para algún entorno o vecindad .
Equilibrio localmente atractivo
Si la derivada respecto al tiempo de la función candidata de Liapunov está localmente definida negativa, esto es si existe un entorno de 0 tal que:
entonces el equilibrio es localmente atractivo.
Equilibrio globalmente atractivo
Si las funciones candidatas de Liapunov están definidas como positiva sobre todo el dominio y si su derivada respecto al tiempo es globalmente definida como negativa, esto es
entonces el equilibrio es globalmente atractivo.
Bibliografía
- Alessandro Giua, Carla Seatzu (2006). Analisi dei sistemi dinamici. Springer. ISBN:978-88-470-0284-5.