Punto de equilibrio

El punto ${\displaystyle {\tilde {\mathbf {x} }}\in \mathbb {R} ^{n}}$ es un punto de equilibrio para la ecuación diferencial

${\displaystyle {\frac {d\mathbf {x} }{dt}}=\mathbf {f} (t,\mathbf {x} )}$

Si ${\displaystyle \mathbf {f} (t,{\tilde {\mathbf {x} }})=\mathbf {0} }$ para todos ${\displaystyle t}$

Del mismo modo, el punto ${\displaystyle {\tilde {\mathbf {x} }}\in \mathbb {R} ^{n}}$ es un punto de equilibrio (o punto fijo) para la ecuación en diferencias

${\textstyle \mathbf {x} _{k+1}=\mathbf {f} (k,\mathbf {x} _{k})}$

Si ${\displaystyle \mathbf {f} (k,{\tilde {\mathbf {x} }})={\tilde {\mathbf {x} }}}$ para ${\displaystyle k=0,1,2,\ldots }$

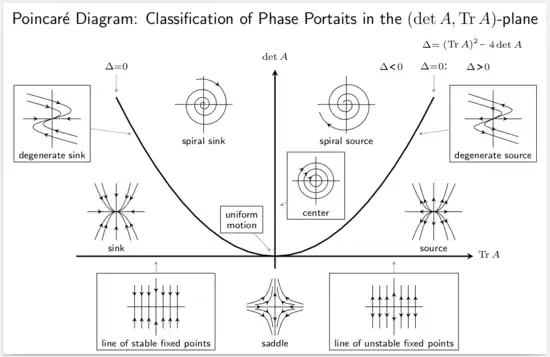
Los equilibrios pueden clasificarse observando los signos de los valores propios de la linealización de las ecuaciones sobre los equilibrios. Es decir, evaluando la matriz jacobiana en cada uno de los puntos de equilibrio del sistema, y luego encontrando los valores propios resultantes, los equilibrios se pueden categorizar. Entonces, el comportamiento del sistema en la vecindad de cada punto de equilibrio puede determinarse cualitativamente (o incluso determinarse cuantitativamente, en algunos casos), encontrando los vectores propios asociados con cada valor propio.

Un punto de equilibrio es hiperbólico si ninguno de los valores propios tiene una parte real cero. Si todos los valores propios tienen una parte real negativa, el equilibrio es una ecuación estable. Si al menos uno tiene una parte real positiva, el equilibrio es un nodo inestable. Si al menos un valor propio tiene una parte real negativa y al menos uno tiene una parte real positiva, el equilibrio es un punto de silla.

Diagrama de estabilidad clasificando mapas de Poincaré del sistema autónomo lineal ${\displaystyle x'=Ax,}$ como estables o inestables según sus características. La estabilidad generalmente aumenta a la izquierda del diagrama.[1] Algunos sumideros, fuentes o nodos son puntos de equilibrio.

• Punto crítico
• Estado estable

• Boyce, William E.; DiPrima, Richard C. (2012). Elementary Differential Equations and Boundary Value Problems (10th edición). Wiley. ISBN 978-0-470-45831-0.
• Perko, Lawrence (2001). Differential Equations and Dynamical Systems (3rd edición). Springer. pp. 102-104. ISBN 1-4613-0003-7.