Función de distribución radial
En mecánica estadística, la función de distribución radial, (o función de correlación de pares) g(r), en un sistema de partículas (átomos, moléculas, coloides, etc.), describe la variación de la densidad como función de la distancia medida desde una partícula de referencia.
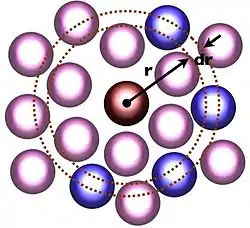
Si se toma una partícula dada como ubicada en el origen O, y si ρ = N/V es la densidad numérica promedio, entonces la densidad local promediada en el tiempo a una distancia r desde O es ρg(r). Esta definición simplificada es válida para un sistema isotrópico y homogéneo. Más adelante se considera un caso más general.
En términos más simples, es una medida de la probabilidad de encontrar una partícula a una distancia r desde una partícula de referencia dada, relativa a la de un gas ideal. El algoritmo general para el cálculo de g(r) involucra el determinar cuántas partículas se encuentran a una distancia r + dr de una partícula de referencia. Esto se muestra en la figura de la derecha, donde la partícula roja es la partícula de referencia y las partículas azules son la que se encuentran dentro de un cascarón esférico mostrado en anaranjado.
La función de distribución radial se determina usualmente calculando la distancia entre todos los pares de partículas y colocando los datos en un histograma. Entonces, el histograma se normaliza con respecto a un gas ideal completamente descorrelacionado. En tres dimensiones, esta normalización es la densidad numérica del sistema, multiplicada por el volumen del cascarón esférico; es decir:
donde ρ es la densidad numérica.
Dada una función de energía potencial, g(r) puede calcularse ya sea por medio de métodos numéricos como el método de Monte Carlo o a través de la ecuación de Ornstein-Zernike, utilizando relaciones de cerradura aproximadas como la aproximación de Percus-Yevick o la teoría de cadena hipertejida. También puede determinarse experimentalmente por medio de técnicas de dispersión de radiación o a través de la visualización directa para partículas lo suficientemente grandes (del tamaño de micras), por medio de microscopia tradicional o confocal.
La función de distribución radial es de particular importancia en la termodinámica, ya que las cantidades termodinámicas macroscópicas pueden determinarse usualmente a través de g(r).

Definición
Considérese un sistema de N partículas en un volumen V (para una densidad numérica promedio ρ = N/V) a una temperatura T. Definamos también el parámetro β = 1/(kT), donde k es la constante de Boltzmann. Las coordenadas de las partículas son ri , con i = 1,…,N. La energía potencial debida a la interacción entre las partículas es UN(r1,…,rN) y no consideramos el caso de un campo aplicado externamente.
Los promedios apropiados se toman en el ensamble canónico (N,V,T) con la integral configuracional sobre todos las posibles combinaciones de posiciones de partículas:
- .
La probabilidad de encontrar a la partícula 1 en el intervalo dr1, a la partícula 2 en dr2, etc. está dada por
(1).
Dado que el número de partículas es muy grande, P(N) no es muy útil por sí mismo. No obstante, se puede obtener al probabilidad de una configuración reducida, donde las posiciones de únicamente n < N partículas están fijas en r1,…,rn , sin restricciones sobre las N−n partículas restantes. Hasta este punto, es necesario integrar () sobre las coordenadas restantes rn+1,…,rN :
- .
Ya que las partículas son idénticas, es más relevante considerar la probabilidad de que cualesquiera n de ellas ocupen las posiciones r1,…,rn , en cualquier permutación, definiendo así la densidad de n partículas:
(2).
Para n = 1, () da la densidad de 1 partícula, la cual, para un cristal es una función periódica con máximos puntiagudos en los sitios de la red. Para un líquido homogéneo, es independiente de la posición r1 y es igual a la densidad total del sistema:
- .
Introducimos ahora la función de correlación g(n) a través de
(3).
La función g(n) es conocida como función de correlación, dado que, si los átomos son independientes unos de otros, ρ(n) sería simplemente igual a ρn. Entonces, g(n) corrige la correlación entre átomos.
A partir de () y de () se obtiene que
(4).
Relaciones que involucran g(r)
Factor de estructura
La función de correlación de segundo orden g(2)(r1,r2) es especialmente importante, ya que está relacionada (a través de la transformada de Fourier) con el factor de estructura del sistema.
Si el sistema consiste de partículas esféricamente simétricas, g(2)(r1,r2) depende únicamente de la distancia relativa entre ellas, r12 = r2−r1. Quitando los subíndices y los superíndices escribimos: g(r) ≡ g(2)(r12). Si tomamos a la partícula 0 como fija en el origen de coordenadas, ρg(r) dr = dn(r) es el número de partículas (entre las N−1 restantes) que se encuentran en el volumen dr alrededor de la posición r.
Formalmente, podemos contar estas partículas como
donde los paréntesis angulares, 〈 〉, indican el promedio sobre el ensamble, lo que da
La segunda igualdad requiere la equivalencia de partículas 1,…,N−1. La fórmula anterior es útil para relacionar g(r) con el factor de estructura estático S(q), definido como
Los términos para los que i = j, suman en total una unidad, por lo que se puede escribir
Usando las propiedades de la delta de Dirac tenemos de la ecuación anterior que
y, por lo tanto,
(5)
lo que prueba la relación de Fourier mencionada anteriormente.
Esta ecuación es válida solamente en el sentido de distribuciones. Puesto que g(r) no está normalizada,
- ,
así que ∫V g(r) dr diverge con el volumen V, lo que implica una delta de Dirac en el origen para el factor de estructura. Ya que esta información no es accesible experimentalmente, se puede sustraer de la ecuación y redefinir el factor de estructura como una función regular:
- .
Finalmente, podemos renombrar S(q) ≡ S′(q) y, si el sistema es un líquido, podemos invocar su isotropía:
(6).
Ecuación de compresibilidad
Evaluando () en q = 0 y usando la relación entre la compresibilidad isotérmica χT y el factor de estructura en el origen, se obtiene la ecuación de compresibilidad:
(7).
Potencial de fuerza media
Se puede demostrar[1] que la función de distribución radial está relacionada con el potencial de fuerza media para dos partículas, w(2)(r), a través de:
(8).
Ecuación de energía
Si las partículas interaccionan a través de potenciales a pares idénticos,
- ,
la energía interna promedio por partícula es:[2]: Sección 2.5
(9).
Ecuación de estado para la presión
Desarrollando la ecuación de estado del virial se obtiene la ecuación de estado para la presión:
(10).
Propiedades termodinámicas
La función de distribución radial es una medida importante ya que, a partir de ella se pueden calcular varias propiedades termodinámicas clave.
Para sistemas tridimensionales, en donde las partículas interaccionan a través de potenciales por pares, la energía potencial del sistema puede calcularse de la siguiente manera:[3]
donde N es el número de partículas del sistema, ρ es la densidad numérica y u(r) es el potencial a pares.
También puede calcularse la presión del sistema si se relaciona el segundo coeficiente del virial con g(r). Esto se hace de la siguiente manera:[3]
donde T es la temperatura y kB es la constante de Boltzmann. Nótese que los resultados para la energía potencial y la presión no serán lo suficientemente precisos, comparados con cómo serían al calcularlos directamente, debido al promedio que se requiere en el cálculo de g(r).
Aproximaciones
En sistemas diluidos (por ejemplo, los gases), las correlaciones de las posiciones de las partículas expresadas por g(r) se deben únicamente al potencial u(r) generado por la partícula de referencia, ignorando los efectos indirectos. Como primera aproximación, la correlación está dada simplemente por la ley de distribución de Boltzmann:
(11)
Si u(r) fuese cero para toda r —es decir, si las partículas no ejerciesen ninguna influencia entre ellas—, entonces g(r) = 1 para toda r y la densidad media local sería igual a la densidad media ρ. La presencia de una partícula en O no afectaría la distribución de partículas alrededor de ella y el gas sería ideal. En distancias r para las que u(r) es significativa, la densidad media local diferirá de la densidad media ρ, dependiendo del signo de u(r) (será mayor para interacciones negativas y menor para potenciales positivos).
Conforme la densidad del gas se incrementa, el límite de baja densidad deja de ser preciso, puesto que una partícula localizada en r experimenta no solamente la interacción con la partícula en O, sino también con sus vecinas, las cuales se encuentran también bajo la influencia de la partícula de referencia. Esta interacción mediada se incrementa con la densidad, puesto que habrá más vecinas con las cuales interaccionar. Tiene sentido entonces escribir una expansión de g(r) en términos de ρ, semejante a la ecuación del virial:
(12).
Esta similitud no es accidental; de hecho, al sustituir () en las relaciones anteriores de los parámetros termodinámicos —ecuaciones (), () y ()—, se obtienen las expansiones del virial correspondientes.[4] La función auxiliar y(r) se conoce como función de distribución de cavidades.[2]: Tabla 4.1
Obtención experimental
Se puede determinar g(r) indirectamente —a través de su relación con el factor de estructura S(q)— usando datos obtenidos a por medio de dispersión de neutrones o dispersión de rayos X. La técnica puede ser usada en escalas de longitud bastante cortas (hasta niveles atómicos[5]), pero implica promediar significativamente en espacio y tiempo (sobre el tamaño de la muestra y el tiempo de adquisición, respectivamente). De esta forma, la función de distribución radial puede determinarse para una gran variedad de sistemas, desde los metales líquidos[6] hasta los coloides cargados.[7] Nótese que ir desde la función S(q) experimental hasta g(r) no es directo y se requiere gran cantidad de análisis.[8]
Es posible calcular g(r) directamente obteniendo las posiciones de las partículas a partir de microscopia tradicional o confocal.[9] Esta técnica está limitada a partículas lo suficientemente grandes para ser detectadas ópticamente (en el rango de micras), pero tiene como ventaja que tiene resolución temporal. Por lo tanto, además de la información estática, permite tener acceso a los parámetros dinámicos (por ejemplo, las constantes de difusión[10]). Asimismo, este tipo de obtención tiene resolución espacial (al nivel de partículas individuales), lo que permite revelar la morfología[11] y la dinámica de las estructuras locales en cristales coloidales,[12] vidrios,[13] geles,[14][15] y las interacciones hidrodinámicas.[16]
Funciones de correlación de orden superior
Las funciones de correlación de orden superior, g(k), con k > 2, han sido menos estudiadas, puesto que generalmente son menos importantes para la termodinámica del sistema; además, no son accesibles con técnicas de dispersión convencionales. Sin embargo, estas funciones pueden ser medidas a través de dispersión de rayos X coherente y son interesantes puesto que revelan las simetrías locales en sistemas desordenados.[17]
Referencias
- Chandler, D. (1987). «Sección 7.3». Introduction to Modern Statistical Mechanics. Oxford University Press.
- Hansen, J. P. y McDonald, I. R. (2005). Theory of Simple Liquids (3.ª edición). Academic Press.
- Smit, D. F. B. (2002). Understanding molecular simulation from algorithms to applications (2.ª edición). San Diego: Academic Press. ISBN 0122673514.
- Barker, J. y Henderson, (1976). «What is a “liquid”? Understanding the states of matter». Review of Modern Physics 48 (4): 587.
- Yarnell, J.; Katz, M.; Wenzel, R.; Koenig, S. (1973). «Structure Factor and Radial Distribution Function for Liquid Argon at 85 K». Physical Review A 7 (6): 2130. doi:10.1103/PhysRevA.7.2130.
- Gingrich, N. S.; Heaton, L. (1961). «Structure of Alkali Metals in the Liquid State». The publicación of Chemical Physics 34 (3): 873. doi:10.1063/1.1731688.
- Sirota, E.; Ou-Yang, H.; Sinha, S.; Chaikin, P.; Axe, J.; Fujii, Y. (1989). «Complete phase diagram of a charged colloidal system: A synchrotron x-ray scattering study». Physical Review Letters 62 (13): 1524-1527. doi:10.1103/PhysRevLett.62.1524.
- Pedersen, J. S. (1997). «Analysis of small-angle scattering data from colloids and polymer solutions: Modeling and least-squares fitting». Advances in Colloid and Interface Science 70: 171-201. doi:10.1016/S0001-8686(97)00312-6.
- Crocker, J. C.; Grier, D. G. (1996). «Methods of Digital Video Microscopy for Colloidal Studies». Journal of Colloid and Interface Science 179: 298-201. doi:10.1006/jcis.1996.0217.
- Nakroshis, P.; Amoroso, M.; Legere, J.; Smith, C. (2003). «Measuring Boltzmann's constant using video microscopy of Brownian motion». American Journal of Physics 71 (6): 568. doi:10.1119/1.1542619.
- Pagnola, M. R.; Morales, F.; Tancredi, P.; Socolovsky, L. M. (1 de agosto de 2021). «Radial Distribution Function Analysis and Molecular Simulation of Graphene Nanoplatelets Obtained by Mechanical Ball Milling». JOM (en inglés) 73 (8): 2471-2478. ISSN 1543-1851. doi:10.1007/s11837-020-04499-5. Consultado el 24 de enero de 2022.
- Gasser, U.; Weeks, E. R.; Schofield, A.; Pusey, P. N.; Weitz, D. A. (2001). «Real-Space Imaging of Nucleation and Growth in Colloidal Crystallization». Science 292 (5515): 258-262. doi:10.1126/science.1058457.
- Weeks, E. R.; Crocker, J. C.; Levitt, A. C.; Schofield, A.; Weitz, D. A. (2000). «Three-Dimensional Direct Imaging of Structural Relaxation Near the Colloidal Glass Transition». Science 287 (5453): 627-631. PMID 10649991. doi:10.1126/science.287.5453.627.
- Cipelletti, L.; Manley, S.; Ball, R. C.; Weitz, D. A. (2000). «Universal Aging Features in the Restructuring of Fractal Colloidal Gels». Physical Review Letters 84 (10): 2275-2278. Bibcode:2000PhRvL..84.2275C. PMID 11017262. doi:10.1103/PhysRevLett.84.2275.
- Varadan, P.; Solomon, M. J. (2003). «Direct Visualization of Long-Range Heterogeneous Structure in Dense Colloidal Gels». Langmuir 19 (3): 509. doi:10.1021/la026303j.
- Gao, C.; Kulkarni, S. D.; Morris, J. F.; Gilchrist, J. F. (2010). «Direct investigation of anisotropic suspension structure in pressure-driven flow». Physical Review E 81 (4). Bibcode:2010PhRvE..81d1403G. doi:10.1103/PhysRevE.81.041403.
- Wochner, P.; Gutt, C.; Autenrieth, T.; Demmer, T.; Bugaev, V.; Ortiz, A. D.; Duri, A.; Zontone, F.; Grubel, G.; Dosch, H. (2009). «X-ray cross correlation analysis uncovers hidden local symmetries in disordered matter». Proceedings of the National Academy of Sciences 106 (28): 11511. doi:10.1073/pnas.0905337106.
Bibliografía
- Widom, B. (2002). Statistical Mechanics: A Concise Introduction for Chemists. Cambridge University Press.
- McQuarrie, D. A. (1976). Statistical Mechanics. Harper Collins Publishers.
Enlaces externos
- Esta obra contiene una traducción derivada de «Radial distribution function» de Wikipedia en inglés, concretamente de esta versión del 23 de mayo de 2014, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.