Gömböc
Un gömböc o gomboc("Gómboco" en español[cita requerida] (Pronunciación en húngaro: /ˈɡømbøt͡s/) es un cuerpo convexo tridimensional homogéneo, que cuando descansa sobre una superficie plana, tiene un solo punto de equilibrio estable y otro inestable. Su existencia fue conjeturada por el matemático ruso Vladímir Arnold en 1995 y probada en 2006 por los científicos húngaros Gábor Domokos y Péter Várkonyi. La forma del gömböc no es única; tiene innumerables variedades, la mayoría de las cuales están muy cerca de una esfera y todas tienen una tolerancia de forma muy estricta (aproximadamente de 0,1 mm por 100 mm).



La solución más famosa tiene una parte superior afilada, como se muestra en la imagen. Su forma ayudó a explicar la estructura corporal de algunas tortugas en relación con su capacidad para volver a la posición de equilibrio después de colocarse al revés.[1][2][3][4] Se han donado copias de gömböc a diversas instituciones y museos, y la más grande se presentó en la Exposición Universal 2010 en Shanghái, China.[5][6] En diciembre de 2017, se instaló una escultura de 4.5 m de altura de un gömböc en el Barrio Corvin en Budapest, Hungría.[7]
Nombre
Si se analiza cuantitativamente en términos de planitud y grosor, es el cuerpo monomonoestático descubierto más parecido a una esfera, aparte de la propia esfera. Debido a esto, fue nombrado gömböc, que significa un diminutivo de gömb ("esfera" en húngaro). Originalmente, el gömböc es un alimento parecido a una salchicha: un estómago relleno de carne de cerdo sazonada, similar a un haggis. Un gomboc (plural en húngaro gombocok) también es una bola de masa dulce hecha con ciruelas y una masa de patata.[8] También existe un relato popular húngaro sobre un gömböc antropomorfo, que se traga a varias personas enteras.[9]
Historia
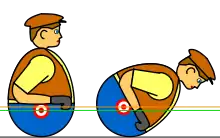
En geometría, un cuerpo con una sola posición de reposo estable se denomina "monoestático", y el término "monomonoestático" se ha acuñado para describir un cuerpo que, además, tiene un solo punto de equilibrio inestable (el poliedro monoestático conocido anteriormente no se considera, ya que tiene tres puntos de equilibrio inestable). Una esfera lastrada para que su centro de masas se desplace del centro geométrico es un cuerpo monomonoestático. Un ejemplo común es un tentetieso (ver figura de la izquierda). No solo tiene un centro de masa bajo, sino que también tiene una forma específica. En estado de equilibrio, el centro de masa y el punto de contacto están en la línea perpendicular al suelo. Cuando se empuja el juguete, su centro de masa se eleva y también se aleja de esa línea. Esto produce un momento de enderezamiento que devuelve el juguete a la posición de equilibrio.
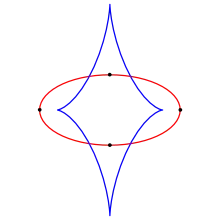
Los ejemplos anteriores de objetos monomonostáticos son necesariamente no homogéneos, es decir, la densidad de su material varía en el cuerpo. La cuestión de si es posible construir un cuerpo tridimensional que sea monomonoestático pero también homogéneo y convexo fue planteado por el matemático ruso Vladímir Arnold en 1995. El requisito de ser convexo es esencial, ya que es trivial construir un cuerpo monomonoestático no convexo (un ejemplo sería una bola con una cavidad en su interior). Convexo significa que una línea recta entre dos puntos cualesquiera del cuerpo se encuentra dentro del cuerpo, o, en otras palabras, que la superficie no tiene regiones hundidas, sino que sobresalen hacia afuera (o al menos son planas) en cada punto. Ya era bien sabido, a partir de una generalización geométrica y topológica del teorema de los cuatro vértices clásico, que una curva plana tiene al menos cuatro valores extremos de su curvatura, específicamente, al menos dos máximos locales y al menos dos mínimos locales (ver figura de la derecha), lo que significa que un objeto monomonoestático (convexo) no existe en dos dimensiones. Mientras que una suposición común era que un cuerpo tridimensional también debería tener al menos cuatro extremos, Arnold conjeturó que este número podría ser más pequeño.[10]
Solución matemática

El problema fue resuelto en 2006 por Gábor Domokos y Péter Várkonyi. Domokos es ingeniero y es el jefe de Mecánica, Materiales y Estructuras en la Universidad de Tecnología y Economía de Budapest. Desde 2004, ha sido el miembro más joven de la Academia Húngara de Ciencias. Várkonyi se formó como arquitecto; fue alumno de Domokos y medallista de plata en la Olimpiada Internacional de Física de 1997. Después de permanecer como investigador postdoctoral en la Universidad de Princeton en 2006–2007, asumió una posición de profesor asistente en la Universidad de Tecnología y Economía de Budapest.[10][11] Domokos había estado trabajando anteriormente en cuerpos monomonoestáticos. En 1995 conoció a Arnold en una importante conferencia de matemáticas en Hamburgo, donde Arnold presentó una exposición plenaria que ilustraba que la mayoría de los problemas geométricos tienen cuatro soluciones o puntos extremos. Sin embargo, en una discusión personal, Arnold cuestionó si cuatro es un requisito para los cuerpos mono-monoestáticos y alentó a Domokos a buscar ejemplos con menos equilibrios.[12]
La prueba rigurosa de la solución se puede encontrar en las referencias de su trabajo.[10] El resumen de los resultados es que el cuerpo convexo homogéneo tridimensional (monomonoestático), que tiene un solo punto de equilibrio estable e inestable, existe y no es único. Tales cuerpos son difíciles de visualizar, describir o identificar. Su forma es diferente a cualquier representante típico de cualquier otra clase geométrica de equilibrio. Deben tener una "planitud" mínima y, para evitar tener dos equilibrios inestables, también deben tener una "delgadez" mínima. Son los únicos objetos no degenerados que tienen al mismo tiempo una planitud y una delgadez mínimas. La forma de esos cuerpos es muy sensible a pequeñas variaciones, fuera de las cuales, ya no son monomonoestáticos. Por ejemplo, la primera solución de Domokos y Várkonyi se parecía mucho a una esfera, con una desviación de forma de solo 10−5. Se descartó, ya que era extremadamente difícil de probar experimentalmente.[13] Su solución publicada era menos sensible; sin embargo, tiene una tolerancia de forma de 10−3, que es de 0.1 mm para un tamaño de 10 cm.[14]
Domokos y su esposa desarrollaron un sistema de clasificación de formas basado en sus puntos de equilibrio mediante el análisis de piedras y anotando sus puntos de equilibrio.[15] En un experimento, analizaron 2000 guijarros recolectados en las playas de la isla griega de Rodas y no encontraron un solo cuerpo monomonoestático entre ellos, lo que ilustra la dificultad de encontrar o construir un cuerpo así.[10][13]
La solución de Domokos y Várkonyi tiene bordes curvos y se asemeja a una esfera con una parte superior aplastada. En la figura superior, descansa en su equilibrio estable. Su posición de equilibrio inestable se obtiene girando la figura 180° alrededor de un eje horizontal. Teóricamente, descansará allí, pero la perturbación más pequeña lo devolverá al punto estable. El gömböc matemático tiene, de hecho, propiedades de tipo esférico. En particular, su planitud y su delgadez son mínimas, y este es el único tipo de objeto no degenerado con esta propiedad.[10] Domokos y Várkonyi están interesados en encontrar una solución poliédrica con una superficie que consista en un número mínimo de planos. Por lo tanto, ofrecen un premio a cualquier persona que encuentre dicha solución, lo que equivale a 10.000 dólares divididos por el número de planos de la solución. Obviamente, se puede aproximar la superficie curvilínea de un gömböc con un número finito de superficies discretas, aunque se estima que se necesitarán miles de planos para lograrlo. Esperan, al ofrecer este premio, estimular una solución radicalmente diferente a la suya.[4]
Relación con los animales

Las propiedades de equilibrio del gömböc están asociadas con la "respuesta de enderezamiento", la capacidad de volverse hacia atrás cuando se coloca al revés, de animales con caparazón como tortugas y escarabajos. Esto puede ocurrir en una pelea o durante el ataque de depredadores, y es crucial para su supervivencia. La presencia de un solo punto estable e inestable en un gömböc significa que volverá a una posición de equilibrio sin importar cómo se empuje o gire. Mientras que los animales relativamente planos (como los escarabajos) dependen en gran medida del impulso y empuje que se desarrolla al mover sus extremidades y alas, las extremidades de muchas tortugas en forma de cúpula son demasiado cortas para ser útiles para enderezarse.
Domokos y Várkonyi pasaron un año midiendo tortugas en el zoológico de Budapest, el Museo Húngaro de Historia Natural y varias tiendas de mascotas en Budapest, digitalizando y analizando sus conchas, e intentando "explicar" las formas y funciones de su cuerpo desde su trabajo de geometría. Su primer artículo de biología fue rechazado cinco veces, pero finalmente fue aceptado por la revista de biología "Proceedings of the Royal Society". Luego se popularizó de inmediato en varios informes de noticias científicas, incluidos los de las revistas científicas más prestigiosas como "Nature" [3] y "Science".[4][16]
El modelo presentado puede resumirse en que las conchas planas en tortugas son una ventaja para nadar y cavar. Sin embargo, los bordes afilados de la cáscara dificultan el rodamiento. Esas tortugas generalmente tienen patas y cuello largos y los usan activamente para empujarse contra el suelo, para volver a la posición normal si se colocan boca abajo. Por el contrario, las tortugas "redondas" fácilmente se enderezan solas; las que tienen extremidades más cortas y las utilizan poco para recuperar el equilibrio perdido, aunque siempre se necesitaría algo de movimiento de la extremidad debido a la forma imperfecta del caparazón, las condiciones del suelo, etc. Las conchas redondas también resisten mejor el aplastamiento por mordedura de un depredador y son mejores para la regulación térmica.[1][2][3][4]

La explicación de la forma del cuerpo de la tortuga, utilizando la teoría del Gömböc, ya ha sido aceptada por algunos biólogos. Por ejemplo, Robert McNeill Alexander, uno de los pioneros de la biomecánica moderna, lo utilizó en su conferencia plenaria sobre optimización en evolución en 2008.[17]
No se conocen otras aplicaciones prácticas de los gömböcs, probablemente porque es una solución exótica para un caso idealizado de sólido homogéneo. Aunque la recuperación del equilibrio es crucial en áreas como la robótica, normalmente se logra simplemente haciendo que las partes inferiores sean más pesadas.[3]
Producción
La estricta tolerancia de forma de los gömböcs dificultó su producción. El primer prototipo de un gömböc se fabricó en el verano de 2006 con tecnología tridimensional de prototipado rápido. Sin embargo, su precisión estaba por debajo de los requisitos, y el gömböc a menudo se quedaba atascado en una posición intermedia en lugar de volver al equilibrio estable. La tecnología se mejoró para aumentar la precisión espacial al nivel requerido y para utilizar varios materiales de construcción. En particular, los sólidos transparentes (especialmente de colores claros) son visualmente atractivos, ya que demuestran la composición homogénea. Los materiales actuales para los gömböcs incluyen diversos metales y aleaciones, plásticos como elplexiglás, piedras como el mármol, cerámica,[18] y plástico moldeado por inyección. Las propiedades de equilibrio de un gömböc se ven afectadas por defectos mecánicos y polvo tanto en su cuerpo como en la superficie sobre la que descansa. Si está dañado, el proceso de restauración de la forma original es más complejo que producir uno nuevo.[19] Aunque en teoría las propiedades de equilibrio no deberían depender del material y el tamaño del objeto, en la práctica, tanto los gömböcs más grandes como los más pesados tienen mejores posibilidades de volver al punto de equilibrio en caso de defectos.[20]
Domokos y Várkonyi presentaron el primer gömböc como regalo a Vladimir Arnold con motivo de su 70 cumpleaños.[18] Uno de los gömböcs más grande tiene aproximadamente 3 metros de altura y 3 metros de ancho. Se exhibió en la exposición principal del pabellón húngaro en la Exposición Universal 2010 de Shanghái, en China.[5][6]
Medios de comunicación
La invención del gömböc ha estado en el foco de atención del público y los medios de comunicación, repitiendo el éxito de otro húngaro, el inventor Ernő Rubik, cuando diseñó el cubo de Rubik en 1974.[21] Por su descubrimiento, Domokos y Várkonyi fueron condecorados con la Orden del Mérito de la República de Hungría.[22] The New York Times Magazine seleccionó el gömböc como una de las 70 ideas más interesantes del año 2007.[23][24]
El sitio web Stamp News[25] muestra los nuevos sellos emitidos el 30 de abril de 2010 por Hungría, que ilustran un gömböc en diferentes posiciones. Los folletos de sellos están dispuestos de tal manera que el gömböc parece cobrar vida cuando se voltea el folleto. Los sellos se emitieron en asociación con el gömböc en exhibición en la Expo Mundial 2010 (del 1 de mayo al 31 de octubre). El evento también fue cubierto por la revista Linn's Stamp News.[26]
En la serie de Internet Video Game High School, un antropomorfizado Gömböc es el antagonista de un juego infantil creado por el personaje Ki Swan en el episodio de la temporada 1 "Cualquier juego en la casa".
El juego de rol webcomic Darths and Droids[27] presentó un Gömböc como un dado unilateral en septiembre de 2018.
Véase también
Referencias
- Domokos, G.; Varkonyi, P.L. (2008). «Geometry and self-righting of turtles» (free download pdf). Proc. R. Soc. B 275 (1630): 11-17. PMC 2562404. PMID 17939984. doi:10.1098/rspb.2007.1188.
- Summers, Adam (March 2009). «The Living Gömböc. Some tortoise shells evolved the ideal shape for staying upright». Natural History 118 (2): 22-23.
- Ball, Philip (16 de octubre de 2007). «How tortoises turn right-side up». Nature News. doi:10.1038/news.2007.170.
- Rehmeyer, Julie (5 de abril de 2007). «Can't Knock It Down». Science News.
- Hungary Pavilion features Gomboc, expo.shanghaidaily.com (12 July 2010)
- New geometric shape "Gomboc" featured at Shanghai Expo, English.news.cn, 19 August 2010
- «Világritkaság szobor Budapesten - fotók» (en húngaro). Archivado desde el original el 3 de enero de 2018. Consultado el 2 de enero de 2018.
- A kis gömböc Archivado el 20 de julio de 2009 en Wayback Machine., a folk tale in Hungarian. sk-szeged.hu
- Varkonyi, P.L., Domokos, G. (2006). «Mono-monostatic bodies: the answer to Arnold's question». The Mathematical Intelligencer 28 (4): 34-38. doi:10.1007/bf02984701.
- Inventors. gomboc-shop.com.
- Domokos, Gábor (2008). «My Lunch with Arnol'd». The Mathematical Intelligencer 28 (4): 31. doi:10.1007/BF02984700. Archivado desde el original el 26 de julio de 2011. Consultado el 28 de octubre de 2018.
- Freiberger, Marianne (May 2009). «The story of the gömböc». Plus magazine.
- «The first gömböc». gomboc.eu. Archivado desde el original el 12 de noviembre de 2017. Consultado el 28 de octubre de 2018.
- Varkonyi, P.L.; Domokos, G. (2006). «Static Equilibria of Rigid Bodies: Dice, Pebbles, and the Poincare-Hopf Theorem». Journal of Nonlinear Science 16 (3): 255. doi:10.1007/s00332-005-0691-8.
- «Gömböc – Finding Consilience». quickswood.com. 14 de febrero de 2008. Archivado desde el original el 20 de febrero de 2015. Consultado el 28 de octubre de 2018.
- Professor Alexander on the Turtles and the Gömböc Archivado el 15 de septiembre de 2009 en Wayback Machine.. Tetrapod Zoology (24 May 2008).
- Knight's Cross for the Gömböc, Gömböc for Arnold Archivado el 15 de septiembre de 2009 en Wayback Machine.. Moscow, 20 August 2007. Gomboc.eu.
- Usage of a gömböc. gomboc-shop.com.
- Does the behavior of a gömböc depend on the size or the material?. gomboc-shop.com.
- «Boffins develop a 'new shape' called Gomboc». Melbourne: Theage.com.au. 13 de febrero de 2007.
- A Gömböc for the Whipple. News, University of Cambridge (27 April 2009)
- Thompson, Clive (9 December 2007) Self-Righting Object, The Archivado el 15 de septiembre de 2009 en Wayback Machine.. New York Times Magazine.
- Per-Lee, Myra (9 December 2007) Whose Bright Idea Was That? The New York Times Magazine Ideas of 2007 Archivado el 11 de marzo de 2021 en Wayback Machine.. Inventorspot.com.
- Better City – Better Life: Shanghai World Expo 2010 Archivado el 16 de agosto de 2017 en Wayback Machine.. Stampnews.com (22 November 2010). Retrieved on 20 October 2016.
- McCarty, Denise (28 June 2010) "World of New Issues: Expo stamps picture Hungary's Gömböc, Iceland's ice cube". Linn's Stamp News p. 14
- Darths and Droids