Gas real
Un gas real, en oposición a un gas ideal, es un gas que exhibe propiedades que no pueden ser explicadas enteramente utilizando la ley de los gases ideales. Para entender el comportamiento de los gases reales deben considerarse los siguientes efectos:
- efectos de compresibilidad
- capacidad calorífica específica variable
- fuerzas de Van der Waals
- efectos termodinámicos del no-equilibrio
- cuestiones de disociación molecular y reacciones elementales con composición variable.
Para la mayoría de aplicaciones, un análisis tan detallado es innecesario, y la aproximación de gas ideal puede ser utilizada con razonable precisión. En cambio, cerca del punto de condensación de los gases, cerca de puntos críticos, a muy altas presiones y en otros casos menos usuales, es necesario emplear modelos de gas real.
Modelos
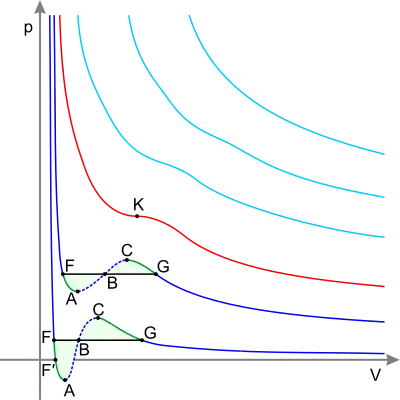
Curvas azul oscuro – isotermas debajo de la temperatura crítica. Secciones verdes – estados metaestables.
Sección a la izquierda del punto F – líquido normal.
Punto F – punto de ebullición.
Línea FG – equilibrio de fases líquida y gaseosa.
Section FA – líquido supercalentado.
Section F′A – líquido "estirado" (stretched) (p<0).
Section AC – extensión analítica de la isoterma, físicamente imposible.
Section CG – vapor superenfriado.
Point G – punto de rocío.
Gráfica a la derecha del punto G – gas normal.
Las áreas FAB y GCB son iguales.
Curva roja – Isoterma crítica.
Punto K – punto crítico.
Curvas azul claro – isotermas supercríticas.
Modelo de Van der Wals
Los gases reales son ocasionalmente modelados tomando en cuenta su masa y volumen molares
donde P es la presión, T es la temperatura, R es la constante de los gases ideales, y Vm es el volumen molar. "a" y "b" son parámetros que son determinados empíricamente para cada gas, pero en ocasiones son estimados a partir de su temperatura crítica (Tc) y su presión crítica (Pc) utilizando estas relaciones:
Modelo de Redlich–Kwong
La ecuación de Redlich–Kwong es otra ecuación de dos parámetros que es utilizada para modelar gases reales. Es casi siempre más precisa que la ecuación de Van der Waals, y en ocasiones más precisa que algunas ecuaciones de más de dos parámetros. La ecuación es
donde "a" y "b" son dos parámetros empíricos que no son los mismos parámetros que en la ecuación de Van der Waals. Estos parámetros pueden ser determinados:
Modelo de Berthelot y de Berthelot modificado
La ecuación de Berthelot (nombrada en honor de D. Berthelot[1]) es muy raramente usada,
pero la versión modificada es algo más precisa
Modelo de Dieterici
Este modelo (nombrado en honor de C. Dieterici[2]) cayó en desuso en años recientes
.
Modelo de Clausius
La ecuación de Clausius (nombrada en honor de Rudolf Clausius) es una ecuación muy simple de tres parámetros usada para modelar gases.
donde
y donde Vc es el volumen crítico.
Modelo virial
La ecuación virial deriva a partir de un tratamiento perturbacional de la mecánica estadística.
o alternativamente
donde B, C, D, B′, C′ y D′ ,son constantes dependientes de la temperatura.
Modelo de Peng–Robinson
Esta ecuación de dos parámetros (nombrada en honor de D.-Y. Peng y D. B. Robinson)[3] tiene la interesante propiedad de ser útil para modelar algunos líquidos además de gases reales.
Modelo de Wohl
La ecuación de Wohl (nombrada en honor de A. Wohl[4]) está formulada en términos de valores críticos, haciéndola útil cuando no están disponibles las constantes de gases reales.
donde
.
Modelo de Beattie–Bridgman
Esta ecuación está basada en cinco constantes determinadas experimentalmente.[5] Está expresada como
donde
Se sabe que esta ecuación es razonablemente precisa para densidades hasta alrededor de 0.8 ρcr, donde ρcr es la densidad de la sustancia en su punto crítico. Las constantes que aparecen en la ecuación superior están dadas en la siguiente tabla cuando P está en kPa, v está en , T está en K y R=8.314[6]
| Gas | A0 | a | B0 | b | c |
|---|---|---|---|---|---|
| Aire | 131.8441 | 0.01931 | 0.04611 | -0.001101 | 4.34×104 |
| Argon, Ar | 130.7802 | 0.02328 | 0.03931 | 0.0 | 5.99×104 |
| Dióxido de carbono, CO2 | 507.2836 | 0.07132 | 0.10476 | 0.07235 | 6.60×105 |
| Helio, He | 2.1886 | 0.05984 | 0.01400 | 0.0 | 40 |
| Hidrógeno, H2 | 20.0117 | -0.00506 | 0.02096 | -0.04359 | 504 |
| Nitrógeno, N2 | 136.2315 | 0.02617 | 0.05046 | -0.00691 | 4.20×104 |
| Oxígeno, O2 | 151.0857 | 0.02562 | 0.04624 | 0.004208 | 4.80×104 |
Modelo de Benedict–Webb–Rubin
La ecuación de Benedict–Webb–Rubin es otra ecuación de estado, referida a veces como ecuación BWR y otra como ecuación BWRS:
donde d es la densidad molar y "a", "b", "c", "A", "B", "C", "α", y "γ" son constantes empíricas.
Véase también
Referencias
- D. Berthelot en Travaux et Mémoires du Bureau international des Poids et Mesures – Tome XIII (París: Gauthier-Villars, 1907)
- C. Dieterici, Ann. Phys. Chem. Wiedemanns Ann. 69, 685 (1899)
- Peng, D. Y., y Robinson, D. B. (1976). «A New Two-Constant Equation of State». Industrial and Engineering Chemistry: Fundamentals 15: 59-64. doi:10.1021/i160057a011.
- A. Wohl "Investigation of the condition equation", Zeitschrift für Physikalische Chemie (Leipzig) 87 pp. 1–39 (1914)
- Yunus A. Cengel y Michael A. Boles, Thermodynamics: An Engineering Approach, 7a. edición, McGraw-Hill, 2010, ISBN 007-352932-X
- Gordan J.Van Wylen y Richard E.Sonntage, Fundamental of classical Thermodynamics, 3a. ed, Nueva York, John Wiley &Sons, 1986 p. 46 tabla 3.3
- Dilip Kondepudi, Ilya Prigogine, Modern Thermodynamics, John Wiley & Sons, 1998, ISBN 0-471-97393-9
- Hsieh, Jui Sheng, Engineering Thermodynamics, Prentice-Hall Inc., Englewood Cliffs, Nueva Jersey 07632, 1993. ISBN 0-13-275702-8
- Stanley M. Walas, Phase Equilibria in Chemical Engineering, Butterworth Publishers, 1985. ISBN 0-409-95162-5
- M. Aznar y A. Silva Telles, A Data Bank of Parameters for the Attractive Coefficient of the Peng-Robinson Equation of State, Braz. J. Chem. Eng. vol. 14 no. 1 São Paulo Mar. 1997, ISSN 0104-6632
- An introduction to thermodynamics por Y. V. C. Rao
- The corresponding-states principle and its practice: thermodynamic, transport and surface properties of fluids por Hong Wei Xiang
Enlaces externos
- (en inglés) Equations of State
- Esta obra contiene una traducción derivada de «Real gas» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.