Grafo F26A
En el campo matemático de la teoría de grafos, el grafo F26A es un grafo cúbico bipartito simétrico con 26 vértices y 39 aristas.[1]
| Grafo F26A | ||
|---|---|---|
 El grafo F26A es hamiltoniano | ||
| Vértices | 26 | |
| Aristas | 39 | |
| Radio | 5 | |
| Diámetro | 5 | |
| Cintura | 6 | |
| Automorfismos | 78 (C13⋊C6) | |
| Número cromático | 2 | |
| Índice cromático | 3 | |
| Propiedades |
Grafo de Cayley Simétrico Cúbico Hamiltoniano[1] | |
Tiene coloración de grafos 2, índice cromático 3, diámetro 5, radio 5 y cintura 6.[2] También es un grafo 3-vértices-conectado y 3-aristas-conectado.
El grafo F26A es hamiltoniano y se puede describir mediante la notación LCF como [−7, 7]13.
Propiedades algebraicas
El grupo de automorfismos del grafo F26A es un grupo de orden 78.[3] Actúa transitivamente sobre los vértices, sobre las aristas y sobre los arcos del grafo. Por lo tanto, el grafo F26A es un grafo simétrico (aunque no distancia transitivo). Tiene automorfismos que llevan cualquier vértice a cualquier otro vértice y cualquier arista a cualquier otra arista. Según el Censo de Forster, el grafo F26A es el único grafo simétrico cúbico en 26 vértices.[2] También es un grafo de Cayley para el grupo diédrico D26, generado por a, ab y ab4, donde:[4]
El grafo F26A es el grafo cúbico más pequeño donde el automorfismo agrupa acciones regularmente en arcos (es decir, en aristas que se considera que tienen una dirección).[5]
El polinomio característico del grafo F26A es igual a:
Otras propiedades
El grafo F26A se puede incrustar como un mapa regular quiral en el toro, con 13 caras hexagonales. El grafo dual para este embebido es isomorfo al grafo de Paley de orden 13.
Galería
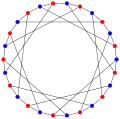 La coloración del grafo F26A graph es 2
La coloración del grafo F26A graph es 2 El índice cromático del grafo F26A es 3
El índice cromático del grafo F26A es 3 Dibujo alternativo del grafo F26A
Dibujo alternativo del grafo F26A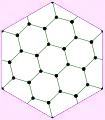 El grafo F26A embebido en un toro
El grafo F26A embebido en un toro
Referencias
- Weisstein, Eric W. «Cubic Symmetric Graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41–63, 2002.
- Royle, G. F026A data
- «Yan-Quan Feng and Jin Ho Kwak, Cubic s-Regular Graphs, p. 67.». Archivado desde el original el 26 de agosto de 2006. Consultado el 12 de marzo de 2010.
- Yan-Quan Feng and Jin Ho Kwak, "One-regular cubic graphs of order a small number times a prime or a prime square," J. Aust. Math. Soc. 76 (2004), 345-356 .