Grafo simétrico

En el campo matemático de la teoría de grafos, un grafo G es simétrico si, dado cualquier par de pares de vértices adyacentes u1—v1 y u2—v2 de G, existe un automorfismo

f: V(G) → V(G)
El grafo de Petersen es un grafo simétrico (cúbico) . Cualquier par de vértices adyacentes se puede mapear a otro par por un automorfismo, ya que cualquier anillo de cinco vértices se puede mapear a cualquier otro.

tal que

f(u1) = u2 and f(v1) = v2.[1]

En otras palabras, un grafo es simétrico si su grupo automórfico actúa transitivamente sobre pares ordenados de vértices adyacentes (es decir, sobre los bordes considerados como teniendo una dirección).[2] Este grafo se denomina a veces también 1-arco-transitivo.[2][3]

Por definición (ignorando u1 y u2), un grafo simétrico sin vértices aislados también debe ser vértice transitivo.[1] Ya que la definición anterior mapea un borde al otro, una grafo simétrico también debe ser arista transitivo. Sin embargo, un grafo arista transitivo no es necesariamente simétrico, ya que a—b puede mapear a c—d, pero no a d—c. Los grafos semi-simétricos, por ejemplo, son arista transitivos y regulares, pero no vértice transitivos.


Cada grafo simétrico conectado debe por lo tanto ser a la vez vértice transitivo y arista transitivo, y lo contrario es cierto para los grafos de grado impar.[3] Sin embargo, para los grafos de grado par, existen grafos conectados que son vértice transitivos y arista transitivos, pero no simétricos.[4] Tales grafos son llamados semi-transitivos.[5] el grafo semi-transitivo conectado más pequeño es el grafo de Holt, de grado 4 y con 27 vértices.[1][6] Confusamente, algunos autores usan el término "grafo simétrico" hablando de grafos que son vértice transitivos y arista transitivos, pero no son arco transitivos. Una definición así incluiría los grafos semi-transitivos, que están excluidos en virtud de la definición anterior.

Un grafo distancia-transitivo es aquel donde en lugar de considerar pares de vértices adyacentes (es decir, los vértices separados por una arista), la definición comprende dos pares de vértices, cada uno a la misma distancia. Tales grafos son automáticamente simétricos, por definición.[1]

Un t-arco es definido como una secuencia de t+1 vértices, tal que dos vértices consecutivos cualesquiera en la secuencia son adyacentes, y cualquier vértice repetido está separado por lo menos 2 pasos. Un grafo t-transitivo es un grafo tal que el grupo automórfico actúa transitivamente sobre t-arcos, pero no sobre (t+1)-arcos. Ya que 1-arcos son simplemente aristas, cada grafo simétrico de grado 3 o mayor debe ser t-transitivo para alguna t, y el valor de t puede ser usado para clasificar los grafos simétricos. Por ejemplo, el cubo es 2-transitivo.[1]

Ejemplos

La combinación de la condición de simetría con la restricción de que los grafos sean cúbicos (es decir, todos los vértices tengan grado 3) es muy restrictiva, y tales grafos son lo suficientemente raros para ser enumerados. El censo de Foster incluyó esa lista.[7] El censo Foster fue iniciado en 1930 por Ronald M. Foster mientras era empleado de los Laboratorios Bell,[8] y en 1988 (cuando Foster tenía 92 años[1]) el censo Foster actualizado (listando todos los grafos simétricos cúbicos de hasta 512 vértices) fue publicado en forma de libro.[9] Los primeros trece elementos de la lista son grafos simétricos cúbicos de hasta 30 vértices[10][11] (diez de ellos son también distancia-transitivos; las excepciones son como se indica):

VérticesDiámetroCinturaGrafoNotas
413El grafo completo K4distancia-transitivo, 2-transitivo
624El grafo bipartito completo K3,3distancia-transitivo, 3-transitivo
834Los vértices y las aristas del cubodistancia-transitivo, 2-transitivo
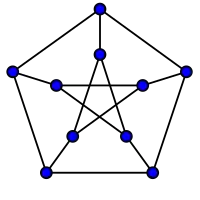
1025El grafo de Petersendistancia-transitivo, 3-transitivo
1436El grafo de Heawooddistancia-transitivo, 4-transitivo
1646El grafo de Möbius-Kantor2-transitivo
1846El grafo de Papodistancia-transitivo, 3-transitivo
2055Los vértices y las aristas del dodecaedrodistancia-transitivo, 2-transitivo
2056El grafo de Desarguesdistancia-transitivo, 3-transitivo
2446El grafo de Nauru (el grafo de Petersen generalizado G(12,5))2-transitivo
2656El grafo F26A[11]1-transitivo
2847El grafo de Coxeterdistancia-transitivo, 3-transitivo
3048El grafo de Tutte-Coxeterdistancia-transitivo, 5-transitivo

Otros grafos simétricos cúbicos conocidos son el grafo de Dyck, el grafo de Foster y el grafo de Biggs–Smith. Los diez grafos distancia-transitivos listado arriba, junto con el grafo de Foster y el grafo de Biggs–Smith, son los únicos grafos cúbicos distancia-transitivs.

Los grafos simétricos no cúbicos incluyen ciclos (de grado 2), grafos completos (de grado 4 o mayor cuando tienen 5 o más vértices), grafos hipercubos (de grado 4 o mayor cuando tienen 16 o más vértices), y los grafos formados por los vértices y aristas del octaedro, icosaedro, cuboctaedro, and icosidodecaedro. El grafo de Rado es un ejemplo de grafo simétrico con vértices infinitos y grado infinito.


Véase también

Referencias
  1. Biggs, Norman (1993). Algebraic Graph Theory (2nd edición). Cambridge: Cambridge University Press. pp. 118-140. ISBN 0-521-45897-8.
  2. Godsil, Chris; Royle, Gordon (2001). Algebraic Graph Theory. Nueva York: Springer. p. 59. ISBN 0-387-95220-9.
  3. Babai, L (1996). «Automorphism groups, isomorphism, reconstruction». En Graham, R; Groetschel, M; Lovasz, L, eds. Handbook of Combinatorics. Elsevier. Archivado desde el original el 11 de junio de 2010. Consultado el 16 de agosto de 2014.
  4. Bouwer, Z. "Vertex and Edge Transitive, But Not 1-Transitive Graphs." Canad. Math. Bull. 13, 231–237, 1970.
  5. Gross, J.L. and Yellen, J. (2004). Handbook of Graph Theory. CRC Press. p. 491. ISBN 1-58488-090-2.
  6. Holt, Derek F. (1981). «A grafo which is edge transitivo but not arc transitive». Journal of Graph Theory 5 (2): 201-204. doi:10.1002/jgt.3190050210..
  7. Marston Conder, Trivalent symmetric grafos on up to 768 vertices, J. Combin. Math. Combin. Comput, vol. 20, pp. 41–63
  8. Foster, R. M. "Geometrical Circuits of Electrical Networks." Transactions of the American Institute of Electrical Engineers 51, 309–317, 1932.
  9. "The Foster Census: R.M. Foster's Census of Connected Symmetric Trivalent Graphs", by Ronald M. Foster, I.Z. Bouwer, W.W. Chernoff, B. Monson and Z. Star (1988) ISBN 0-919611-19-2
  10. Biggs, p. 148
  11. Weisstein, Eric W., "Cubic Symmetric Graph", from Wolfram MathWorld.

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.