Hiperestaticidad
En estática, una estructura es hiperestática o estáticamente indeterminada cuando está en equilibrio pero las ecuaciones de la estática resultan insuficientes para determinar todas las fuerzas internas o las reacciones. Existen diversas formas de hiperestaticidad:
- Una estructura es internamente hiperestática si las ecuaciones de la estática no son suficientes para determinar los esfuerzos internos de la misma.
- Una estructura es externamente hiperestática si las ecuaciones de la estática no son suficientes para determinar fuerzas de reacción de la estructura al suelo o a otra estructura.
Una estructura es completamente hiperestática si es internamente y externamente hiperestática.
Ejemplo
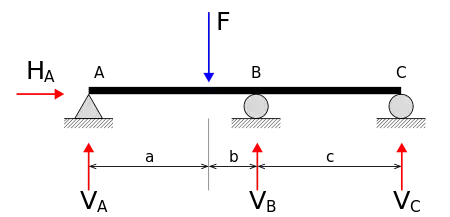
En la viga hiperestática representada en la figura existen cuatro reacciones para determinar las fuerzas que la viga transmite a sus tres apoyos, tres componentes verticales VA, VB, VC y una componente horizontal HA (F representa aquí la fuerza exterior). A base de las leyes de Newton, las ecuaciones de equilibrio de la estática aplicables a esta estructura plana en equilibrio son que la suma de componentes verticales debe ser cero, que la suma de fuerzas horizontales debe ser cero y que la suma de momentos respecto a cualquier punto del plano debe ser cero:
Desarrollando las ecuaciones anteriores:
Puesto que se tienen solo tres ecuaciones linealmente independientes y cuatro fuerzas o componentes desconocidos (VA, VB, VC y HA) con solo estas ecuaciones resulta imposible calcular las reacciones y por tanto la estructura es hiperestática (de hecho, externamente hiperestática).
Solo cuando se considera las propiedades elásticas del material y se aplican las debidas ecuaciones de compatibilidad de las deformaciones el problema puede ser resuelto (siendo estáticamente indeterminado es al mismo tiempo elásticamente determinado). Las reacciones en el ejemplo anterior pueden determinarse por ejemplo mediante el teorema de los tres momentos que lleva a que:
Calculando las reacciones verticales a partir del diagrama de esfuerzos cortantes se llega a las expresiones:
Métodos de cálculo para estructuras hiperestáticas (interior y exterior)
Referencias
Bibliografía
- Luis Ortiz Berrocal (2007). Resistencia de materiales, Madrid: Ed. McGraw-Hill. ISBN 9788448156336