Hipotenusa
La hipotenusa es el lado opuesto al ángulo recto en un triángulo rectángulo, y resulta ser su lado de mayor longitud.
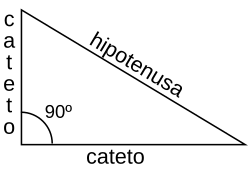
Según el teorema de Pitágoras, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los otros dos lados del triángulo rectángulo, denominados catetos.
Etimología
La palabra hipotenusa proviene del término griego ὑποτείνουσα, un compuesto de hipó, ‘debajo’, y téino, ‘estirar’.[1]
Relaciones métricas
- Establece que el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos. Es decir, si a representa la longitud de la hipotenusa, b y c la de los catetos, es:
Por lo cual:
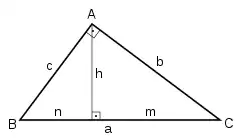
- La longitud de la hipotenusa es igual a la suma de las longitudes de las proyecciones ortogonales de ambos catetos.
- El cuadrado de la longitud de un cateto es igual al producto de la longitud de su proyección ortogonal sobre la hipotenusa por la longitud de ésta.
- El cuadrado de la longitud de la altura es igual al producto de las longitudes de las proyecciones ortogonales de los catetos sobre la hipotenusa.
Proposiciones
- En un triángulo inscrito la hipotenusa coincide con un diámetro tanto como segmento cuanto en longitud.
- El radio de una circunferencia circunscrita es igual a la mitad de la longitud del diámetro.
- En un triángulo rectángulo inscrito un radio coincide con la mediana que une la hipotenusa con el ángulo recto.
- De los triángulos rectángulos que tienen la misma hipotenusa y constante la suma de sus catetos, el que tiene mayor área es el triángulo rectángulo isósceles.
- Una de las diagonales de un rectángulo determina dos triángulos rectángulos iguales ( congruentes), siendo la diagonal, la hipotenusa común.
Razones trigonométricas
Mediante razones trigonométricas se puede obtener el valor de los dos ángulos agudos, y , del triángulo rectángulo.
Conocida la longitud de la hipotenusa y la de un cateto , la razón entre ambos es:
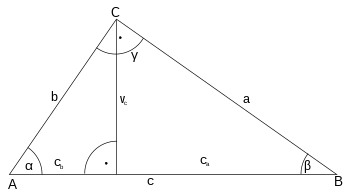
Por tanto, la función trigonométrica inversa es:
Siendo el valor del ángulo opuesto al cateto .
El ángulo contiguo al cateto será = 90° –
También se puede obtener el valor del ángulo mediante la ecuación:
Siendo el otro cateto.
Véase también
Referencias
- Schwartzman, Steven The Words of Mathematics, An Etymological Dictionary of Mathematical Terms used in English, Publicado por la Asociación de matemáticos de Estados Unidos. (En inglés)
Enlaces externos
 Wikcionario tiene definiciones y otra información sobre hipotenusa.
Wikcionario tiene definiciones y otra información sobre hipotenusa. Wikimedia Commons alberga una categoría multimedia sobre Hipotenusa.
Wikimedia Commons alberga una categoría multimedia sobre Hipotenusa.