Indicatriz de Dupin
En la geometría diferencial de superficies curvas en el espacio, una indicatriz es una sección cónica plana, que describe el comportamiento de la curvatura local de una superficie en un punto determinado.[1] El término fue introducido por el matemático francés Charles Dupin a principios del siglo XIX y, por lo tanto, también se le llama indicatriz de Dupin.[2]
Descripción geométrica
En un entorno suficientemente pequeño de un punto de una superficie (dada, por ejemplo, por z = f(x,y) con f dos veces continuamente diferenciable), la superficie puede aproximarse con la precisión que se desee mediante una cuádrica, es decir, generando una superficie de segundo orden de la forma z = g(x,y). Para generar la indicatriz de Dupin, esta cuádrica osculadora es cortada por un plano paralelo y tan próximo como se desee al plano tangente, desplazado en la dirección normal a la superficie o en la dirección opuesta a ella. Pueden producirse cuatro casos:
- Las intersecciones están siempre vacías; la cuádrica osculadora ha degenerado en un plano tangencial. Todavía se genera un punto parabólico (porque el determinante de la segunda forma fundamental se anula).
- Las intersecciones constan de dos líneas rectas paralelas a un lado de la superficie y del conjunto vacío al otro (por ejemplo, en el caso de un cilindro). Entonces, se habla de un punto parabólico de la superficie. La cuádrica osculadora es un cilindro parabólico (consúltese el enlace web que figura al final del artículo).
- La intersección es una elipse cuando se desplaza el plano en la dirección normal y queda vacía cuando se desplaza en la dirección opuesta (por ejemplo, en el caso de una superficie esférica). Entonces, el punto se denomina punto elíptico de la superficie. La cuádrica osculadora es un paraboloide.
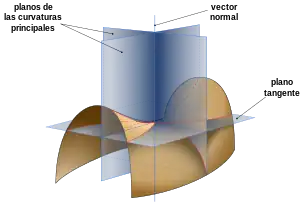
- Dependiendo de la dirección del desplazamiento, la intersección resulta en una u otra hipérbola de un par de hipérbolas conjugadas (por ejemplo, en el caso de una superficie con forma de silla de montar; véase la imagen que encabeza el artículo). Entonces se habla de un punto hiperbólico de la superficie. La cuádrica osculadora es un paraboloide.
Caracterización según las curvaturas principales
Estos cuatro casos se suelen diferenciar utilizando las dos curvaturas principales de la superficie, teniendo en cuenta lo siguiente:
- Ambas curvaturas principales son cero si la cuádrica osculadora degenera en un plano tangente.
- Exactamente una de las dos curvaturas principales es cero en el caso de un punto parabólico con una cuádrica osculadora no plana.
- Ambas tienen el mismo signo en el caso de un punto elíptico.
- Ambas tienen signos diferentes en el caso de un punto hiperbólico.
El producto de las dos curvaturas principales, denominado curvatura de Gauss, es positivo en el caso de un punto elíptico y negativo en el caso de un punto hiperbólico, y en caso contrario es cero.
Descripción formal
La indicatriz de Dupin se encuentra en el plano tangente a la superficie en el punto , y es el conjunto de los extremos de los segmentos dispuestos desde el punto en la dirección en el plano tangente y que tienen una longitud igual a , donde es el valor absoluto de la curvatura normal de la superficie en el punto en la dirección . La ecuación de la indicatriz de Dupin tiene la forma:
donde es el vector del plano tangente, y es la segunda forma fundamental de la superficie en el punto .
Aplicaciones
- El elipsoide de índices de refracción es una indicatriz utilizada en óptica para calcular la birrefringencia.
- La indicatriz de Tissot se utiliza para comprobar las propiedades de distorsión de los sistemas de proyección cartográfica.
Referencias
- Faydor L. Litvin, Alfonso Fuentes (2004). Gear Geometry and Applied Theory. Cambridge University Press. p. 193. ISBN 9781139455558. Consultado el 18 de septiembre de 2023.
- O'Connor, John J.; Robertson, Edmund F., «Indicatriz de Dupin» (en inglés), MacTutor History of Mathematics archive, Universidad de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Indicatriz+de+Dupin.html.
Bibliografía
- Volkmar Wünsch: Geometría diferencial. Curvas y superficies. Teubner, Stuttgart et al. 1997, ISBN 3-8154-2095-4, pliDSqmVAc6g_gaIy9GuCw&sa=X&oi=libro_resultado&ct= resultado&resnum=9 Google Libros
Enlaces externos
- Imágenes de cuádricas solo las superficies denominadas allí cuádricas parabólicas aparecen como cuádricas osculadoras. Consultado el 13 de agosto de 2009.