Curvaturas principales
En geometría diferencial, las dos curvaturas principales en un punto dado de una superficie son los valores máximo y mínimo de su curvatura, expresados por los autovalores del operador de forma en ese punto. Miden cómo la superficie se dobla en distinto grado en diferentes direcciones con respecto a un punto dado de una superficie.
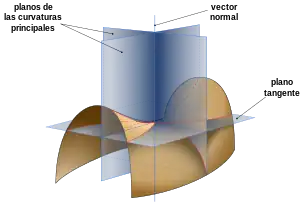
Discusión
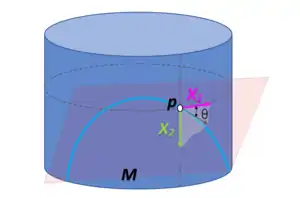
En cada punto p de una superficie diferenciable en un espacio euclídeo tridimensional se puede elegir un vector normal unitario. Un plano normal en p es aquel que contiene el vector normal y, por lo tanto, también contendrá una dirección única tangente a la superficie y cortará a la superficie generando una curva plana, llamada sección normal. En general, esta curva tendrá diferentes curvaturas para diferentes planos normales en p. Las curvaturas principales en p, denominadas k1 y k2, son los valores máximo y mínimo de esta curvatura.
Aquí la curvatura de una curva es por definición el recíproco del radio de la circunferencia osculatriz. La curvatura se considera positiva si la curva gira en la misma dirección que la normal elegida para la superficie y, en caso contrario, se considera negativa. Las direcciones en el plano normal donde la curvatura toma sus valores máximo y mínimo son siempre perpendiculares, si k1 no es igual a k2, resultado obtenido por Euler (1760), y se llaman direcciones principales. Desde una perspectiva moderna, este teorema se deriva del teorema de descomposición espectral porque estas direcciones son como los ejes principales de un tensor simétrico: su segunda forma fundamental. Jean Gaston Darboux realizó un análisis sistemático de las curvaturas principales y las direcciones principales, utilizando el marco de Darboux.
El producto k1k2 de las dos curvaturas principales es la curvatura de Gauss, K; y el promedio (k1 + k2)/2 es la curvatura media, H.
Si al menos una de las curvaturas principales es cero en cada punto, entonces la curvatura de Gauss será 0 y la superficie será desarrollable. Para una superficie minimal, la curvatura media es cero en cada punto.
Definición formal
Sea M una superficie en el espacio euclídeo con la segunda forma fundamental . A continuación, se fija un punto p ∈ M, y un base ortonormal X1, X2 de vectores tangentes en p. Entonces, las curvaturas principales son los valores propios de la matriz simétrica:
Si se seleccionan X1 y X2 de modo que la matriz sea una matriz diagonal, entonces se denominan direcciones principales. Si la superficie está orientada, entonces a menudo se requiere que el par (X1, X2) esté orientado positivamente con respecto a la orientación dada.
Sin hacer referencia a una base ortonormal particular, las curvaturas principales son los autovalores del operador de forma y las direcciones principales son sus autovectores.
Generalizaciones
Para hipersuperficies en espacios euclídeos de dimensiones superiores, las curvaturas principales pueden definirse de forma directamente análoga. Las curvaturas principales son los valores propios de la matriz de la segunda forma fundamental en una base ortonormal del espacio tangente. Las direcciones principales son los vectores propios correspondientes.
De manera similar, si M es una hipersuperficie en una variedad de Riemann N, entonces las curvaturas principales son los valores propios de su segunda forma fundamental. Si k1, ..., kn son las n curvaturas principales en un punto p ∈ M y X1, . .., Xn son los vectores propios ortonormales correspondientes (direcciones principales), entonces la curvatura seccional de M en p viene dada por
para todos los con .
Clasificación de puntos en una superficie
- En los puntos elípticos, ambas curvaturas principales tienen el mismo signo y la superficie es localmente convexa.
- En los puntos umbilicales, ambas curvaturas principales son iguales y cada vector tangente puede considerarse una dirección principal. Este caso suele darse en puntos aislados.
- En los puntos hiperbólicos, las curvaturas principales tienen signos opuestos y la superficie tendrá localmente forma de silla de montar.
- En los puntos parabólicos, una de las curvaturas principales es cero. Los puntos parabólicos generalmente se encuentran en una curva que separa las regiones elípticas e hiperbólicas.
- En los puntos umbilicales planos ambas curvaturas principales son cero. Una superficie genérica no contendrá puntos umbilicales planos. La silla de mono es una superficie con un plano umbilical aislado.
| k1 | ||||
|---|---|---|---|---|
| < 0 | = 0 | > 0 | ||
| k2 | < 0 | Elipsoide cóncavo | Cilindro cóncavo | Superficie hiperboloide |
| = 0 | Cilindro cóncavo | Plano | Cilindro convexo | |
| > 0 | Superficie hiperboloide | Cilindro convexo | Elipsoide convexo | |
Líneas de curvatura
Las líneas de curvatura son curvas que siempre son tangentes a una dirección principal (son curvas integrales para los campos de dirección principal). Habrá dos líneas de curvatura a través de cada punto no umbilical, que se cruzan en ángulo recto.
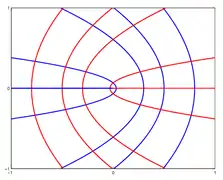
En las proximidades de un punto umbilical, las líneas de curvatura suelen formar una de tres configuraciones: estrella, limón y monstar (derivada de lemon-star).[2] Estos puntos también se llaman puntos umbílicos darbouxianos (D1, D2, D3) en honor a Jean Gaston Darboux, el primero en realizar un estudio sistemático en el vol. 4, p 455, de sus Leçons (1896).
- Configuraciones de líneas de curvatura cerca de puntos umbilicales:
 Limón - D1
Limón - D1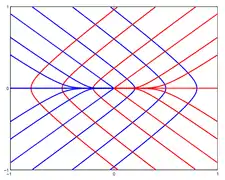 Monstar - D2
Monstar - D2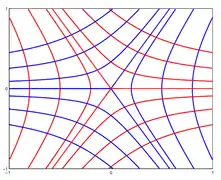 Estrella - D3
Estrella - D3
En estas figuras, las curvas rojas son las líneas de curvatura de una familia de direcciones principales y las curvas azules de la otra.
Cuando una línea de curvatura tiene un extremo local de la misma curvatura principal, entonces la curvatura tiene un punto de cresta. Estos puntos de cresta forman curvas en la superficie llamadas crestas. Las curvas de la cresta pasan por los puntos umbilicales. Para el patrón de estrella, 3 o 1 líneas de cresta pasan a través del punto umbilical, para el patrón de estrella y limón solo pasa una línea de cresta.[3]
Aplicaciones
Las direcciones de curvatura principales junto con la normal de la superficie definen un marco de orientación 3D en un punto de la superficie. Por ejemplo, en el caso de una superficie cilíndrica, al tocar físicamente o al observarla visualmente, se sabe que en una dirección específica la superficie es plana (paralela al eje del cilindro) y, por lo tanto, se puede fijar la orientación de la superficie. La implicación de dicho marco de orientación en cada punto de la superficie significa que cualquier rotación de las superficies en el tiempo puede determinarse simplemente considerando el cambio en los marcos de orientación correspondientes. Esto ha dado como resultado algoritmos de estimación de movimiento y segmentación de puntos de superficie única en visión por computadora.[4]
Véase también
Referencias
- Surface Curvature
- Berry, M. V.; Hannay, J. H. (1977). «Umbilic points on Gaussian random surfaces». Journal of Physics A 10 (11): 1809-21. Bibcode:1977JPhA...10.1809B. S2CID 55230556. doi:10.1088/0305-4470/10/11/009.
- Porteous, I. R. (1994). Geometric Differentiation. Cambridge University Press. ISBN 0-521-39063-X.
- Perera, S.; Barnes, N. (November 2013). «1-Point Rigid Motion Estimation and Segmentation with a RGB-D Camera». 2013 International Conference on Digital Image Computing: Techniques and Applications (DICTA). pp. 1-8. ISBN 978-1-4799-2126-3. S2CID 15915653. doi:10.1109/DICTA.2013.6691469.
Bibliografía
- Darboux, Gaston (1896) [1887]. Leçons sur la théorie génerale des surfaces. Gauthier-Villars.
- Guggenheimer, Heinrich (1977). «Chapter 10. Surfaces». Differential Geometry. Dover. ISBN 0-486-63433-7.
- Kobayashi, Shoshichi; Nomizu, Katsumi (1996). Foundations of Differential Geometry, Vol. 2 (New edición). Wiley-Interscience. ISBN 0-471-15732-5.
- Spivak, Michael (1999). A Comprehensive introduction to differential geometry (Volume 3). Publish or Perish. ISBN 0-914098-72-1.
- Sotomayor, J. (1993). O elipsóide de Monge= Revista Matemática Universitária 15. pp. 33-47.
- Sotomayor, J. (2007). «El elipsoide de Monge y las líneas de curvatura». Materials Matemàtics 01: 1-25.