Plano normal (geometría)
Un plano normal es cualquier plano que contenga el vector normal de una sperficie en un punto dado.
El plano normal también se refiere al plano que es perpendicularidad al tangent vector de un curva; (este plano también contiene el vector normal) ver Fórmulas de Frenet-Serret.
Sección normal
La sección normal de un surface en un point particular es el curva producido por el intersection de esa superficie con un plano normal.[1][2][3]
El curvatura de la sección normal se llama marco de Darboux.
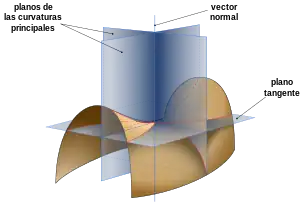
Si la superficie tiene forma de arco o cilindro, el máximo y el mínimo de estas curvaturas son la curvaturas principales.
Si la superficie es saddle shaped los máximos de ambos lados son las curvaturas principales.
El producto de las curvaturas principales es el Curvatura de Gauss de la superficie (negativo para superficies en forma de silla de montar).
La media de las curvaturas principales es la curvatura media de la superficie; si (y solo si) la curvatura media es cero, la superficie se denomina superficie minimal.
Véase también
- Earth normal section
- Normal bundle
- Marco de Darboux
- Osculating plane
- Curvaturas principales
- Tangente (geometría)
Referencias
- Ruane, Irving Adler, with diagrams by Ruth Adler ; introduction to the Dover edition by Peter (2012). A new look at geometry (Dover edición). Mineola, N.Y.: Dover Publications. p. 273. ISBN 978-0486498515.
- Irving Adler (30 de agosto de 2013). A New Look at Geometry. p. 273. ISBN 9780486320496. Consultado el 1 de abril de 2016.
- Alfred Gray (29 de diciembre de 1997). Modern Differential Geometry of Curves and Surfaces with Mathematica, Second .... p. 365. ISBN 9780849371646. Consultado el 1 de abril de 2016.