Teoría de la computación

Esta teoría provee modelos matemáticos que formalizan el concepto de computadora o algoritmo de manera suficientemente simplificada y general para que se puedan analizar sus capacidades y limitaciones. Algunos de estos modelos juegan un papel central en varias aplicaciones de las ciencias de la computación, incluyendo procesamiento de texto, compiladores, diseño de hardware e inteligencia artificial.

Existen muchos otros tipos de autómatas como las máquinas de acceso aleatorio, autómatas celulares, máquinas ábaco y las máquinas de estado abstracto; sin embargo en todos los casos se ha mostrado que estos modelos no son más generales que la máquina de Turing, pues la máquina de Turing tiene la capacidad de simular cada uno de estos autómatas. Esto da lugar a que se piense en la máquina de Turing como el modelo universal de computadora.

Gramática	Idiomas	Autómatas	Reglas de producción (restricciones)
Tipo-0	Enumerable recursivamente	Máquina de Turing	${\displaystyle \alpha \rightarrow \beta }$ (sin restricciones)
Tipo-1	Sensibles al contexto	Máquina de Turing no determinista de límites lineales	${\displaystyle \alpha A\beta \rightarrow \alpha \gamma \beta }$
Tipo-2	sin contexto	No-determinista Autómata con pila	${\displaystyle A\rightarrow \gamma }$
Tipo-3	Regular	Autómata finito	${\displaystyle A\rightarrow a}$ and ${\displaystyle A\rightarrow aB}$

Esta teoría explora los límites de la posibilidad de solucionar problemas mediante algoritmos. Gran parte de las ciencias computacionales están dedicadas a resolver problemas de forma algorítmica, de manera que el descubrimiento de problemas imposibles es una gran sorpresa. La teoría de la computabilidad es útil para no tratar de resolver algorítmicamente estos problemas, ahorrando así tiempo y esfuerzo.

Los problemas se clasifican en esta teoría de acuerdo a su grado de imposibilidad:

• Los computables son aquellos para los cuales sí existe un algoritmo que siempre los resuelve cuando hay una solución y además es capaz de distinguir los casos que no la tienen. También se les conoce como decidibles, resolubles o recursivos.
• Los semicomputables son aquellos para los cuales hay un algoritmo que es capaz de encontrar una solución si es que existe, pero ningún algoritmo que determine cuando la solución no existe (en cuyo caso el algoritmo para encontrar la solución entraría a un bucle infinito). El ejemplo clásico por excelencia es el problema de la parada. A estos problemas también se les conoce como listables, recursivamente enumerables o reconocibles, porque si se enlistan todos los casos posibles del problema, es posible reconocer a aquellos que sí tienen solución.
• Los incomputables son aquellos para los cuales no hay ningún algoritmo que los pueda resolver, no importando que tengan o no solución. El ejemplo clásico por excelencia es el problema de la implicación lógica, que consiste en determinar cuándo una proposición lógica es un teorema; para este problema no hay ningún algoritmo que en todos los casos pueda distinguir si una proposición o su negación es un teorema.

Hay una versión más general de esta clasificación, donde los problemas incomputables se subdividen a su vez en problemas más difíciles que otros. La herramienta principal para lograr estas clasificaciones es el concepto de reducibilidad: Un problema ${\displaystyle A}$ se reduce al problema ${\displaystyle B}$ si bajo la suposición de que se sabe resolver el problema ${\displaystyle B}$ es posible resolver al problema ${\displaystyle A}$; esto se denota por ${\displaystyle A\leq _{t}B}$, e informalmente significa que el problema ${\displaystyle A}$ no es más difícil de resolver que el problema ${\displaystyle B}$. Por ejemplo, bajo la suposición de que una persona sabe sumar, es muy fácil enseñarle a multiplicar haciendo sumas repetidas, de manera que multiplicar se reduce a sumar.

Conjunto de inclusiones descritas por la jerarquía de Chomsky

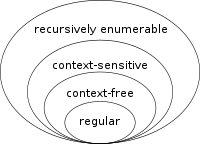
La teoría del lenguaje es una rama de las matemáticas que se ocupa de describir los lenguajes como un conjunto de operaciones sobre un alfabeto. Está estrechamente relacionada con la teoría de autómatas, ya que éstos se utilizan para generar y reconocer lenguajes formales. Existen varias clases de lenguajes formales, cada una de las cuales permite una especificación del lenguaje más compleja que la anterior, es decir, la jerarquía de Chomsky,[5] y cada una correspondiente a una clase de autómatas que la reconoce. Dado que los autómatas se utilizan como modelos para la computación, los lenguajes formales son el modo preferido de especificación para cualquier problema que deba ser computado.

Aun cuando un problema sea computable, puede que no sea posible resolverlo en la práctica si se requiere mucha memoria o tiempo de ejecución. La teoría de la complejidad computacional estudia las necesidades de memoria, tiempo y otros recursos computacionales para resolver problemas; de esta manera es posible explicar por qué unos problemas son más difíciles de resolver que otros. Uno de los mayores logros de esta rama es la clasificación de problemas, similar a la tabla periódica, de acuerdo a su dificultad. En esta clasificación los problemas se separan por clases de complejidad.

Esta teoría tiene aplicación en casi todas las áreas de conocimiento donde se desee resolver un problema computacionalmente, porque los investigadores no solo desean utilizar un método para resolver un problema, sino utilizar el más rápido. La teoría de la complejidad computacional también tiene aplicaciones en áreas como la criptografía, donde se espera que descifrar un código secreto sea un problema muy difícil a menos que se tenga la contraseña, en cuyo caso el problema se vuelve fácil.

Para analizar cuánto tiempo y espacio requiere un algoritmo determinado, los informáticos expresan el tiempo o el espacio necesarios para resolver el problema en función del tamaño del problema de entrada. Por ejemplo, encontrar un número concreto en una larga lista de números se hace más difícil a medida que la lista de números aumenta de tamaño. Si decimos que hay "n" números en la lista, entonces, si la lista no está ordenada o indexada de alguna manera, puede que tengamos que mirar todos los números para encontrar el número que buscamos. Por tanto, para resolver este problema, el ordenador debe realizar un número de pasos que crece linealmente con el tamaño del problema.

Para simplificar este problema, los informáticos han adoptado la notación Big O, que permite comparar funciones de forma que no sea necesario considerar aspectos particulares de la construcción de una máquina, sino sólo el comportamiento asintótico a medida que los problemas se hacen grandes. Así, en nuestro ejemplo anterior, podríamos decir que el problema requiere ${\displaystyle O(n)}$ pasos para resolverse.

Quizás el problema abierto más importante en toda la informática es la cuestión de si una cierta clase amplia de problemas denotada NP puede resolverse eficientemente. Esto se discute más a fondo en Clases de complejidad P y NP, y Clases de complejidad P y NP es uno de los siete Problemas del Premio del Milenio enunciados por el Clay Mathematics Institute en 2000. La Descripción Oficial del Problema fue dada por el ganador del Premio Turing Stephen Cook.