Interpolación multivariable
En análisis numérico, la interpolación multivariable o la interpolación espacial es la interpolación sobre funciones de más de una variable.
La función a interpolar se conoce en puntos determinados y el problema de la interpolación consistirá en dar valores en puntos arbitrarios .
Cuadrícula regular
Para los valores de una función conocida en una cuadrícula regular (que tienen separación predeterminada, no necesariamente uniforme), están disponibles los siguientes métodos.
Cualquier dimensión
2 dimensiones
- Interpolación bilineal
- Interpolación bicúbica
- Superficie de Bézier
- Remuestreo de Lanczos
- Triangulación de Delaunay
- Interpolación spline
- Vecino natural
- Krigeaje
- Ponderación inversa a la distancia
Bitmap resampling es la aplicación de interpolación multivariable en 2D al procesamiento de imágenes.
Tres de los métodos aplicados sobre el mismo conjunto de datos, 16 valores situados en los puntos negros. Los colores representan los valores interpolados.
Vecino más cercano
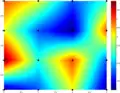Bilineal
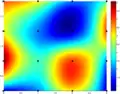Bicúbica
Véase puntos de Padua, para interpolación polinómica en dos variables.
3 dimensiones
- Interpolación trilineal
- Interpolación tricúbica
Véase también bitmap resampling.
Cuadrícula irregular (datos dispersos)
Todos los esquemas definidos para datos dispersos en una cuadrícula irregular deben trabajar en una malla regular, por lo general reduciéndose a otro método conocido.
- Interpolación por el vecino más cercano
- Vecino natural basado en red irregular de triángulos
- interpolación lineal basada en red irregular de triángulos (un tipo de función lineal a trozos)
- Ponderación inversa a la distancia
- Krigeaje
- Función de base radial
- Spline de placa delgada
- Spline poliarmónica (el spline de placa delgada es un caso especial de la spline poliarmónica)
- Spline por mínimos cuadrados
Referencias
Enlaces externos
- Example C++ code for several 1D, 2D and 3D spline interpolations (including Catmull-Rom splines).
- Multi-dimensional Hermite Interpolation and Approximation, Prof. Chandrajit Bajaja, Purdue University
| Control de autoridades |
|
|---|
Datos: Q6334079